-
Notifications
You must be signed in to change notification settings - Fork 128
nurbs.scad
B-Splines and Non-uniform Rational B-Splines (NURBS) are a way to represent smooth curves and smoothly curving surfaces with a set of control points. The curve or surface is defined by the control points and a set of "knot" points. The NURBS can be "clamped" in which case the curve passes through the first and last point, or they can be "closed" in which case the first and last point are coincident. Also possible are "open" curves which do not necessarily pass through any of their control points. Unlike Bezier curves, a NURBS can have an unlimited number of control points and changes to the control points only affect the curve locally.
To use, add the following lines to the beginning of your file:
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
-
-
nurbs_curve()– Computes one more more points on a NURBS curve. [Path] -
debug_nurbs()– Shows a NURBS curve and its control points, knots and weights [Geom]
-
-
-
is_nurbs_patch()– Returns true if the given item looks like a NURBS patch. -
nurbs_patch_points()– Computes specifies point(s) on a NURBS surface patch -
nurbs_vnf()– Generates a (possibly non-manifold) VNF for a single NURBS surface patch. [VNF]
-
Synopsis: Computes one more more points on a NURBS curve. [Path]
Topics: NURBS Curves
See Also: debug_nurbs()
Usage:
- pts = nurbs_curve(control, degree, splinesteps, [mult=], [weights=], [type=], [knots=]);
- pts = nurbs_curve(control, degree, u=, [mult=], [weights=], [type=], [knots=]);
Description:
Compute the points specified by a NURBS curve. You specify the NURBS by supplying the control points, knots and weights. and knots.
Only the control points are required. The knots and weights default to uniform, in which case you get a uniform B-spline.
You can specify endpoint behavior using the type parameter. The default, "clamped", gives a curve which starts and
ends at the first and last control points and moves in the tangent direction to the first and last control point segments.
If you request an "open" spline you get a curve which starts somewhere in the middle of the control points.
Finally, a "closed" curve is a one that starts where it ends. Note that each of these types of curve require
a different number of knots.
The control points are the most important control over the shape of the curve. You must have at least p+1 control points for clamped and open NURBS. Unlike a bezier, there is no maximum number of control points. A single NURBS is more like a bezier path than like a single bezier spline.
A NURBS or B-spline is a curve made from a moving average of several Bezier curves. The knots specify when one Bezier fades
away to be replaced by the next one. At generic points, the curves are differentiable, but by increasing knot multiplicity, you
can decrease smoothness, or even produce a sharp corner. The knots must be an ascending sequence of values, but repeating values
is OK and controls the smoothness at the knots. The easiest way to specify the knots is to take the default of uniform knots,
and simply set the multiplicity to create repeated knots as needed. The total number of knots is then the sum of the multiplicity
vector. Alternatively you can simply list the knots yourself. Note that regardless of knot values, the domain of evaluation
for u is always the interval [0,1], and it will be scaled to give the entire valid portion of the curve you have chosen.
If you give both a knot vector and multiplicity then the multiplicity vector is appled to the provided knots.
For an open spline the number of knots must be len(control)+p+1. For a clamped spline the number of knots is len(control)-p+1,
and for a closed spline you need len(control)+1 knots. If you are using the default uniform knots then the way to
ensure that you have the right number is to check that sum(mult) is either not set or equal to the correct value.
You can use this function to evaluate the NURBS at u, which can be a single point or a list of points. You can also
use it to evaluate the NURBS over its entire domain by giving a splinesteps value. This specifies the number of segments
to use between each knot and guarantees a point exactly at each knot. This may be important if you set the knot multiplicity
to the degree somewhere in your curve, which creates a corner at the knot, because it guarantees a sharp corner regardless
of the number of points.
Arguments:
| By Position | What it does |
|---|---|
control |
list of control points in any dimension |
degree |
degree of NURBS |
splinesteps |
evaluate whole spline with this number of segments between each pair of knots |
| By Name | What it does |
|---|---|
u |
list of values or range in the interval [0,1] where the NURBS should be evaluated |
mult |
list of multiplicities of the knots. Default: all 1 |
weights |
vector whose length is the same as control giving weights at each control point. Default: all 1 |
type |
One of "clamped", "closed" or "open" to define end point handling of the spline. Default: "clamped" |
knots |
List of knot values. Default: uniform |
Example 1: Compute some points and draw a curve and also some specific points:
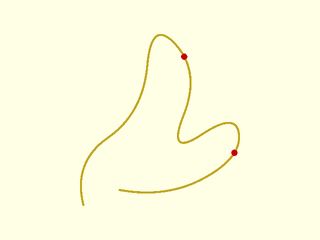
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
control = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
curve = nurbs_curve(control,2,splinesteps=16);
pts = nurbs_curve(control,2,u=[0.4,0.8]);
stroke(curve);
color("red")move_copies(pts) circle(r=1.5,$fn=16);
Example 2: Compute NURBS points and make a polygon

include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
control = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
curve = nurbs_curve(control,2,splinesteps=16,type="closed");
polygon(curve);
Example 3: Simple quadratic uniform clamped b-spline with some points computed using splinesteps.
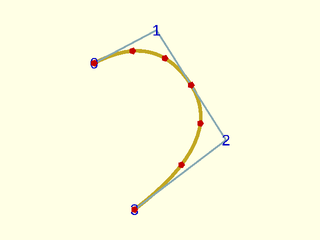
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[13,43],[30,52],[49,22],[24,3]];
debug_nurbs(pts,2);
npts = nurbs_curve(pts, 2, splinesteps=3);
color("red")move_copies(npts) circle(r=1);
Example 4: Simple quadratic uniform clamped b-spline with some points computed using the u parameter. Note that a uniform u parameter doesn't necessarily sample the curve uniformly.
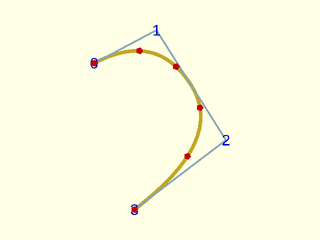
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[13,43],[30,52],[49,22],[24,3]];
debug_nurbs(pts,2);
npts = nurbs_curve(pts, 2, u=[0:.2:1]);
color("red")move_copies(npts) circle(r=1);
Example 5: Same control points, but cubic
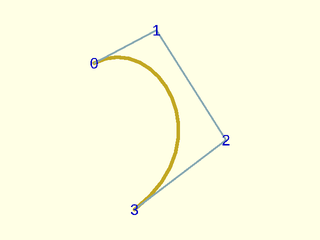
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[13,43],[30,52],[49,22],[24,3]];
debug_nurbs(pts,3);
Example 6: Same control points, quadratic and closed
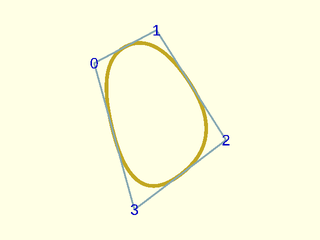
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[13,43],[30,52],[49,22],[24,3]];
debug_nurbs(pts,2,type="closed");
Example 7: Same control points, cubic and closed
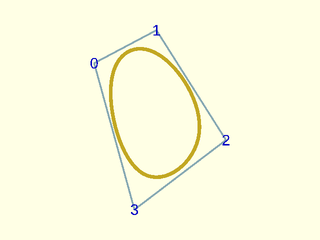
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[13,43],[30,52],[49,22],[24,3]];
debug_nurbs(pts,3,type="closed");
Example 8: Ten control points, quadratic, clamped
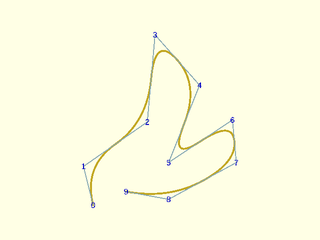
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,2);
Example 9: Same thing, degree 4
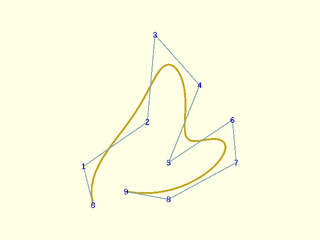
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,4);
Example 10: Same control points, degree 2, open. Note it doesn't reach the ends
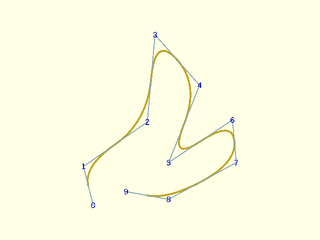
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,2, type="open");
Example 11: Same control points, degree 4, open. Note it starts farther from the ends
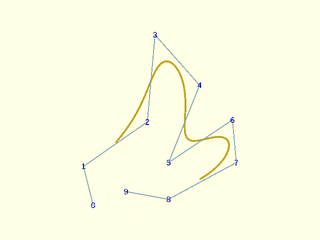
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,4,type="open");
Example 12: Same control points, degree 2, closed
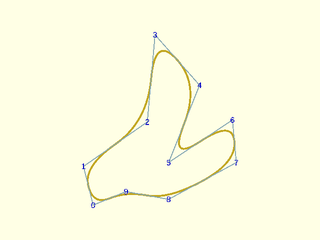
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,2,type="closed");
Example 13: Same control points, degree 4, closed
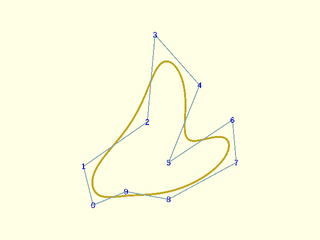
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,4,type="closed");
Example 14: Adding weights
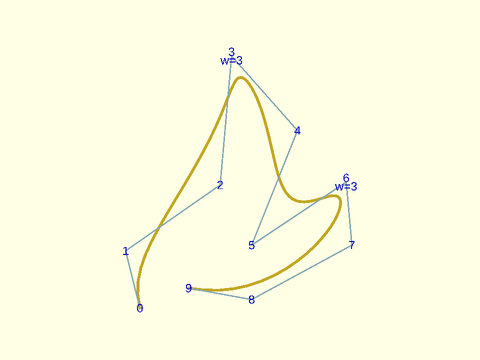
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
weights = [1,1,1,3,1,1,3,1,1,1];
debug_nurbs(pts,4,type="clamped",weights=weights);
Example 15: Using knot multiplicity with quadratic clamped case. Knot count is len(control)-degree+1 = 9. The multiplicity 2 knot creates a corner for a quadratic.
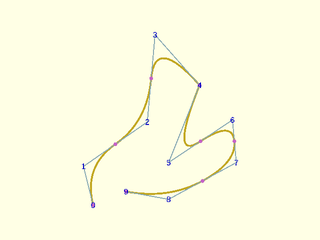
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
mult = [1,1,1,2,1,1,1,1];
debug_nurbs(pts,2,mult=mult,show_knots=true);
Example 16: Using knot multiplicity with quadratic clamped case. Two knots of multiplicity 2 gives two corners
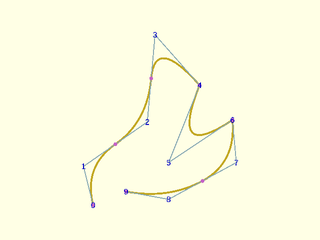
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
mult = [1,1,1,2,2,1,1];
debug_nurbs(pts,2,mult=mult,show_knots=true);
Example 17: Using knot multiplicity with cubic clamped case. Knot count is now 8. We need multiplicity equal to degree (3) to create a corner.
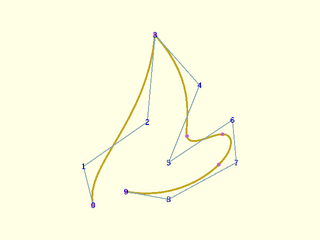
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
mult = [1,3,1,1,1,1];
debug_nurbs(pts,3,mult=mult,show_knots=true);
Example 18: Using knot multiplicity with cubic closed case. Knot count is now len(control)+1=11. Here are three corners.
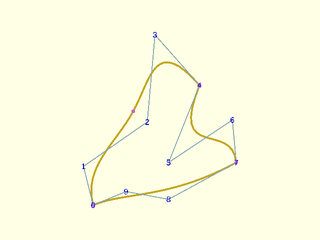
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
mult = [1,3,1,3,3];
debug_nurbs(pts,3,mult=mult,type="closed",show_knots=true);
Example 19: Explicitly specified knots only change the quadratic clamped curve slightly. Knot count is len(control)-degree+1 = 9.
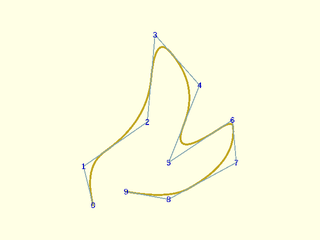
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
knots = [0,1,3,5,9,13,14,19,21];
debug_nurbs(pts,2,knots=knots);
Example 20: Combining explicit knots with mult for the quadratic curve to add a corner
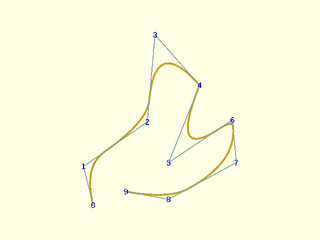
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
knots = [0,1,3,9,13,14,19,21];
mult = [1,1,1,2,1,1,1,1];
debug_nurbs(pts,2,knots=knots,mult=mult);
Example 21: Directly repeating a knot in the knot list to create a corner for a cubic spline
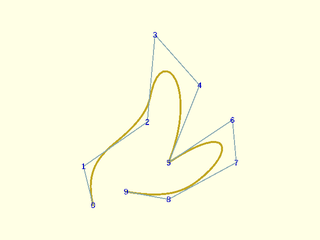
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
knots = [0,1,3,13,13,13,19,21];
debug_nurbs(pts,3,knots=knots);
Example 22: Open cubic spline with explicit knots
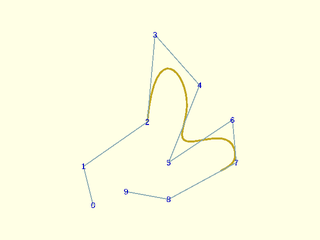
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
knots = [0,1,3,13,13,13,19,21,27,28,29,40,42,44];
debug_nurbs(pts,3,knots=knots,type="open");
Example 23: Closed quintic spline with explicit knots
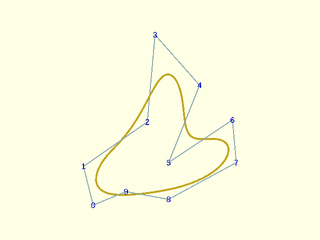
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
knots = [0,1,3,13,13,13,19,21,27,28,33];
debug_nurbs(pts,5,knots=knots,type="closed");
Example 24: Closed quintic spline with explicit knots and weights
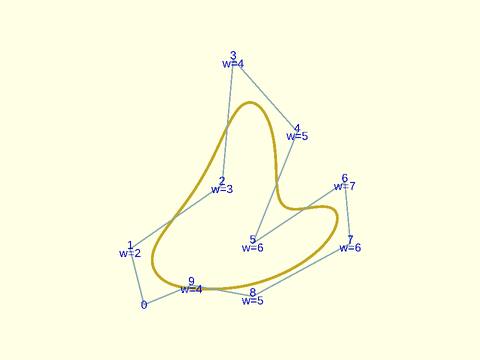
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
weights = [1,2,3,4,5,6,7,6,5,4];
knots = [0,1,3,13,13,13,19,21,27,28,33];
debug_nurbs(pts,5,knots=knots,weights=weights,type="closed");
Example 25: Circular arcs are possible with NURBS. This example gives a semi-circle
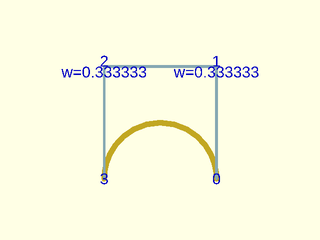
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
control = [[1,0],[1,2],[-1,2],[-1,0]];
w = [1,1/3,1/3,1];
debug_nurbs(control, 3, weights=w, width=0.1, size=.2);
Example 26: Gluing two semi-circles together gives a whole circle. Note that this is a clamped not closed NURBS. The interface uses a knot of multiplicity 3 where the clamped ends of the semi-circles meet.
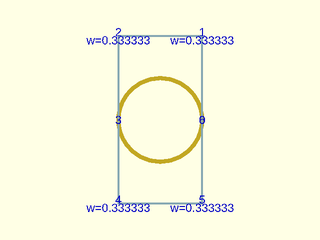
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
control = [[1,0],[1,2],[-1,2],[-1,0],[-1,-2],[1,-2],[1,0]];
w = [1,1/3,1/3,1,1/3,1/3,1];
debug_nurbs(control, 3, splinesteps=16,weights=w,mult=[1,3,1],width=.1,size=.2);
Example 27: Circle constructed with type="closed"
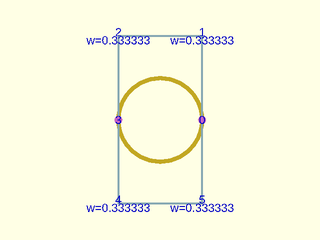
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
control = [[1,0],[1,2],[-1,2],[-1,0],[-1,-2],[1,-2]];
w = [1,1/3,1/3,1,1/3,1/3];
debug_nurbs(control, 3, splinesteps=16,weights=w,mult=[1,3,3],width=.1,size=.2,type="closed",show_knots=true);
Synopsis: Shows a NURBS curve and its control points, knots and weights [Geom]
See Also: nurbs_curve()
Usage:
- debug_nurbs(control, degree, [width], [splinesteps=], [type=], [mult=], [knots=], [size=], [show_weights=], [show_knots=], [show_idx=]);
Description:
Displays a 2D or 3D NURBS and the associated control points to help debug NURBS curves. You can display the control point indices and weights, and can also display the knot points.
Arguments:
| By Position | What it does |
|---|---|
control |
control points for NURBS |
degree |
degree of NURBS |
splinesteps |
number of segments between each pair of knots. Default: 16 |
width |
width of the line. Default: 1 |
size |
size of text annotations. Default: 3 times the width |
mult |
multiplicity vector for NURBS |
weights |
weight vector for NURBS |
type |
NURBS type, one of "clamped", "open" or "closed". Default: "clamped" |
show_index |
if true then display index of each control point vertex. Default: true |
show_weights |
if true then display any non-unity weights. Default: true if weights vector is supplied, false otherwise |
show_knots |
If true then show the knots on the spline curve. Default: false |
Example 1: The default display includes the control point polygon with its vertices numbered, and the NURBS curve
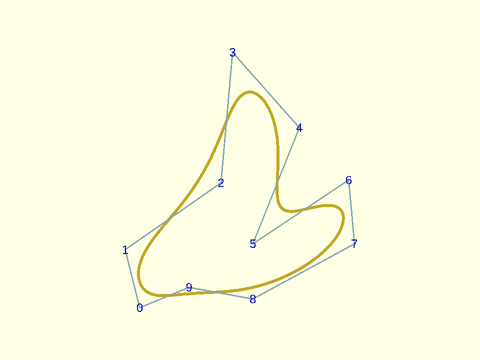
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,4,type="closed");
Example 2: If you want to see the knots set show_knots=true:
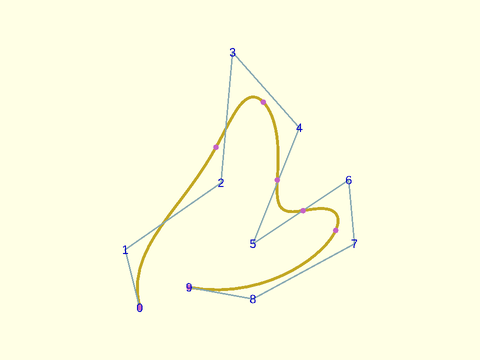
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
debug_nurbs(pts,4,type="clamped",show_knots=true);
Example 3: Non-unity weights are displayed if you give a weight vector
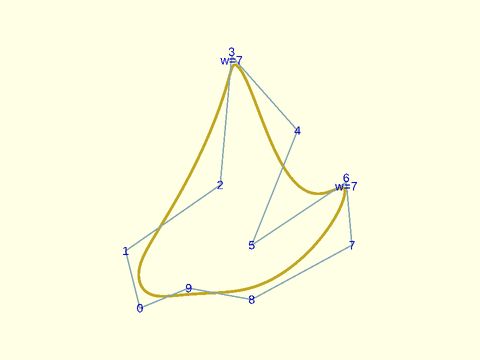
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
pts = [[5,0],[0,20],[33,43],[37,88],[60,62],[44,22],[77,44],[79,22],[44,3],[22,7]];
weights = [1,1,1,7,1,1,7,1,1,1];
debug_nurbs(pts,4,type="closed",weights=weights);
Synopsis: Returns true if the given item looks like a NURBS patch.
Topics: NURBS Patches, Type Checking
Usage:
- bool = is_nurbs_patch(x);
Description:
Returns true if the given item looks like a NURBS patch. (a 2D array of 3D points.)
Arguments:
| By Position | What it does |
|---|---|
x |
The value to check the type of. |
Synopsis: Computes specifies point(s) on a NURBS surface patch
Topics: NURBS Patches
See Also: nurbs_vnf(), nurbs_curve()
Usage:
- pointgrid = nurbs_patch_points(patch, degree, [splinesteps], [u=], [v=], [weights=], [type=], [mult=], [knots=]);
Description:
Sample a NURBS patch on a point set. If you give splinesteps then it will sampled uniformly in the spline parameter between the knots, ensuring that a sample appears at every knot. If you instead give u and v then the values at those points in parameter space will be returned. The various NURBS parameters can all be single values, if the NURBS has the same parameters in both directions, or pairs listing the value for the two directions.
Arguments:
| By Position | What it does |
|---|---|
patch |
rectangular list of control points in any dimension |
degree |
a scalar or 2-vector giving the degree of the NURBS in the two directions |
splinesteps |
a scalar or 2-vector giving the number of segments between each knot in the two directions |
| By Name | What it does |
|---|---|
u |
evaluation points in the u direction of the patch |
v |
evaluation points in the v direction of the patch |
mult |
a single list or pair of lists giving the knot multiplicity in the two directions. Default: all 1 |
knots |
a single list of pair of lists giving the knot vector in each of the two directions. Default: uniform |
weights |
a single list or pair of lists giving the weight at each control point in the patch. Default: all 1 |
type |
a single string or pair of strings giving the NURBS type, where each entry is one of "clamped", "open" or "closed". Default: "clamped" |
Example 1: Computing points on a patch using ranges
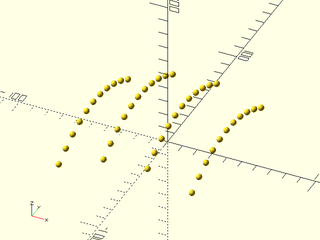
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
pts = nurbs_patch_points(patch, 3, u=[0:.1:1], v=[0:.3:1]);
move_copies(flatten(pts)) sphere(r=2,$fn=16);
Example 2: Computing points using splinesteps
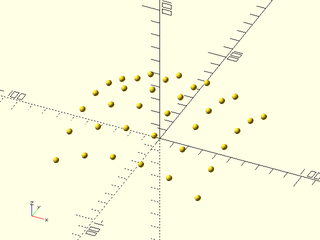
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
pts = nurbs_patch_points(patch, 3, splinesteps=5);
move_copies(flatten(pts)) sphere(r=2,$fn=16);
Synopsis: Generates a (possibly non-manifold) VNF for a single NURBS surface patch. [VNF]
Topics: NURBS Patches
See Also: nurbs_patch_points()
Usage:
- vnf = nurbs_vnf(patch, degree, [splinesteps], [mult=], [knots=], [weights=], [type=], [style=]);
Description:
Compute a (possibly non-manifold) VNF for a NURBS. The input patch must be an array of control points. If weights is given it
must be an array of weights that matches the size of the control points. The style parameter
gives the vnf_vertex_array() style to use. The other parameters may specify the NURBS parameters in the two directions
by giving a single value, which applies to both directions, or a list of two values to specify different values in each direction.
You can specify undef for for a direction to keep the default, such as mult=[undef,v_multiplicity].
Arguments:
| By Position | What it does |
|---|---|
patch |
rectangular list of control points in any dimension |
degree |
a scalar or 2-vector giving the degree of the NURBS in the two directions |
splinesteps |
a scalar or 2-vector giving the number of segments between each knot in the two directions |
| By Name | What it does |
|---|---|
mult |
a single list or pair of lists giving the knot multiplicity in the two directions. Default: all 1 |
knots |
a single list of pair of lists giving the knot vector in each of the two directions. Default: uniform |
weights |
a single list or pair of lists giving the weight at each control point in the. Default: all 1 |
type |
a single string or pair of strings giving the NURBS type, where each entry is one of "clamped", "open" or "closed". Default: "clamped" |
style |
{{vnf_vertex_array ()}} style to use for triangulating the surface. Default: "default" |
Example 1: Quadratic B-spline surface
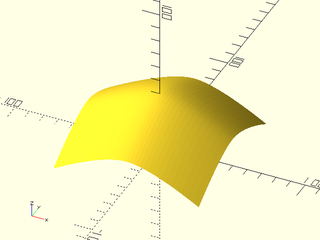
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
vnf = nurbs_vnf(patch, 2);
vnf_polyhedron(vnf);
Example 2: Cubic B-spline surface
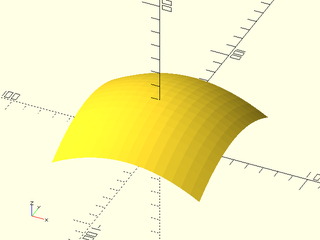
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
vnf = nurbs_vnf(patch, 3);
vnf_polyhedron(vnf);
Example 3: Cubic B-spline surface, closed in one direction
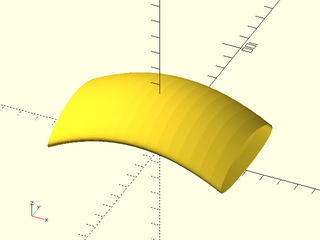
include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
vnf = nurbs_vnf(patch, 3, type=["closed","clamped"]);
vnf_polyhedron(vnf);
Example 4: B-spline surface cubic in one direction, quadratic in the other

include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
];
vnf = nurbs_vnf(patch, [3,2],type=["closed","clamped"]);
vnf_polyhedron(vnf);
Example 5: The sphere can be represented using NURBS

include <BOSL2/std.scad>
include <BOSL2/nurbs.scad>
patch = [
[[0,0,1], [0,0,1], [0,0,1], [0,0,1], [0,0,1], [0,0,1], [0,0,1]],
[[2,0,1], [2,4,1], [-2,4,1], [-2,0,1], [-2,-4,1], [2,-4,1], [2,0,1]],
[[2,0,-1],[2,4,-1],[-2,4,-1],[-2,0,-1],[-2,-4,-1], [2,-4,-1],[2,0,-1]],
[[0,0,-1],[0,0,-1],[0,0,-1], [0,0,-1], [0,0,-1], [0,0,-1], [0,0,-1]]
];
weights = [
[9,3,3,9,3,3,9],
[3,1,1,3,1,1,3],
[3,1,1,3,1,1,3],
[9,3,3,9,3,3,9],
]/9;
vknots = [0, 1/2, 1/2, 1/2, 1];
vnf = nurbs_vnf(patch, 3,weights=weights, knots=[undef,vknots]);
vnf_polyhedron(vnf);
Table of Contents
Function Index
Topics Index
Cheat Sheet
Tutorials
Basic Modeling:
- constants.scad STD
- transforms.scad STD
- attachments.scad STD
- shapes2d.scad STD
- shapes3d.scad STD
- drawing.scad STD
- masks2d.scad STD
- masks3d.scad STD
- distributors.scad STD
- color.scad STD
- partitions.scad STD
- miscellaneous.scad STD
Advanced Modeling:
- paths.scad STD
- regions.scad STD
- skin.scad STD
- vnf.scad STD
- beziers.scad STD
- nurbs.scad
- rounding.scad
- turtle3d.scad
- isosurface.scad
Math:
- math.scad STD
- linalg.scad STD
- vectors.scad STD
- coords.scad STD
- geometry.scad STD
- trigonometry.scad STD
Data Management:
- version.scad STD
- comparisons.scad STD
- lists.scad STD
- utility.scad STD
- strings.scad STD
- structs.scad STD
- fnliterals.scad
Threaded Parts:
Parts:
- ball_bearings.scad
- cubetruss.scad
- gears.scad
- hinges.scad
- joiners.scad
- linear_bearings.scad
- modular_hose.scad
- nema_steppers.scad
- polyhedra.scad
- sliders.scad
- tripod_mounts.scad
- walls.scad
- wiring.scad
STD = Included in std.scad