Pair Adjacent Violators

Overview

An implementation of the Pair Adjacent Violators algorithm for isotonic regression. Written in Kotlin but usable from Java or any other JVM language.

Note this algorithm is also known as "Pool Adjacent Violators".

While not widely known, I've found this algorithm useful in a variety of circumstances, particularly when it comes to calibration of predictive model outputs.

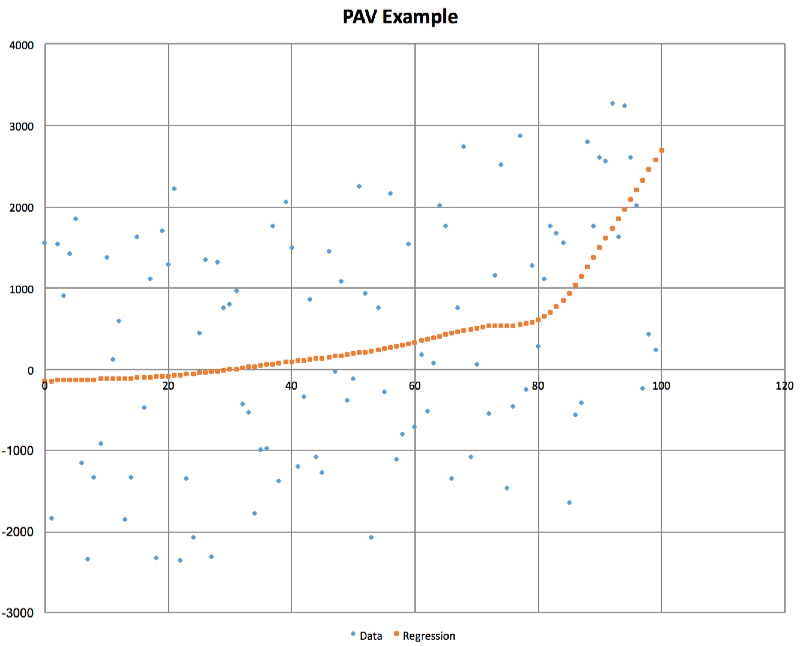
A picture is worth a thousand words:

Features

• Tries to do one thing and do it well with minimal bloat, no external dependencies (other than Kotlin's stdlib)
• Very thorough unit tests, achieving almost 100% mutation test coverage (not including the spline implementation which was ported from Android)
• Employs an isotonic spline algorithm for smooth interpolation
• Fairly efficient implementation without compromizing code readability
• While implemented in Kotlin, works nicely from Java and other JVM languages
• Supports reverse-interpolation

Usage

Adding library dependency

You can use this library by adding a dependency for Gradle, Maven, SBT, Leiningen or another Maven-compatible dependency management system thanks to Jitpack:

Basic usage from Kotlin

import com.github.sanity.pav.PairAdjacentViolators
import com.github.sanity.pav.PairAdjacentViolators.*
// ...
val inputPoints = listOf(Point(3.0, 1.0), Point(4.0, 2.0), Point(5.0, 3.0), Point(8.0, 4.0))
val pav = PairAdjacentViolators(inputPoints)
val interpolator = pav.interpolator()
println("Interpolated: ${interpolator(6.0)}")

Basic usage from Java

import com.github.sanity.pav.*;
import com.github.sanity.pav.PairAdjacentViolators.*;
import kotlin.jvm.functions.*;
import java.util.*;

public class PAVTest {
    public static void main(String[] args) {
        List<Point> points = new LinkedList<>();
        points.add(new Point(0.0, 0.0));
        points.add(new Point(1.0, 1.0));
        points.add(new Point(2.0, 3.0));
        points.add(new Point(3.0, 5.0));
        PairAdjacentViolators pav = new PairAdjacentViolators(points);
        final Function1<Double, Double> interpolator = pav.interpolator();
        for (double x=0; x<3; x+=0.1) {
            System.out.println(x+"\t"+interpolator.invoke(x));
        }
    }
}

Full API documentation

• 1.2.0
• SNAPSHOT (warning: This may take a while to load as it is rebuilt on-demand)

License

Released under the LGPL version 3 by Ian Clarke of Stacks.

Development