You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
The calculation of the hard component of the photonuclear crosssection is done by interpolating tabulated values (see paper by Bugaev et al or one of the PROPOSAL publications for more details).
However, these tabulated values have a limited definition range (10^-7 < v < 1 and 10^2 GeV < E < 10^9 GeV). Outside of this kinematic range, the hard component is set to zero, causing a discontinuity in the differential cross section.
This causes numerical problems in two cases:
For 10^5 MeV
For E = 10^5 MeV, this causes a discontinuity in dEdx and dNdx which is poorly interpolated.
In the direct vicinity of 10^5 MeV, we observe deviations that are 10% at most.
For high energies (E > 10^10 MeV)
For higher energies, the kinematic lower limit in v gets smaller and will at some point start to include the discontinuity in v.
The current integration method in PROPOSAL becomes unstable when integrating over the discontinuity in the differential cross section, which causes oscillations in dEdx and dNdx for high energies:
Above 10^10 MeV, we expect the difference between the interpolated value and the integrated value to be below 1%.
Possible solutions?
The first issue may be solved by avoiding the hard cutoff for E=10^5 MeV
The second issue may be solved by either using a more robust integration method or by solving the hard cutoff in v.
The text was updated successfully, but these errors were encountered:
Jean1995
changed the title
RealPhotonAssumption: Integration and interpolation problems for hard_component
RealPhotonAssumption: Integration and interpolation problems (for hard_component)
Jan 27, 2022
Apparently, the integration problems at high energies (when using small energy cuts such an e_cut of 500 MeV) are also present when not using the hard_component, although they are less severe in this case.
This for example is the dNdx interpolation precision for muons in ice, using an ecut of 500 MeV and using the Zeus parametrization:
We see that we get interpolation problems for energies about 10^10 MeV. If we zoom in on the dNdx values, we see "jumps" in dNdx again:
This could mean that there is some problem with the integration method here, that are also visible without the hard component enabled, but they are amplified if we enable the hard component.
The calculation of the hard component of the photonuclear crosssection is done by interpolating tabulated values (see paper by Bugaev et al or one of the PROPOSAL publications for more details).
However, these tabulated values have a limited definition range (10^-7 < v < 1 and 10^2 GeV < E < 10^9 GeV). Outside of this kinematic range, the hard component is set to zero, causing a discontinuity in the differential cross section.
This causes numerical problems in two cases:
For 10^5 MeV
For E = 10^5 MeV, this causes a discontinuity in dEdx and dNdx which is poorly interpolated.
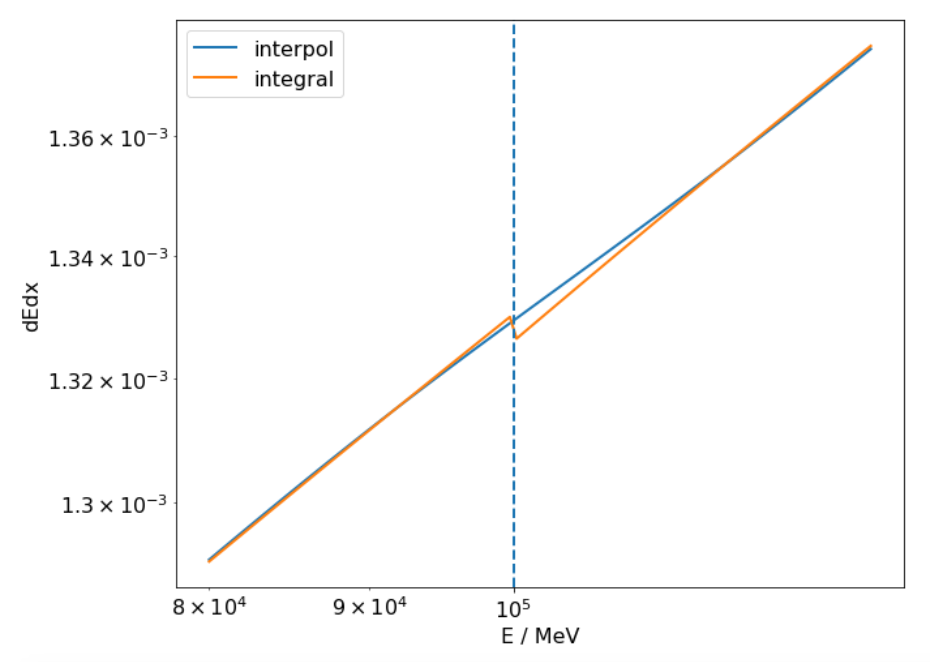
In the direct vicinity of 10^5 MeV, we observe deviations that are 10% at most.
For high energies (E > 10^10 MeV)
For higher energies, the kinematic lower limit in v gets smaller and will at some point start to include the discontinuity in v.
The current integration method in PROPOSAL becomes unstable when integrating over the discontinuity in the differential cross section, which causes oscillations in dEdx and dNdx for high energies:
Above 10^10 MeV, we expect the difference between the interpolated value and the integrated value to be below 1%.
Possible solutions?
The first issue may be solved by avoiding the hard cutoff for E=10^5 MeV
The second issue may be solved by either using a more robust integration method or by solving the hard cutoff in v.
The text was updated successfully, but these errors were encountered: