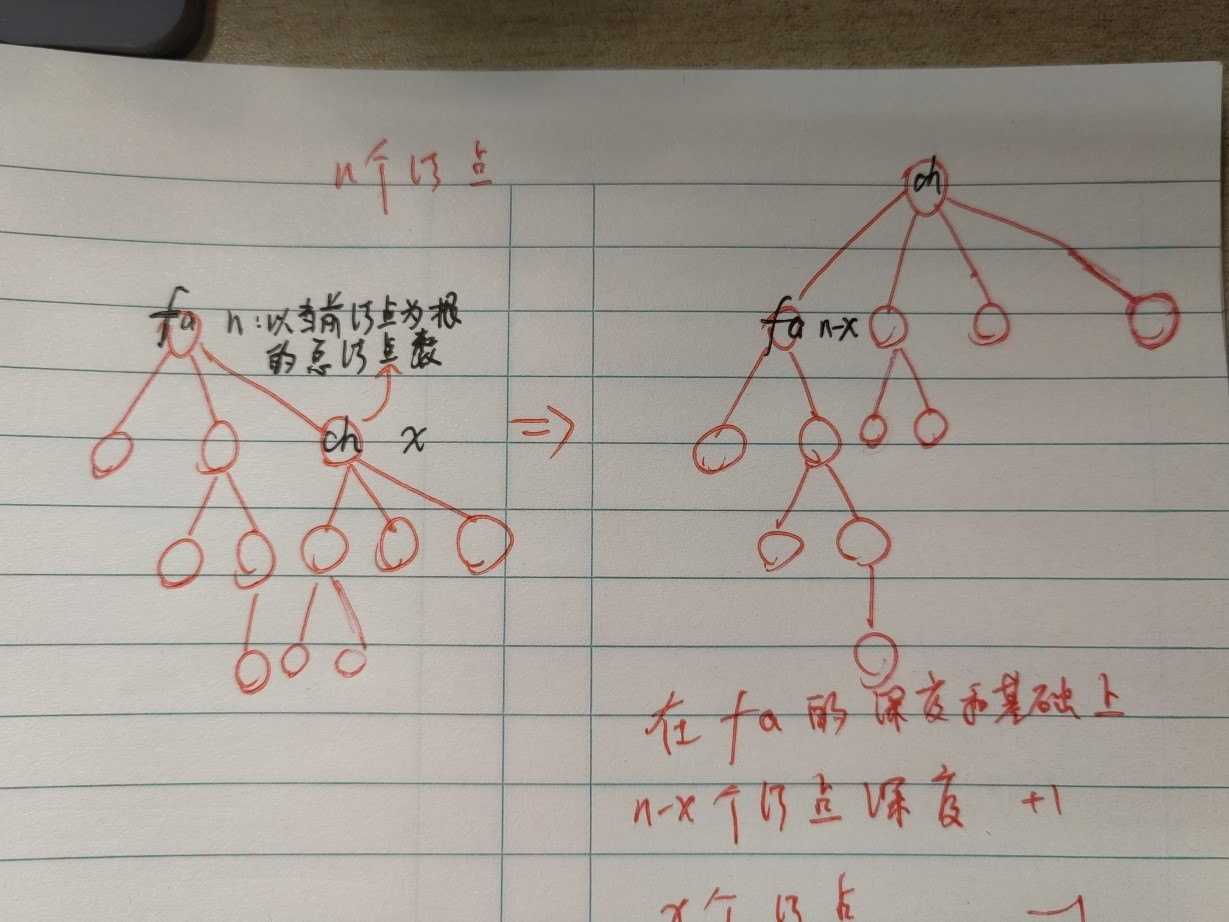
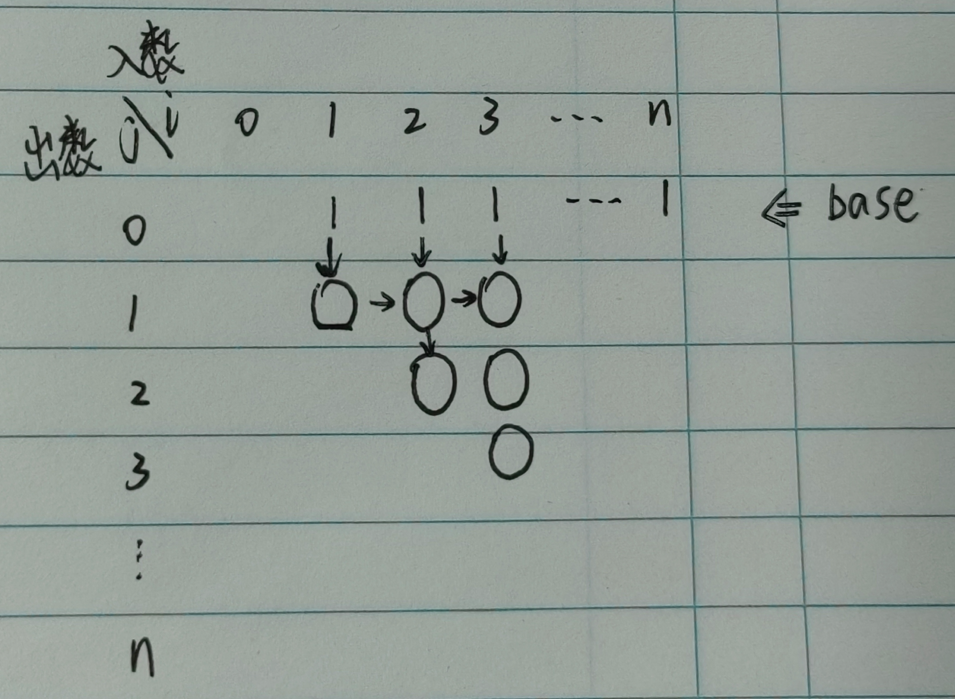
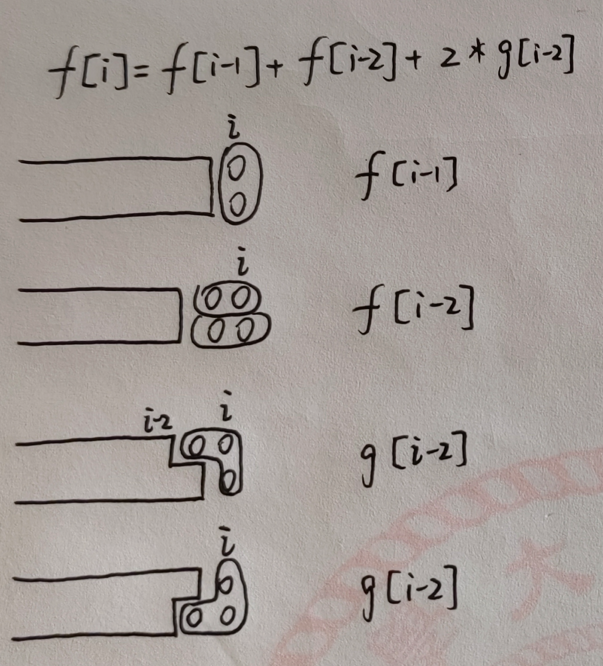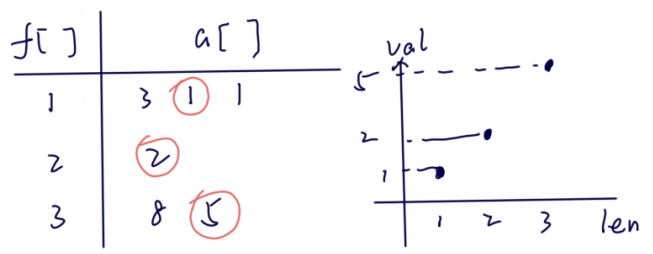计算几何
【二分查找】Bomb
【二分查找】Bomb
【线
-
+
- binary-search
+ dp
上一篇
@@ -802,12 +802,6 @@ 【线
-
- dfs-and-similar
- 下一篇
-
-
-
diff --git a/Algorithm/dfs-and-similar/index.html b/Algorithm/dfs-and-similar/index.html
index b623ad770..ef6f43d59 100644
--- a/Algorithm/dfs-and-similar/index.html
+++ b/Algorithm/dfs-and-similar/index.html
@@ -857,9 +857,9 @@ 【dfs】将
-
+
- data-structure
+ a_template
上一篇
@@ -867,8 +867,8 @@ 【dfs】将
-
- dp
+
+ divide-and-conquer
下一篇
diff --git a/Algorithm/divide-and-conquer/index.html b/Algorithm/divide-and-conquer/index.html
index 6cf89a0ae..2f3819536 100644
--- a/Algorithm/divide-and-conquer/index.html
+++ b/Algorithm/divide-and-conquer/index.html
@@ -425,9 +425,9 @@ 【分治】随机排列
-
+
- a_template
+ dfs-and-similar
上一篇
@@ -435,8 +435,8 @@ 【分治】随机排列
-
- binary-search
+
+ dp
下一篇
diff --git a/Algorithm/dp/index.html b/Algorithm/dp/index.html
index 545026ecf..7bf9f8993 100644
--- a/Algorithm/dp/index.html
+++ b/Algorithm/dp/index.html
@@ -979,9 +979,9 @@ 【状压dp】Avoid K Palindrome
-
+
- dfs-and-similar
+ divide-and-conquer
上一篇
@@ -989,6 +989,12 @@ 【状压dp】Avoid K Palindrome
+
+ data-structure
+ 下一篇
+
+
+
diff --git a/Algorithm/games/index.html b/Algorithm/games/index.html
index 0bca8277d..6500ef3e3 100644
--- a/Algorithm/games/index.html
+++ b/Algorithm/games/index.html
@@ -426,9 +426,9 @@ 【博弈/贪心/交
-
+
- geometry
+ back-end-guide
上一篇
@@ -436,8 +436,8 @@ 【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机
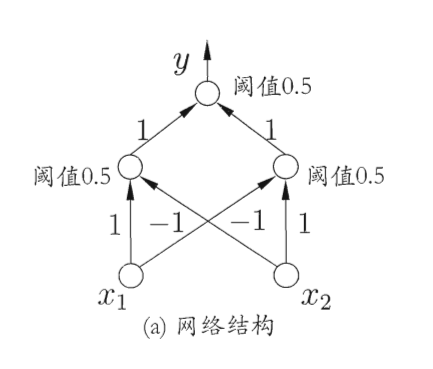
所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+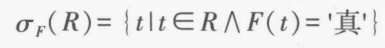
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+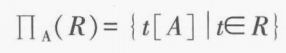
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+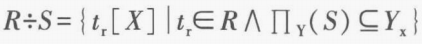
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
前言
学科地位:
主讲教师 学分配额 学科类别 宋歌 3 自发课
成绩组成:
小组作业 个人大作业 40% 60%
教材情况:
课程名称 选用教材 版次 作者 出版社 ISBN 号 神经网络与深度学习 《神经网络与深度学习》 1 邱锡鹏 机械工业出版社 978-7-111-64968-7
学习资源:
为什么要学这门课?
还记得 NJU 的 jyy 老师在上 OS 时说过的一句话,“我们现在学习的微积分是 300 年前的人类智慧结晶,何不再学学 50 年前的人类智慧结晶呢?”印象深刻。当一切都可以用层层嵌套的简单函数模拟时,人类社会必将发生翻天覆地的变化!
会收获什么?
如何学习特征?如何优化调参?为什么要这样做?背后的原理是什么?
概述
绪论
表示学习是什么?与传统的特征工程目的一致,为了得到数据中的更好的特征。不同的是,特征工程中的策略都是可控的方式,而表示学习就是利用深度学习从数据中学习高层的有效特征。
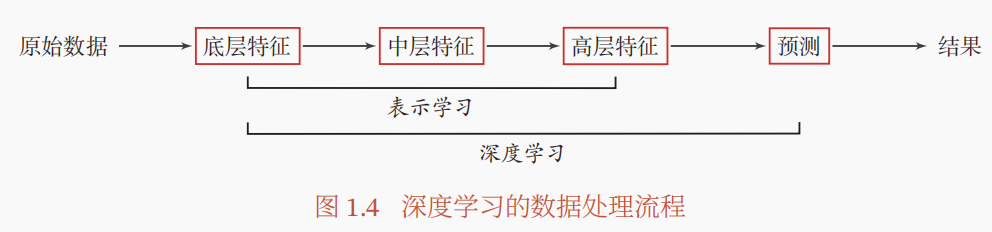
深度学习是什么?我们知道机器学习就是在手动处理完特征后,构建对应的模型 预测输出。而深度学习就是将机器学习的手动特征工程也用模型进行 表示学习 来学习出有效特征,然后继续构建模型 预测输出。如下图所示:
为什么会有深度学习?最简单的一点就是,很多特征我们根本没法定义一种表示规则来表示特征,比如说对于图像,怎么定义复杂的图像的特征呢?比如说对于音频,又怎么定义复杂的音频的特征呢?没办法,我们直接学特征!
神经网络是什么?就是万千模型中的一种,仅此而已。
为什么用神经网络进行深度学习?有了上面对深度学习定义的理解,可以发现其中最具有挑战性的特点就是,模型怎么知道什么才是好特征?什么是不好的特征?神经网络可以很好的解决这个问题。通过由浅到深层层神经元的特征提取,越深的神经元就可以学习更高语义的特征。说的高大上一点就是,神经网络可以很好的解决深度学习中的「贡献度分配」问题。
机器学习概述
数据 → \to → \to → \to
线性模型
学习任务:分类、回归。
学习准则:
- 经验风险最小化:通过 最小化训练集上的损失函数 来学习模型参数。例如:线性回归中的最小二乘损失。
- 结构风险最小化:引入 正则化 来控制模型的复杂度,避免过拟合。
- 最大似然估计:通过 最大化模型在给定数据上的似然函数 来估计模型参数。例如二分类 logistic 和多分类 softmax 中的交叉熵损失。
- 最大后验估计:结合了似然函数和 先验 分布,在贝叶斯框架下估计模型参数。
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
基础神经网络模型
前馈神经网络
卷积神经网络
循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
概率图模型
深度生成模型
强化学习
深度强化学习
个人大作业
- 背景介绍:做好国内外研究现状的调研。
- 项目理解:深入对模型与代码的理解。
- 充分实验:对比实验、验证实验(消融实验)、参数实验(验证模型对不同的参数的敏感性)。
- 项目总结。
]]>
+ 神经网络与深度学习
【线
-
- dfs-and-similar
- 下一篇
-
-
-
diff --git a/Algorithm/dfs-and-similar/index.html b/Algorithm/dfs-and-similar/index.html
index b623ad770..ef6f43d59 100644
--- a/Algorithm/dfs-and-similar/index.html
+++ b/Algorithm/dfs-and-similar/index.html
@@ -857,9 +857,9 @@ 【dfs】将
-
+
- data-structure
+ a_template
上一篇
@@ -867,8 +867,8 @@ 【dfs】将
-
- dp
+
+ divide-and-conquer
下一篇
diff --git a/Algorithm/divide-and-conquer/index.html b/Algorithm/divide-and-conquer/index.html
index 6cf89a0ae..2f3819536 100644
--- a/Algorithm/divide-and-conquer/index.html
+++ b/Algorithm/divide-and-conquer/index.html
@@ -425,9 +425,9 @@ 【分治】随机排列
-
+
- a_template
+ dfs-and-similar
上一篇
@@ -435,8 +435,8 @@ 【分治】随机排列
-
- binary-search
+
+ dp
下一篇
diff --git a/Algorithm/dp/index.html b/Algorithm/dp/index.html
index 545026ecf..7bf9f8993 100644
--- a/Algorithm/dp/index.html
+++ b/Algorithm/dp/index.html
@@ -979,9 +979,9 @@ 【状压dp】Avoid K Palindrome
-
+
- dfs-and-similar
+ divide-and-conquer
上一篇
@@ -989,6 +989,12 @@ 【状压dp】Avoid K Palindrome
+
+ data-structure
+ 下一篇
+
+
+
diff --git a/Algorithm/games/index.html b/Algorithm/games/index.html
index 0bca8277d..6500ef3e3 100644
--- a/Algorithm/games/index.html
+++ b/Algorithm/games/index.html
@@ -426,9 +426,9 @@ 【博弈/贪心/交
-
+
- geometry
+ back-end-guide
上一篇
@@ -436,8 +436,8 @@ 【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+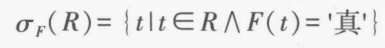
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+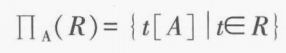
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+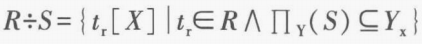
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【dfs】将
-
- dp
+
+ divide-and-conquer
下一篇
diff --git a/Algorithm/divide-and-conquer/index.html b/Algorithm/divide-and-conquer/index.html
index 6cf89a0ae..2f3819536 100644
--- a/Algorithm/divide-and-conquer/index.html
+++ b/Algorithm/divide-and-conquer/index.html
@@ -425,9 +425,9 @@ 【分治】随机排列
-
+
- a_template
+ dfs-and-similar
上一篇
@@ -435,8 +435,8 @@ 【分治】随机排列
-
- binary-search
+
+ dp
下一篇
diff --git a/Algorithm/dp/index.html b/Algorithm/dp/index.html
index 545026ecf..7bf9f8993 100644
--- a/Algorithm/dp/index.html
+++ b/Algorithm/dp/index.html
@@ -979,9 +979,9 @@ 【状压dp】Avoid K Palindrome
-
+
- dfs-and-similar
+ divide-and-conquer
上一篇
@@ -989,6 +989,12 @@ 【状压dp】Avoid K Palindrome
+
+ data-structure
+ 下一篇
+
+
+
diff --git a/Algorithm/games/index.html b/Algorithm/games/index.html
index 0bca8277d..6500ef3e3 100644
--- a/Algorithm/games/index.html
+++ b/Algorithm/games/index.html
@@ -426,9 +426,9 @@ 【博弈/贪心/交
-
+
- geometry
+ back-end-guide
上一篇
@@ -436,8 +436,8 @@ 【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+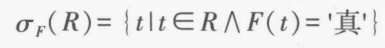
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+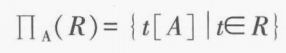
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+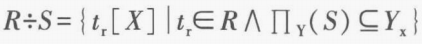
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【分治】随机排列
【分治】随机排列
【状压dp】Avoid K Palindrome
-
+
- dfs-and-similar
+ divide-and-conquer
上一篇
@@ -989,6 +989,12 @@ 【状压dp】Avoid K Palindrome
+
+ data-structure
+ 下一篇
+
+
+
diff --git a/Algorithm/games/index.html b/Algorithm/games/index.html
index 0bca8277d..6500ef3e3 100644
--- a/Algorithm/games/index.html
+++ b/Algorithm/games/index.html
@@ -426,9 +426,9 @@ 【博弈/贪心/交
-
+
- geometry
+ back-end-guide
上一篇
@@ -436,8 +436,8 @@ 【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+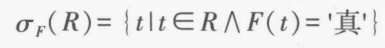
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+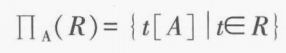
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+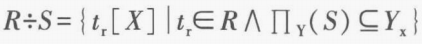
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【状压dp】Avoid K Palindrome
+
+ data-structure
+ 下一篇
+
+
+
diff --git a/Algorithm/games/index.html b/Algorithm/games/index.html
index 0bca8277d..6500ef3e3 100644
--- a/Algorithm/games/index.html
+++ b/Algorithm/games/index.html
@@ -426,9 +426,9 @@ 【博弈/贪心/交
-
+
- geometry
+ back-end-guide
上一篇
@@ -436,8 +436,8 @@ 【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+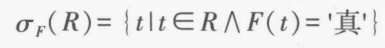
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+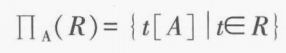
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+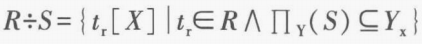
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【博弈/贪心/交
-
- hashing
+
+ graphs
下一篇
diff --git a/Algorithm/geometry/index.html b/Algorithm/geometry/index.html
index c81407478..0d1ee8f7d 100644
--- a/Algorithm/geometry/index.html
+++ b/Algorithm/geometry/index.html
@@ -472,9 +472,9 @@ 【凸包】奶牛过马路
-
+
- back-end-guide
+ number-theory
上一篇
@@ -482,8 +482,8 @@ 【凸包】奶牛过马路
-
- games
+
+ prefix-and-difference
下一篇
diff --git a/Algorithm/graphs/index.html b/Algorithm/graphs/index.html
index d0032bb0b..e74a766ae 100644
--- a/Algorithm/graphs/index.html
+++ b/Algorithm/graphs/index.html
@@ -694,9 +694,9 @@ 【LCA】树的直径
-
+
- number-theory
+ games
上一篇
diff --git a/Algorithm/greedy/index.html b/Algorithm/greedy/index.html
index 8c18674f5..b1c88b80f 100644
--- a/Algorithm/greedy/index.html
+++ b/Algorithm/greedy/index.html
@@ -819,8 +819,8 @@ 【按位贪心/分类讨论】
-
- prefix-and-difference
+
+ hashing
下一篇
diff --git a/Algorithm/hashing/index.html b/Algorithm/hashing/index.html
index d972de37d..fe8fba200 100644
--- a/Algorithm/hashing/index.html
+++ b/Algorithm/hashing/index.html
@@ -466,9 +466,9 @@ 【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+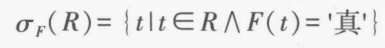
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+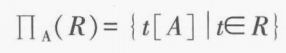
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+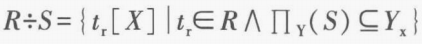
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【凸包】奶牛过马路
【凸包】奶牛过马路
【LCA】树的直径
【按位贪心/分类讨论】
【哈希/枚举/思维】T
-
+
- games
+ greedy
上一篇
diff --git a/Algorithm/number-theory/index.html b/Algorithm/number-theory/index.html
index 1654b35fe..edf6fc8e1 100644
--- a/Algorithm/number-theory/index.html
+++ b/Algorithm/number-theory/index.html
@@ -484,8 +484,8 @@ 【组合数学】序列数量
-
- graphs
+
+ geometry
下一篇
diff --git a/Algorithm/prefix-and-difference/index.html b/Algorithm/prefix-and-difference/index.html
index c19517c84..efba6876c 100644
--- a/Algorithm/prefix-and-difference/index.html
+++ b/Algorithm/prefix-and-difference/index.html
@@ -463,9 +463,9 @@ 【差分/贪心】增减序列
-
+
- greedy
+ geometry
上一篇
diff --git a/BackEnd/back-end-guide/index.html b/BackEnd/back-end-guide/index.html
index 3378a59b0..b82aa224a 100644
--- a/BackEnd/back-end-guide/index.html
+++ b/BackEnd/back-end-guide/index.html
@@ -433,8 +433,8 @@ 参考
-
- geometry
+
+ games
下一篇
diff --git a/DataBase/data-base-guide/index.html b/DataBase/data-base-guide/index.html
index 53a2635bc..871fb5d44 100644
--- a/DataBase/data-base-guide/index.html
+++ b/DataBase/data-base-guide/index.html
@@ -421,9 +421,9 @@ 参考
-
+
- self-config
+ solve-clion-decoding-error
上一篇
diff --git a/DevTools/CLion/solve-clion-decoding-error/index.html b/DevTools/CLion/solve-clion-decoding-error/index.html
index 22a2baff3..25dc62c8e 100644
--- a/DevTools/CLion/solve-clion-decoding-error/index.html
+++ b/DevTools/CLion/solve-clion-decoding-error/index.html
@@ -451,9 +451,9 @@ 解决方案
-
+
- git-self-define-command
+ self-config
上一篇
@@ -461,8 +461,8 @@ 解决方案
-
- self-config
+
+ data-base-guide
下一篇
diff --git a/DevTools/DevCpp/devc-self-config/index.html b/DevTools/DevCpp/devc-self-config/index.html
index 76a8b8c2b..984cd8c16 100644
--- a/DevTools/DevCpp/devc-self-config/index.html
+++ b/DevTools/DevCpp/devc-self-config/index.html
@@ -452,9 +452,9 @@ 四、快捷键选项
-
+
- solve-clion-decoding-error
+ git-self-define-command
上一篇
@@ -462,8 +462,8 @@ 四、快捷键选项
-
- data-base-guide
+
+ solve-clion-decoding-error
下一篇
diff --git a/DevTools/Git/git-self-define-command/index.html b/DevTools/Git/git-self-define-command/index.html
index 4a7f0f94e..64c633173 100644
--- a/DevTools/Git/git-self-define-command/index.html
+++ b/DevTools/Git/git-self-define-command/index.html
@@ -449,8 +449,8 @@ 宏定义
-
- solve-clion-decoding-error
+
+ self-config
下一篇
diff --git a/GPA/2nd-term/ObjectOrientedClassDesign/index.html b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
index 9d92f3b61..3fcf60c27 100644
--- a/GPA/2nd-term/ObjectOrientedClassDesign/index.html
+++ b/GPA/2nd-term/ObjectOrientedClassDesign/index.html
@@ -437,9 +437,9 @@ 代码仓库
-
+
- LinearAlgebra
+ DataStructureClassDesign
上一篇
diff --git a/GPA/3rd-term/DataStructure/index.html b/GPA/3rd-term/DataStructure/index.html
index 4c42f85d6..04ca78c9c 100644
--- a/GPA/3rd-term/DataStructure/index.html
+++ b/GPA/3rd-term/DataStructure/index.html
@@ -1415,8 +1415,8 @@ 10.8 归并排序
-
- DataStructureClassDesign
+
+ LinearAlgebra
下一篇
diff --git a/GPA/3rd-term/DataStructureClassDesign/index.html b/GPA/3rd-term/DataStructureClassDesign/index.html
index 4eda3d393..54fb1b882 100644
--- a/GPA/3rd-term/DataStructureClassDesign/index.html
+++ b/GPA/3rd-term/DataStructureClassDesign/index.html
@@ -601,9 +601,9 @@ 仓库地址
-
+
- DataStructure
+ DigitalLogicCircuit
上一篇
@@ -611,8 +611,8 @@ 仓库地址
-
- DigitalLogicCircuit
+
+ ObjectOrientedClassDesign
下一篇
diff --git a/GPA/3rd-term/DigitalLogicCircuit/index.html b/GPA/3rd-term/DigitalLogicCircuit/index.html
index 4ee9c207a..e617578c3 100644
--- a/GPA/3rd-term/DigitalLogicCircuit/index.html
+++ b/GPA/3rd-term/DigitalLogicCircuit/index.html
@@ -1522,9 +1522,9 @@ 6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+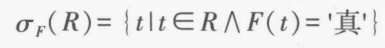
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+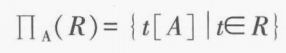
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+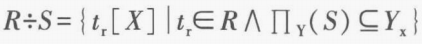
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
【组合数学】序列数量
【差分/贪心】增减序列
参考
参考
解决方案
解决方案
四、快捷键选项
四、快捷键选项
宏定义
代码仓库
10.8 归并排序
仓库地址
仓库地址
6.3 用 verilog 描述
-
+
- DataStructureClassDesign
+ LinearAlgebra
上一篇
@@ -1532,8 +1532,8 @@ 6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+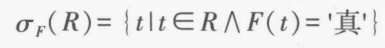
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+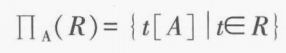
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+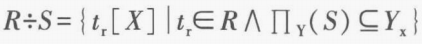
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
6.3 用 verilog 描述
-
- LinearAlgebra
+
+ DataStructureClassDesign
下一篇
diff --git a/GPA/3rd-term/LinearAlgebra/index.html b/GPA/3rd-term/LinearAlgebra/index.html
index 183275f32..87825a223 100644
--- a/GPA/3rd-term/LinearAlgebra/index.html
+++ b/GPA/3rd-term/LinearAlgebra/index.html
@@ -1177,9 +1177,9 @@ 行列式角度
-
+
- DigitalLogicCircuit
+ DataStructure
上一篇
@@ -1187,8 +1187,8 @@ 行列式角度
-
- ObjectOrientedClassDesign
+
+ DigitalLogicCircuit
下一篇
diff --git a/GPA/4th-term/MachineLearning/index.html b/GPA/4th-term/MachineLearning/index.html
index 364e88929..e98f2562f 100644
--- a/GPA/4th-term/MachineLearning/index.html
+++ b/GPA/4th-term/MachineLearning/index.html
@@ -104,7 +104,7 @@
-
+
@@ -398,7 +398,7 @@ MachineLearning
- 本文最后更新于 2024年8月28日 中午
+ 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@ 5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
@@ -1938,7 +1938,7 @@ 考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html
index 952d5ddf6..9c6404da2 100644
--- a/GPA/4th-term/OptMethod/index.html
+++ b/GPA/4th-term/OptMethod/index.html
@@ -1853,8 +1853,8 @@ 四、计算 68'
-
- PyAlgo
+
+ ProbAndStat
下一篇
diff --git a/GPA/4th-term/ProbAndStat/index.html b/GPA/4th-term/ProbAndStat/index.html
index cb533102c..21335493c 100644
--- a/GPA/4th-term/ProbAndStat/index.html
+++ b/GPA/4th-term/ProbAndStat/index.html
@@ -1932,9 +1932,9 @@ 8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
-SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并 ∩ \cap − - ∪ \cup × \times
+专门的关系运算
+先补充几个必要的符号表示:
+
+- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+- 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
+- 串接。将两个元组左右连接。
+- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
+选择 σ F ( R ) \sigma_F(R) F (Filter) F\text{(Filter)} F F ( ) > θ > ¬ > ∧ > ∨ ()>\theta>\lnot>\land>\lor θ = { > , < , ≥ , ≤ , = , ≠ } \theta=\{ >,<,\ge,\le,=,\ne \}
+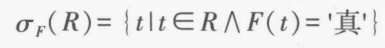
+投影 Π A ( R ) \Pi_A(R) A (Attribute) A\text{(Attribute)}
+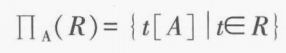
+连接 R ⋈ S R \Join S R × S R\times S θ \theta
+
+
+- 一般连接。就是上述所述。
+- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
+- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
+
+除法 R ÷ S R \div S R ( X , Y ) R(X,Y) S ( Y , Z ) S(Y,Z) R ( X ) R(X) S ( X ) S(X)
+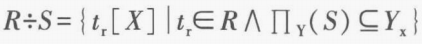
+3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@ 并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
index db9812c51..7999c5a76 100644
--- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
+++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html
@@ -28,7 +28,7 @@
-
+
@@ -247,7 +247,7 @@
@@ -322,7 +322,7 @@ NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨
+ 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@ 线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+
+- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
+- Relu 函数
+
+1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@ 个人大作业
diff --git a/README/index.html b/README/index.html
index 4ca6497e4..93afa74f4 100644
--- a/README/index.html
+++ b/README/index.html
@@ -450,8 +450,8 @@ 未来展望
-
- a_template
+
+ binary-search
下一篇
diff --git a/archives/2024/03/index.html b/archives/2024/03/index.html
index 8b8970ce3..0f97c6525 100644
--- a/archives/2024/03/index.html
+++ b/archives/2024/03/index.html
@@ -302,9 +302,9 @@
-
+
- PyAlgo
+ ProbAndStat
diff --git a/archives/2024/03/page/2/index.html b/archives/2024/03/page/2/index.html
index f24dff2be..faae61dc7 100644
--- a/archives/2024/03/page/2/index.html
+++ b/archives/2024/03/page/2/index.html
@@ -248,9 +248,9 @@
2024
-
+
- ProbAndStat
+ PyAlgo
@@ -272,9 +272,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -284,9 +284,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/03/page/3/index.html b/archives/2024/03/page/3/index.html
index aefa72d85..09f5763a4 100644
--- a/archives/2024/03/page/3/index.html
+++ b/archives/2024/03/page/3/index.html
@@ -272,15 +272,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/archives/2024/03/page/4/index.html b/archives/2024/03/page/4/index.html
index db69a353f..f99a4bdb0 100644
--- a/archives/2024/03/page/4/index.html
+++ b/archives/2024/03/page/4/index.html
@@ -248,39 +248,39 @@
2024
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/archives/2024/03/page/5/index.html b/archives/2024/03/page/5/index.html
index 5054a0334..3f0fcd50b 100644
--- a/archives/2024/03/page/5/index.html
+++ b/archives/2024/03/page/5/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/2024/page/5/index.html b/archives/2024/page/5/index.html
index 120457577..66a4d1f1c 100644
--- a/archives/2024/page/5/index.html
+++ b/archives/2024/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/2024/page/6/index.html b/archives/2024/page/6/index.html
index 5c604e32c..3aa18e6d7 100644
--- a/archives/2024/page/6/index.html
+++ b/archives/2024/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/2024/page/7/index.html b/archives/2024/page/7/index.html
index 782d1fabf..8243ca392 100644
--- a/archives/2024/page/7/index.html
+++ b/archives/2024/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/2024/page/8/index.html b/archives/2024/page/8/index.html
index 47adf790b..4ba332173 100644
--- a/archives/2024/page/8/index.html
+++ b/archives/2024/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/2024/page/9/index.html b/archives/2024/page/9/index.html
index 8790cc335..842356af0 100644
--- a/archives/2024/page/9/index.html
+++ b/archives/2024/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/archives/page/5/index.html b/archives/page/5/index.html
index 5ca7a5456..a6acfe70a 100644
--- a/archives/page/5/index.html
+++ b/archives/page/5/index.html
@@ -290,15 +290,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/archives/page/6/index.html b/archives/page/6/index.html
index e3de1101d..6ed0c14a7 100644
--- a/archives/page/6/index.html
+++ b/archives/page/6/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/archives/page/7/index.html b/archives/page/7/index.html
index 2366ae904..88ef0b241 100644
--- a/archives/page/7/index.html
+++ b/archives/page/7/index.html
@@ -260,15 +260,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
@@ -296,15 +296,15 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
diff --git a/archives/page/8/index.html b/archives/page/8/index.html
index b189179b5..e73aa01c9 100644
--- a/archives/page/8/index.html
+++ b/archives/page/8/index.html
@@ -248,27 +248,27 @@
2024
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -284,27 +284,27 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
diff --git a/archives/page/9/index.html b/archives/page/9/index.html
index 184d679f7..c916f215d 100644
--- a/archives/page/9/index.html
+++ b/archives/page/9/index.html
@@ -248,15 +248,15 @@
2024
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/Algorithm/index.html b/categories/Algorithm/index.html
index c61a11d4a..85ac49c79 100644
--- a/categories/Algorithm/index.html
+++ b/categories/Algorithm/index.html
@@ -254,39 +254,39 @@
-
+
- geometry
+ games
-
+
- games
+ graphs
-
+
- hashing
+ greedy
-
+
- number-theory
+ hashing
-
+
- graphs
+ number-theory
-
+
- greedy
+ geometry
@@ -296,15 +296,15 @@
-
+
- a_template
+ binary-search
-
+
- divide-and-conquer
+ a_template
diff --git a/categories/Algorithm/page/2/index.html b/categories/Algorithm/page/2/index.html
index 9d33edc2d..826aca71f 100644
--- a/categories/Algorithm/page/2/index.html
+++ b/categories/Algorithm/page/2/index.html
@@ -248,27 +248,27 @@
2024
-
+
- binary-search
+ dfs-and-similar
-
+
- data-structure
+ divide-and-conquer
-
+
- dfs-and-similar
+ dp
-
+
- dp
+ data-structure
diff --git a/categories/DevTools/index.html b/categories/DevTools/index.html
index e6644197a..5228e0f5f 100644
--- a/categories/DevTools/index.html
+++ b/categories/DevTools/index.html
@@ -290,15 +290,15 @@
-
+
- solve-clion-decoding-error
+ self-config
-
+
- self-config
+ solve-clion-decoding-error
diff --git a/categories/GPA/3rd-term/index.html b/categories/GPA/3rd-term/index.html
index 0a36936e2..de3d5d6ee 100644
--- a/categories/GPA/3rd-term/index.html
+++ b/categories/GPA/3rd-term/index.html
@@ -260,9 +260,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -272,9 +272,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/categories/GPA/4th-term/index.html b/categories/GPA/4th-term/index.html
index 2a964b74f..f47c5e107 100644
--- a/categories/GPA/4th-term/index.html
+++ b/categories/GPA/4th-term/index.html
@@ -272,15 +272,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
diff --git a/categories/GPA/page/2/index.html b/categories/GPA/page/2/index.html
index 1c3003054..2bd298fae 100644
--- a/categories/GPA/page/2/index.html
+++ b/categories/GPA/page/2/index.html
@@ -260,15 +260,15 @@
-
+
- PyAlgo
+ ProbAndStat
-
+
- ProbAndStat
+ PyAlgo
@@ -290,9 +290,9 @@
-
+
- DataStructureClassDesign
+ LinearAlgebra
@@ -302,9 +302,9 @@
-
+
- LinearAlgebra
+ DataStructureClassDesign
diff --git a/local-search.xml b/local-search.xml
index 38bf1abba..ab512c20a 100644
--- a/local-search.xml
+++ b/local-search.xml
@@ -514,7 +514,7 @@
/GPA/5th-term/NeuralNetworkAndDeepLearning/
- 神经网络与深度学习
行列式角度
行列式角度
MachineLearning
- 本文最后更新于 2024年8月28日 中午 + 本文最后更新于 2024年10月10日 下午
@@ -1300,11 +1300,11 @@5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权 以及所有功能神经元中的阈值 ,我们需要通过每一次迭代的结果进行参数的修正,对于连接权 而言,我们假设当前感知机的输出为 ,则连接权 应做以下调整。其中 为学习率。
-
考试大纲
diff --git a/GPA/4th-term/OptMethod/index.html b/GPA/4th-term/OptMethod/index.html index 952d5ddf6..9c6404da2 100644 --- a/GPA/4th-term/OptMethod/index.html +++ b/GPA/4th-term/OptMethod/index.html @@ -1853,8 +1853,8 @@四、计算 68'
8.3 单个正态总体方
-
+
- PyAlgo
+ OptMethod
上一篇
@@ -1942,8 +1942,8 @@ 8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
8.3 单个正态总体方
-
- SysBasic
+
+ PyAlgo
下一篇
diff --git a/GPA/4th-term/PyAlgo/index.html b/GPA/4th-term/PyAlgo/index.html
index d0a762b0b..e7f3b0d72 100644
--- a/GPA/4th-term/PyAlgo/index.html
+++ b/GPA/4th-term/PyAlgo/index.html
@@ -504,9 +504,9 @@ 考后碎碎念
-
+
- OptMethod
+ ProbAndStat
上一篇
@@ -514,8 +514,8 @@ 考后碎碎念
-
- ProbAndStat
+
+ SysBasic
下一篇
diff --git a/GPA/4th-term/SysBasic/index.html b/GPA/4th-term/SysBasic/index.html
index 3108c248b..4b2bbd30c 100644
--- a/GPA/4th-term/SysBasic/index.html
+++ b/GPA/4th-term/SysBasic/index.html
@@ -1272,9 +1272,9 @@ 4.4.2 重定位过程
-
+
- ProbAndStat
+ PyAlgo
上一篇
diff --git a/GPA/5th-term/DataBase/index.html b/GPA/5th-term/DataBase/index.html
index 138b1568f..d070e6d5f 100644
--- a/GPA/5th-term/DataBase/index.html
+++ b/GPA/5th-term/DataBase/index.html
@@ -27,8 +27,12 @@
+
+
+
+
-
+
@@ -247,7 +251,7 @@
@@ -258,7 +262,7 @@
- 13 分钟
+ 16 分钟
@@ -322,7 +326,7 @@ DataBase
- 本文最后更新于 2024年9月26日 晚上
+ 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@ 前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统 → \to → \to
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
考后碎碎念
考后碎碎念
4.4.2 重定位过程
DataBase
- 本文最后更新于 2024年9月26日 晚上 + 本文最后更新于 2024年10月10日 上午
@@ -402,7 +406,7 @@前言
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
-绪论
+1 绪论
数据库发展范式:人工系统
数据库系统概念图:
---
@@ -441,10 +445,13 @@ 绪论
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
-关系模型
-基本概念:
+2 关系模型
+2.1 基本概念
+基本概念:R = ( A 1 : D 1 , A 2 : D 2 , . . . , A n : D n , ) R = (A_1:D_1,A_2:D_2,...,A_n:D_n,)

+2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
+2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
-
@@ -476,9 +483,34 @@
关系模型
SQL
-安全性
-完整性
+2.4 关系代数
+用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
+传统的集合运算
+并
专门的关系运算
+先补充几个必要的符号表示:
+-
+
- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i
+ - 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。 +
- 串接。将两个元组左右连接。 +
- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
+
选择
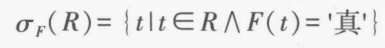
投影
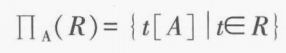
连接

-
+
- 一般连接。就是上述所述。 +
- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。 +
- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。 +
除法
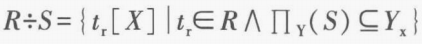
3 SQL
+4 安全性
+5 完整性
开发篇
关系数据理论
数据库设计
@@ -554,7 +586,7 @@并发
diff --git a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html index db9812c51..7999c5a76 100644 --- a/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html +++ b/GPA/5th-term/NeuralNetworkAndDeepLearning/index.html @@ -28,7 +28,7 @@ - + @@ -247,7 +247,7 @@ @@ -322,7 +322,7 @@NeuralNetworkAndDeepLearning
- 本文最后更新于 2024年10月8日 凌晨 + 本文最后更新于 2024年10月10日 下午
@@ -420,10 +420,15 @@线性模型
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
-基础神经网络模型
-前馈神经网络
-卷积神经网络
-循环神经网络
+1 基础神经网络模型
+1.1 前馈神经网络
+神经元中的激活函数:
+-
+
- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。 +
- Relu 函数 +
1.2 卷积神经网络
+1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
@@ -502,7 +507,7 @@个人大作业
diff --git a/README/index.html b/README/index.html index 4ca6497e4..93afa74f4 100644 --- a/README/index.html +++ b/README/index.html @@ -450,8 +450,8 @@未来展望
2024
- + -2024
- + -2024
- + -2024
- + -2024
- + -2024
- + -2024
- + -2024
- + -前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 宋歌 | 3 | 自发课 |
成绩组成:
| 小组作业 | 个人大作业 |
|---|---|
| 40% | 60% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 神经网络与深度学习 | 《神经网络与深度学习》 | 1 | 邱锡鹏 | 机械工业出版社 | 978-7-111-64968-7 |
学习资源:
为什么要学这门课?
还记得 NJU 的 jyy 老师在上 OS 时说过的一句话,“我们现在学习的微积分是 300 年前的人类智慧结晶,何不再学学 50 年前的人类智慧结晶呢?”印象深刻。当一切都可以用层层嵌套的简单函数模拟时,人类社会必将发生翻天覆地的变化!
会收获什么?
如何学习特征?如何优化调参?为什么要这样做?背后的原理是什么?
概述
绪论
表示学习是什么?与传统的特征工程目的一致,为了得到数据中的更好的特征。不同的是,特征工程中的策略都是可控的方式,而表示学习就是利用深度学习从数据中学习高层的有效特征。
深度学习是什么?我们知道机器学习就是在手动处理完特征后,构建对应的模型 预测输出。而深度学习就是将机器学习的手动特征工程也用模型进行 表示学习 来学习出有效特征,然后继续构建模型 预测输出。如下图所示:

为什么会有深度学习?最简单的一点就是,很多特征我们根本没法定义一种表示规则来表示特征,比如说对于图像,怎么定义复杂的图像的特征呢?比如说对于音频,又怎么定义复杂的音频的特征呢?没办法,我们直接学特征!
神经网络是什么?就是万千模型中的一种,仅此而已。
为什么用神经网络进行深度学习?有了上面对深度学习定义的理解,可以发现其中最具有挑战性的特点就是,模型怎么知道什么才是好特征?什么是不好的特征?神经网络可以很好的解决这个问题。通过由浅到深层层神经元的特征提取,越深的神经元就可以学习更高语义的特征。说的高大上一点就是,神经网络可以很好的解决深度学习中的「贡献度分配」问题。
机器学习概述
数据
线性模型
学习任务:分类、回归。
学习准则:
- 经验风险最小化:通过 最小化训练集上的损失函数 来学习模型参数。例如:线性回归中的最小二乘损失。
- 结构风险最小化:引入 正则化 来控制模型的复杂度,避免过拟合。
- 最大似然估计:通过 最大化模型在给定数据上的似然函数 来估计模型参数。例如二分类 logistic 和多分类 softmax 中的交叉熵损失。
- 最大后验估计:结合了似然函数和 先验 分布,在贝叶斯框架下估计模型参数。
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
基础神经网络模型
前馈神经网络
卷积神经网络
循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
概率图模型
深度生成模型
强化学习
深度强化学习
个人大作业
- 背景介绍:做好国内外研究现状的调研。
- 项目理解:深入对模型与代码的理解。
- 充分实验:对比实验、验证实验(消融实验)、参数实验(验证模型对不同的参数的敏感性)。
- 项目总结。
前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 宋歌 | 3 | 自发课 |
成绩组成:
| 小组作业 | 个人大作业 |
|---|---|
| 40% | 60% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 神经网络与深度学习 | 《神经网络与深度学习》 | 1 | 邱锡鹏 | 机械工业出版社 | 978-7-111-64968-7 |
学习资源:
为什么要学这门课?
还记得 NJU 的 jyy 老师在上 OS 时说过的一句话,“我们现在学习的微积分是 300 年前的人类智慧结晶,何不再学学 50 年前的人类智慧结晶呢?”印象深刻。当一切都可以用层层嵌套的简单函数模拟时,人类社会必将发生翻天覆地的变化!
会收获什么?
如何学习特征?如何优化调参?为什么要这样做?背后的原理是什么?
概述
绪论
表示学习是什么?与传统的特征工程目的一致,为了得到数据中的更好的特征。不同的是,特征工程中的策略都是可控的方式,而表示学习就是利用深度学习从数据中学习高层的有效特征。
深度学习是什么?我们知道机器学习就是在手动处理完特征后,构建对应的模型 预测输出。而深度学习就是将机器学习的手动特征工程也用模型进行 表示学习 来学习出有效特征,然后继续构建模型 预测输出。如下图所示:

为什么会有深度学习?最简单的一点就是,很多特征我们根本没法定义一种表示规则来表示特征,比如说对于图像,怎么定义复杂的图像的特征呢?比如说对于音频,又怎么定义复杂的音频的特征呢?没办法,我们直接学特征!
神经网络是什么?就是万千模型中的一种,仅此而已。
为什么用神经网络进行深度学习?有了上面对深度学习定义的理解,可以发现其中最具有挑战性的特点就是,模型怎么知道什么才是好特征?什么是不好的特征?神经网络可以很好的解决这个问题。通过由浅到深层层神经元的特征提取,越深的神经元就可以学习更高语义的特征。说的高大上一点就是,神经网络可以很好的解决深度学习中的「贡献度分配」问题。
机器学习概述
数据
线性模型
学习任务:分类、回归。
学习准则:
- 经验风险最小化:通过 最小化训练集上的损失函数 来学习模型参数。例如:线性回归中的最小二乘损失。
- 结构风险最小化:引入 正则化 来控制模型的复杂度,避免过拟合。
- 最大似然估计:通过 最大化模型在给定数据上的似然函数 来估计模型参数。例如二分类 logistic 和多分类 softmax 中的交叉熵损失。
- 最大后验估计:结合了似然函数和 先验 分布,在贝叶斯框架下估计模型参数。
优化算法:最小二乘法、梯度下降法、拟牛顿法。
有监督学习
1 基础神经网络模型
1.1 前馈神经网络
神经元中的激活函数:
- Sigmoid 函数:例如 logistic 函数和 Tanh 函数。
- Relu 函数
1.2 卷积神经网络
1.3 循环神经网络
记忆与注意力机制
网络优化与正则化
无监督学习
概率图模型
深度生成模型
强化学习
深度强化学习
个人大作业
- 背景介绍:做好国内外研究现状的调研。
- 项目理解:深入对模型与代码的理解。
- 充分实验:对比实验、验证实验(消融实验)、参数实验(验证模型对不同的参数的敏感性)。
- 项目总结。
前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 孔力 | 3.5 | 自发课 |
成绩组成:
| 平时 | 作业+实验 | 期末(闭卷 or 开卷) |
|---|---|---|
| 10% | 40% | 50% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 数据库原理与应用 | 《数据库系统概论》 | 6 | 王珊等 | 高等教育出版社 | 978-7-04-059125-5 |
学习资源:
- 课程官网:数据库系统概论 (ruc.edu.cn)
为什么要学这门课?
感觉没什么意义,毕竟只讲关系型数据库,而这个是再简单不过的数据模型了,哪怕加上了外键也不会很复杂。但我深知 db 的奥妙与深度绝不止于此,但是就目前上课情况来看应该是达不到这种程度了,毕竟连最基本的数据库编程都是不做要求的。
会收获什么?
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
绪论
数据库发展范式:人工系统
数据库系统概念图:
---title: 数据库系统---graph TB DBM[数据库管理员] subgraph 数据 DB[(数据库\n「内模式」)] DBMS[数据库管理系统\n「逻辑模式」] subgraph DBAP[应用程序] direction LR out_model1[「外模式1」] out_model2[「外模式2」] out_model1 <-.-> 应用A out_model1 <-.-> 应用B out_model2 <-.-> 应用C end end DBM --> 数据 DB <-.-> DBMS DBMS <-.-> DBAP数据库的三级模式:从硬件到应用将一个数据库抽象为三层。其中:
- 内模式:硬件存储数据的方式;
- 逻辑模式:数据库管理的方式,也就是数据存储方式的 逻辑 抽象。进而引出后续如何存储数据的「数据模型」概念;
- 外模式:不同的应用对全体数据有不同的访存权限。一个外模式可以对应多个应用程序,但是一个应用程序只能对应一个外模式。
数据模型:逻辑模式的具体实现策略。我们需要对现实世界的数据进行抽象进而便于虚拟化存储,以及后续对数据库进行增删改查等操作。从发展角度来看,数据模型一共经历了三个阶段,分别为 层次模型
三要素:数据结构(二维表)、数据操作(增删改查)和关系的完整性约束(每一个实体能通过主键唯一检索、外键引用必须存在、关系要根据业务需求设定完备)
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
关系模型
基本概念:

关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
关于一对多。例如,一个客户可以购买很多商品,而一个被购买的商品只能隶属于一个客户;
▶实例假设有两个表:
customers和orders。customers表保存客户的信息,orders表保存订单信息。每个订单都应该对应一个客户,所以可以使用外键将这两个表关联起来。创建表
1
2
3
4
5
6
7
8
9
10
11
12
13-- 创建 customers 表
CREATE TABLE customers (
customer_id INT PRIMARY KEY,
customer_name VARCHAR(100)
);
-- 创建 orders 表,order_id 是主键,customer_id 是外键,引用 customers 表中的 customer_id
CREATE TABLE orders (
order_id INT PRIMARY KEY,
order_date DATE,
customer_id INT,
FOREIGN KEY (customer_id) REFERENCES customers(customer_id)
);在上述示例中,
orders表中的customer_id是一个外键,它引用了customers表中的customer_id列。这样一来,只有在customers表中存在的customer_id才能在orders表中作为合法的customer_id。这确保了每个订单都有有效的客户。插入数据(增):当向
orders表中插入一条新记录时,数据库会检查customer_id是否在customers表中存在。如果不存在,插入操作会失败。1
2
3
4
5
6
7
8-- 插入一条合法记录
INSERT INTO customers (customer_id, customer_name) VALUES (1, 'Alice');
-- 插入订单记录,外键 customer_id 存在于 customers 表中
INSERT INTO orders (order_id, order_date, customer_id) VALUES (101, '2024-09-26', 1);
-- 尝试插入一个无效的订单记录(客户ID为2在 customers 表中不存在)
INSERT INTO orders (order_id, order_date, customer_id) VALUES (102, '2024-09-26', 2); -- 会失败删除或更新时(删 | 改):如果试图删除
customers表中的某个customer_id,而该 ID 在orders表中被引用,会引发外键约束错误。可以通过设置外键的级联操作(如ON DELETE CASCADE或ON UPDATE CASCADE)来控制这种行为,使删除或更新操作可以自动级联到相关表。1
2
3
4
5
6
7
8
9
10-- 定义外键时使用级联删除
CREATE TABLE orders (
order_id INT PRIMARY KEY,
order_date DATE,
customer_id INT,
FOREIGN KEY (customer_id) REFERENCES customers(customer_id) ON DELETE CASCADE
);
-- 删除客户1时,orders 表中所有引用 customer_id = 1 的订单都会自动被删除
DELETE FROM customers WHERE customer_id = 1;关于多对多。例如,一门课程需要多门先修课,而一门课程也可以成为很多课程的选修课。
▶实例这里课程与先修课之间的实体对象是相同的,并且一门课程可以有许多门先修课,而一门课程也可能成为很多课程的先修课,如果还是像一对多那样进行存储,即课程表中增加一列先修课,就会导致先修课列中可能出现多个信息的情况,这也就不符合关系型数据库中的第一范式:原子性。因此我们不得不创建一个新表,也就是中间表,来存储课程和先修课之间的关系。
创建表
1
2
3
4
5
6
7
8
9
10
11
12
13
14-- 创建 courses 表
CREATE TABLE courses (
course_id INT PRIMARY KEY,
course_name VARCHAR(100)
);
-- 创建 prerequisites 表,其中 course_id 和 prerequisite_id 都是外键
CREATE TABLE prerequisites (
course_id INT, -- 课程ID
prerequisite_id INT, -- 先修课ID
PRIMARY KEY (course_id, prerequisite_id), -- 组合主键
FOREIGN KEY (course_id) REFERENCES courses(course_id) ON DELETE CASCADE, -- 课程ID外键
FOREIGN KEY (prerequisite_id) REFERENCES courses(course_id) ON DELETE CASCADE -- 先修课ID外键
);在这个设计中:
courses表保存所有课程的基本信息,每门课程都有唯一的course_id。prerequisites表用于表示多对多的先修课关系,其中course_id是当前课程的 ID,prerequisite_id是该课程的先修课程的 ID。两者都引用了courses表中的course_id列,构成多对多的关系。
插入数据(增)
插入课程记录:
1
2
3
4
5-- 插入一些课程记录
INSERT INTO courses (course_id, course_name) VALUES (1, 'Mathematics');
INSERT INTO courses (course_id, course_name) VALUES (2, 'Physics');
INSERT INTO courses (course_id, course_name) VALUES (3, 'Computer Science');
INSERT INTO courses (course_id, course_name) VALUES (4, 'Linear Algebra');插入先修课关系记录:
1
2
3
4
5
6-- 课程 Computer Science 需要 Mathematics 和 Physics 作为先修课
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (3, 1); -- Computer Science -> Mathematics
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (3, 2); -- Computer Science -> Physics
-- 课程 Physics 需要 Linear Algebra 作为先修课
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (2, 4); -- Physics -> Linear Algebra在上述例子中:
prerequisites表表示课程之间的先修关系。例如,Computer Science课程的course_id是 3,它的先修课是Mathematics(prerequisite_id为 1)和Physics(prerequisite_id为 2)。- 通过这种方式,可以表示一门课程有多门先修课,同时一门课程也可以作为多门课程的先修课。
- 插入的
course_id和prerequisite_id必须都是courses表中已有的课程,否则会插入失败。
删除数据(删)
由于在创建表时设置了级联操作
ON DELETE CASCADE,因此当我们删除任何一个存在的课程时,与该课程相关的所有先修课信息也都会被级联删除。无论该课程是其他课程的先修课,还是它自身有先修课。
SQL
安全性
完整性
开发篇
关系数据理论
数据库设计
数据库编程 *
这一章不作考试要求。樂。
进阶篇
关系数据库存储管理
关系查询
怎么查询关系的?又可以怎么优化查询策略呢?
数据库恢复技术
并发
]]>前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 孔力 | 3.5 | 自发课 |
成绩组成:
| 平时 | 作业+实验 | 期末(闭卷 or 开卷) |
|---|---|---|
| 10% | 40% | 50% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 数据库原理与应用 | 《数据库系统概论》 | 6 | 王珊等 | 高等教育出版社 | 978-7-04-059125-5 |
学习资源:
- 课程官网:数据库系统概论 (ruc.edu.cn)
为什么要学这门课?
感觉没什么意义,毕竟只讲关系型数据库,而这个是再简单不过的数据模型了,哪怕加上了外键也不会很复杂。但我深知 db 的奥妙与深度绝不止于此,但是就目前上课情况来看应该是达不到这种程度了,毕竟连最基本的数据库编程都是不做要求的。
会收获什么?
熟悉一下关系型数据库的理论吧,顺便准备好被国产的 openGuass ex 一把。其余的数据库类型以及拓展知识就靠自学吧。
基础篇
1 绪论
数据库发展范式:人工系统
数据库系统概念图:
---title: 数据库系统---graph TB DBM[数据库管理员] subgraph 数据 DB[(数据库\n「内模式」)] DBMS[数据库管理系统\n「逻辑模式」] subgraph DBAP[应用程序] direction LR out_model1[「外模式1」] out_model2[「外模式2」] out_model1 <-.-> 应用A out_model1 <-.-> 应用B out_model2 <-.-> 应用C end end DBM --> 数据 DB <-.-> DBMS DBMS <-.-> DBAP数据库的三级模式:从硬件到应用将一个数据库抽象为三层。其中:
- 内模式:硬件存储数据的方式;
- 逻辑模式:数据库管理的方式,也就是数据存储方式的 逻辑 抽象。进而引出后续如何存储数据的「数据模型」概念;
- 外模式:不同的应用对全体数据有不同的访存权限。一个外模式可以对应多个应用程序,但是一个应用程序只能对应一个外模式。
数据模型:逻辑模式的具体实现策略。我们需要对现实世界的数据进行抽象进而便于虚拟化存储,以及后续对数据库进行增删改查等操作。从发展角度来看,数据模型一共经历了三个阶段,分别为 层次模型
三要素:数据结构(二维表)、数据操作(增删改查)和关系的完整性约束(每一个实体能通过主键唯一检索、外键引用必须存在、关系要根据业务需求设定完备)
名词对照:关系(一张表)、元组(一行数据)、属性(一个字段)和码(主键)。
2 关系模型
2.1 基本概念
基本概念:

2.2 关系操作
关系操作的最小单位是什么?所有的增删改查都是以集合为最小单位。
2.3 关系的完整性
外键是什么?有什么用?一张表的外键必须是另一张表的主键以确保数据的完整性,因为主键是必须全部存在的。当然,外键也可以引用本表的主键。有了外键就可以实现表与表之间一对多或多对多的关系。
关于一对多。例如,一个客户可以购买很多商品,而一个被购买的商品只能隶属于一个客户;
▶实例假设有两个表:
customers和orders。customers表保存客户的信息,orders表保存订单信息。每个订单都应该对应一个客户,所以可以使用外键将这两个表关联起来。创建表
1
2
3
4
5
6
7
8
9
10
11
12
13-- 创建 customers 表
CREATE TABLE customers (
customer_id INT PRIMARY KEY,
customer_name VARCHAR(100)
);
-- 创建 orders 表,order_id 是主键,customer_id 是外键,引用 customers 表中的 customer_id
CREATE TABLE orders (
order_id INT PRIMARY KEY,
order_date DATE,
customer_id INT,
FOREIGN KEY (customer_id) REFERENCES customers(customer_id)
);在上述示例中,
orders表中的customer_id是一个外键,它引用了customers表中的customer_id列。这样一来,只有在customers表中存在的customer_id才能在orders表中作为合法的customer_id。这确保了每个订单都有有效的客户。插入数据(增):当向
orders表中插入一条新记录时,数据库会检查customer_id是否在customers表中存在。如果不存在,插入操作会失败。1
2
3
4
5
6
7
8-- 插入一条合法记录
INSERT INTO customers (customer_id, customer_name) VALUES (1, 'Alice');
-- 插入订单记录,外键 customer_id 存在于 customers 表中
INSERT INTO orders (order_id, order_date, customer_id) VALUES (101, '2024-09-26', 1);
-- 尝试插入一个无效的订单记录(客户ID为2在 customers 表中不存在)
INSERT INTO orders (order_id, order_date, customer_id) VALUES (102, '2024-09-26', 2); -- 会失败删除或更新时(删 | 改):如果试图删除
customers表中的某个customer_id,而该 ID 在orders表中被引用,会引发外键约束错误。可以通过设置外键的级联操作(如ON DELETE CASCADE或ON UPDATE CASCADE)来控制这种行为,使删除或更新操作可以自动级联到相关表。1
2
3
4
5
6
7
8
9
10-- 定义外键时使用级联删除
CREATE TABLE orders (
order_id INT PRIMARY KEY,
order_date DATE,
customer_id INT,
FOREIGN KEY (customer_id) REFERENCES customers(customer_id) ON DELETE CASCADE
);
-- 删除客户1时,orders 表中所有引用 customer_id = 1 的订单都会自动被删除
DELETE FROM customers WHERE customer_id = 1;关于多对多。例如,一门课程需要多门先修课,而一门课程也可以成为很多课程的选修课。
▶实例这里课程与先修课之间的实体对象是相同的,并且一门课程可以有许多门先修课,而一门课程也可能成为很多课程的先修课,如果还是像一对多那样进行存储,即课程表中增加一列先修课,就会导致先修课列中可能出现多个信息的情况,这也就不符合关系型数据库中的第一范式:原子性。因此我们不得不创建一个新表,也就是中间表,来存储课程和先修课之间的关系。
创建表
1
2
3
4
5
6
7
8
9
10
11
12
13
14-- 创建 courses 表
CREATE TABLE courses (
course_id INT PRIMARY KEY,
course_name VARCHAR(100)
);
-- 创建 prerequisites 表,其中 course_id 和 prerequisite_id 都是外键
CREATE TABLE prerequisites (
course_id INT, -- 课程ID
prerequisite_id INT, -- 先修课ID
PRIMARY KEY (course_id, prerequisite_id), -- 组合主键
FOREIGN KEY (course_id) REFERENCES courses(course_id) ON DELETE CASCADE, -- 课程ID外键
FOREIGN KEY (prerequisite_id) REFERENCES courses(course_id) ON DELETE CASCADE -- 先修课ID外键
);在这个设计中:
courses表保存所有课程的基本信息,每门课程都有唯一的course_id。prerequisites表用于表示多对多的先修课关系,其中course_id是当前课程的 ID,prerequisite_id是该课程的先修课程的 ID。两者都引用了courses表中的course_id列,构成多对多的关系。
插入数据(增)
插入课程记录:
1
2
3
4
5-- 插入一些课程记录
INSERT INTO courses (course_id, course_name) VALUES (1, 'Mathematics');
INSERT INTO courses (course_id, course_name) VALUES (2, 'Physics');
INSERT INTO courses (course_id, course_name) VALUES (3, 'Computer Science');
INSERT INTO courses (course_id, course_name) VALUES (4, 'Linear Algebra');插入先修课关系记录:
1
2
3
4
5
6-- 课程 Computer Science 需要 Mathematics 和 Physics 作为先修课
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (3, 1); -- Computer Science -> Mathematics
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (3, 2); -- Computer Science -> Physics
-- 课程 Physics 需要 Linear Algebra 作为先修课
INSERT INTO prerequisites (course_id, prerequisite_id) VALUES (2, 4); -- Physics -> Linear Algebra在上述例子中:
prerequisites表表示课程之间的先修关系。例如,Computer Science课程的course_id是 3,它的先修课是Mathematics(prerequisite_id为 1)和Physics(prerequisite_id为 2)。- 通过这种方式,可以表示一门课程有多门先修课,同时一门课程也可以作为多门课程的先修课。
- 插入的
course_id和prerequisite_id必须都是courses表中已有的课程,否则会插入失败。
删除数据(删)
由于在创建表时设置了级联操作
ON DELETE CASCADE,因此当我们删除任何一个存在的课程时,与该课程相关的所有先修课信息也都会被级联删除。无论该课程是其他课程的先修课,还是它自身有先修课。
2.4 关系代数
用符号表示所有的关系运算逻辑有助于在理论上进行化简,从而降低计算开销。
传统的集合运算
并
专门的关系运算
先补充几个必要的符号表示:
- 元组。在关系 R 中,
t ∈ R t \in R t [ A i ] t[A_i] A i A_i - 取反。针对属性集合 X,取反就是属性全集 U 和属性集合 X 的差。
- 串接。将两个元组左右连接。
- 象集。对于关系
R ( A 1 , A 2 ) R(A_1,A_2) A 1 A_1 A 1 A_1 A 2 A_2
选择
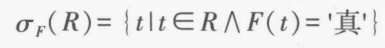
投影
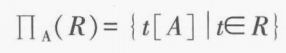
连接

- 一般连接。就是上述所述。
- 左外连接。当 R 的属性 A 的取值不在 S 的 B 中时,在结果中保留 R 的结果,S 对应的值填 NULL。
- 右外连接。当 S 的属性 B 的取值不在 R 的 A 中时,在结果中保留 S 的结果,R 对应的值填 NULL。
除法
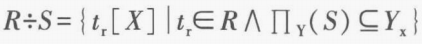
3 SQL
4 安全性
5 完整性
开发篇
关系数据理论
数据库设计
数据库编程 *
这一章不作考试要求。樂。
进阶篇
关系数据库存储管理
关系查询
怎么查询关系的?又可以怎么优化查询策略呢?
数据库恢复技术
并发
]]>前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 杨琬琪 | 3 | 专业课 |
成绩组成:
理论课:
| 作业+课堂 | 课堂测验(2次) | 期末(闭卷) |
|---|---|---|
| 30% | 20% | 50% |
实验课:
| 19次实验(五级制) |
|---|
| 100% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 机器学习与模式识别 | 《机器学习与模式识别》 | – | 周志华 | 清华大学出版社 | 978-7-302-42328-7 |
学习资源:
- 🍉 西瓜书 📺 视频、PPT 资源:机器学习初步、PPT - 百度网盘链接
- 🍉 西瓜书 📖 电子资源:Machine_Learning/机器学习_周志华.pdf
- 🎃 南瓜书 📺 视频资源:《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
- 🎃 南瓜书 📖 电子资源:《机器学习》(西瓜书)公式详解
实验平台:
- AI Studio:https://aistudio.baidu.com/index
本地路径:
- 🍉 西瓜书电子书:[机器学习_周志华](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_周志华.pdf)
- 🎃 南瓜书电子书:[pumpkin_book](D:\华为云盘\2. Score\4. 机器学习与模式识别\pumpkin-book\pdf\pumpkin_book_1.9.9.pdf)
- 📃 上课 PPT by 周志华:[机器学习_课件_周志华](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_课件_周志华)
- 📃 上课 PPT by 杨琬琪:[机器学习_课件_杨琬琪](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_课件_杨琬琪)
第1章 绪论
1.1 引言
pass
1.2 基本术语
| Name | Introduction |
|---|---|
| 机器学习定义 | 利用经验改善系统自身性能,主要研究智能数据分析的理论和方法。 |
| 计算学习理论 | 最重要的理论模型是 PAC(Probably Approximately Correct, 概率近似正确) learning model,即以很高的概率得到很好的模型 $P( |
| P 问题 | 在多项式时间内计算出答案的解 |
| NP 问题 | 在多项式时间内检验解的正确性 |
| 特征(属性) | – |
| 特征(属性)值 | 连续 or 离散 |
| 样本维度 | 特征(属性)个数 |
| 特征(属性、输入)空间 | 特征张成的空间 |
| 标记(输出)空间 | 标记张成的空间 |
| 样本 | <x> |
| 样例 | <x,y> |
| 预测任务 | 监督学习、无监督学习、半监督学习、噪音标记学习、多标记学习 |
| 泛化能力 | 应对未来未见的测试样本的能力 |
| 独立同分布假设 | 历史和未来的数据来自相同的分布 |
1.3 假设空间
假设空间:所有可能的样本组合构成的集合空间
版本空间:根据已知的训练集,将假设空间中与正例不同的、反例一致的样本全部删掉,剩下的样本组合构成的集合空间
1.4 归纳偏好
No Free Launch 理论,没有很好的算法,只有适合的算法。好的算法来自于对数据的好假设、好偏执,大胆假设,小心求证
1.5 发展历程
pass
1.6 应用现状
pass
第2章 模型评估与选择
2.1 经验误差与过拟合
概念辨析
- 错误率:针对测试数据而言,分错的样本数
a a m m E = a m E=\frac{a}{m} - 经验误差:针对训练数据而言,随着训练轮数或模型的复杂度越高,经验误差越小

过拟合解决方法
Early Stopping (当发现有过拟合现象就停止训练)
Penalizing Large Weight (在经验风险上加一个正则化项)
▶正则化概念补充在后面的学习中经常会和正则化打交道,因此此处补充一下相关的概念。
在目标函数中添加正则化到底有什么好处?给几个解释:
- 防止过拟合。为什么可以防止过拟合?其实可以形象化的将添加的正则化项理解为一个可以调节的「累赘」,为了让原始问题尽可能的最优,我让累赘愈发拖累目标函数的取值,这样原始问题就不得不更优以此来抵消累赘带来的拖累。
- 可以进行特征选择。个人认为属于第一点的衍生意义,为什么这么说?同样用累赘来比喻正则化项。当原始问题的某些变量为了代偿拖累导致系数都接近于零了,那么这个变量也就没有存在的意义了,于是对应的特征也就被筛选掉了,也就是所谓的特征选择了。常常添加 L1 正则化项来进行所谓的特征选择。
- 提升计算效率。同样可以理解为第三点的衍生意义,为什么这么说?因为你都把变量筛掉了,那么对应的解空间是不是就相应的大幅度减少了,于是最优解的搜索也就更加快速了。
当然正则化项并非万能的万金油,在整个目标函数中正则化项有这举足轻重的意义,一旦正则化项的系数发生了微小的变动,对于整个模型的影响都是巨大的。因此有时添加正则化项并不一定可以带来泛化性能的提升。
正则化有以下形式:
一般式:
∣ ∣ x ∣ ∣ p k = ( ( ∑ i = 1 m ∣ x i ∣ p ) 1 p ) k ||\mathbf{x}||_p^k = \left ( \left ( \sum_{i=1}^{m}|x_i|^{p} \right)^{\frac{1}{p}} \right)^k L1 正则化:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 m ∣ x i ∣ ||\mathbf{x}||_1 = \sum_{i=1}^m |x_i| L2 正则化:
∣ ∣ x ∣ ∣ 2 2 = ( ( ∑ i = 1 m ∣ x i ∣ 2 ) 1 2 ) 2 = ∑ i = 1 m ∣ x i ∣ 2 \begin{aligned}||\mathbf{x}||_2^2 &= \left ( \left ( \sum_{i=1}^{m}|x_i|^{2} \right)^{\frac{1}{2}} \right)^2 \\&= \sum_{i=1}^{m}|x_i|^{2}\end{aligned}
Bagging 思想 (对同一样本用多个模型投票产生结果)
Boosting 思想 (多个弱分类器增强分类能力,降低偏差)
Dropconnection (神经网络全连接层中减少过拟合的发生)
欠拟合解决方法
决策树:拓展分支
神经网络:增加训练轮数
2.2 评估方法
留出法(hold-out):将数据集分为三个部分,分别为训练集、验证集、测试集。测试集对于训练是完全未知的,我们划分出测试集是为了模拟未来未知的数据,因此当下的任务就是利用训练集和验证集训练出合理的模型来尽可能好的拟合测试集。那么如何使用划分出的训练集和验证集来训练、评估模型呢?就是根据模型的复杂度 or 模型训练的轮数,根据上图的曲线情况来选择模型。
交叉验证法(cross validation):一般方法为 p 次 k 折交叉验证,即 p 次将训练数据随机划分为 k 个大小相似的互斥子集。将其中
k − 1 k-1 1 1 k k 自助法(bootstrapping):有放回采样获得训练集。每轮从数据集
D D m m m m m m D ′ D' 2 3 \frac{2}{3} D ′ D' D − D ′ D-D' ▶测试集占比 1/3 证明过程
2.3 性能度量
2.3.1 回归任务
均方误差:
均方根误差:
首先理解各部分的含义。减数的分子表示预测数据的平方差,减数的分母表示真实数据的平方差。而平方差是用来描述数据离散程度的统计量。
为了保证回归拟合的结果尽可能不受数据离散性的影响,我们通过相除来判断预测的数据是否离散。如果和原始数据离散性差不多,那么商就接近1,R方就接近0,表示性能较差,反之如果比原始数据离散性小,那么商就接近0,R方就接近1,表示性能较优。
2.3.2 分类任务
混淆矩阵

准确率(accuracy):
P = T P + T N T P + F N + F P + T N \displaystyle P=\frac{TP+TN}{TP+FN+FP+TN} 查准率/精度(precision):
P = T P T P + F P \displaystyle P = \frac{TP}{TP+FP} 查全率/召回率(recall):
R = T P T P + F N \displaystyle R = \frac{TP}{TP+FN} F1 度量(F1-score):
F 1 = 2 × P × R P + R \displaystyle F_1 = \frac{2\times P \times R}{P + R} 对于多分类问题,我们可以将该问题分解为多个二分类问题(ps:假设为 n 个)。从而可以获得多个上述的混淆矩阵,那么也就获得了多个
P i P_i R i R_i T P ‾ \overline{TP} F P ‾ \overline{FP} F N ‾ \overline{FN} 宏
- 宏查准率:
m a c r o P = 1 n ∑ i = 1 n P i \displaystyle macroP = \frac{1}{n} \sum_{i=1}^n P_i - 宏查全率:
m a c r o R = 1 n ∑ i = 1 n R i \displaystyle macroR = \frac{1}{n} \sum_{i=1}^n R_i - 宏
F 1 F1 m a c r o F 1 = 2 × m a c r o P × m a c r o R m a c r o P + m a c r o R \displaystyle macroF_1 = \frac{2 \times macroP \times macroR}{macroP+macroR}
- 宏查准率:
微
- 微查准率:
m i c r o P = T P ‾ T P ‾ + F P ‾ \displaystyle microP = \frac{\overline{TP}}{\overline{TP}+\overline{FP}} - 微查全率:
m i c r o R = T P ‾ T P ‾ + F N ‾ \displaystyle microR = \frac{\overline{TP}}{\overline{TP}+\overline{FN}} - 微
F 1 F1 m i c r o F 1 = 2 × m i c r o P × m i c r o R m i c r o P + m i c r o R \displaystyle microF_1 = \frac{2 \times microP \times microR}{microP+microR}
- 微查准率:
P-R 曲线

横纵坐标:横坐标为查全率(Recall),纵坐标为查准率(Precision)
如何产生?我们根据学习器对于每一个样本的预测值(正例性的概率)进行降序排序,然后调整截断点将预测后的样本进行二分类,将截断点之前的所有数据全部认为预测正例,截断点之后的所有数据全部认为预测反例。然后计算两个指标进行绘图。
▶什么分类任务中的是预测值?我们知道学习器得到最终的结果一般不是一个绝对的二值,如 0,1。往往是一个连续的值,比如 [0,1],也就是“正例性的概率”。因此我们才可以选择合适的截断点将所有的样本数据划分为两类。
趋势解读:随着截断点的值不断下降,很显然查全率
R R P P 不同曲线对应学习器的性能度量:曲线与横纵坐标围成的面积衡量了样本预测排序的质量。因此上图中 A 曲线的预测质量比 C 曲线的预测质量高。但是我们往往会遇到比较 A 与 B 的预测质量的情况,由于曲线与坐标轴围成的面积难以计算,因此我们引入了平衡点的概念。平衡点就是查准率与查询率相等的曲线,即
P = R P=R
ROC 曲线与 AUC ⭐
横纵坐标:横坐标为假正例率
F P R = F P F P + T N \displaystyle FPR = \frac{FP}{FP+TN} T P R = T P T P + F N \displaystyle TPR = \frac{TP}{TP+FN} 如何产生?与 P-R 图的产生类似,只不过计算横纵坐标的规则不同,不再赘述。
趋势解读:随着截断点的值不断下降,真正例率与假正例率均会不断上升,因为分子都是从 0 开始逐渐增加的
不同曲线对应学习器的性能度量:AUC 衡量了样本预测的排序质量。AUC 即 ROC 曲线右下方的面积,面积越大则对应的预测质量更高,学习器性能更好。不同于上述引入平衡点的概念,此处的面积我们可以直接计算,甚至 1-AUC 也可以直接计算。
我们定义
AUC \text{AUC} ∑ i = 1 m − 1 ( y i + y i + 1 ) ⋅ ( x i + 1 − x i ) 2 \sum _{i=1}^{m-1} \frac{(y_{i}+y_{i+1}) \cdot (x_{i+1} - x_i)}{2} 我们定义损失函数(
l o s s loss l r a n k = 1 − A U C l_{rank} = 1-AUC 
2.4 比较检验
理论依据:统计假设检验(hypothesis test)
两个学习器性能比较:
交叉验证 t 检验:对于 k 折两个学习期产生的 k 个误差之差,求得其均值
μ \mu σ 2 \sigma ^2 Γ t \Gamma_t Γ t \Gamma_t Γ t = ∣ k μ σ ∣ \Gamma_t = |\frac{\sqrt{k}\mu}{\sigma}| McNemar 检验:对于二分类问题,我们可以得到下方的列联表
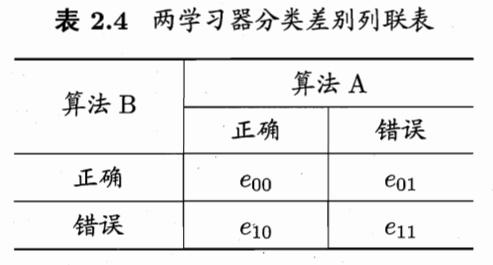
若变量
Γ χ 2 \Gamma_{\chi ^2} Γ χ 2 \Gamma_{\chi ^2} Γ χ 2 = ( ∣ e 01 − e 10 ∣ − 1 ) 2 e 01 + e 10 \Gamma_{\chi ^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01}+e_{10}}
2.5 偏差与方差
现在我们得到了学习算法的泛化性能,我们还想知道为什么会有这样的泛化性能,即我们应该如何理论的解释这样的泛化性能呢?我们引入 偏差-方差分解 的概念来从理论的角度解释期望泛化误差。那么这个方法一定是完美解释的吗?也有一定的缺点,因此我们还会引入 偏差-方差窘境 的概念来解释偏差和方差对于泛化误差的贡献。
在此之前我们需要知道偏差、方差和噪声的基本定义:
- 偏差:学习算法的期望输出与真实结果的偏离程度,刻画算法本身的拟合能力。
- 方差:使用同规模的不同训练集进行训练时带来的性能变化,刻画数据扰动带来的影响。
- 噪声:当前任务上任何算法所能达到的期望泛化误差的下界(即不可能有算法取得更小的误差),刻画问题本身的难度。
2.5.1 偏差-方差分解
我们定义以下符号:
我们以回归任务为例:(下面的全部变量均为在所有相同规模的训练集下得到的期望结果)
- 输出:
f ‾ ( x ) = E D [ f ( x ; D ) ] \overline{f}(x) = E_D[f(x;D)] - 方差:
v a r ( x ) = E D [ ( f ‾ ( x ) − f ( x ; D ) ) 2 ] var(x) = E_D[(\overline{f}(x) - f(x;D))^2] - 偏差:
b i a s 2 ( x ) = ( f ‾ ( x ) − y ) 2 bias^2(x) = (\overline{f}(x) - y)^2 - 噪声:
ϵ 2 = E D [ ( y D − y ) 2 ] \epsilon ^2 = E_D[(y_D - y)^2]
偏差-方差分解的结论:
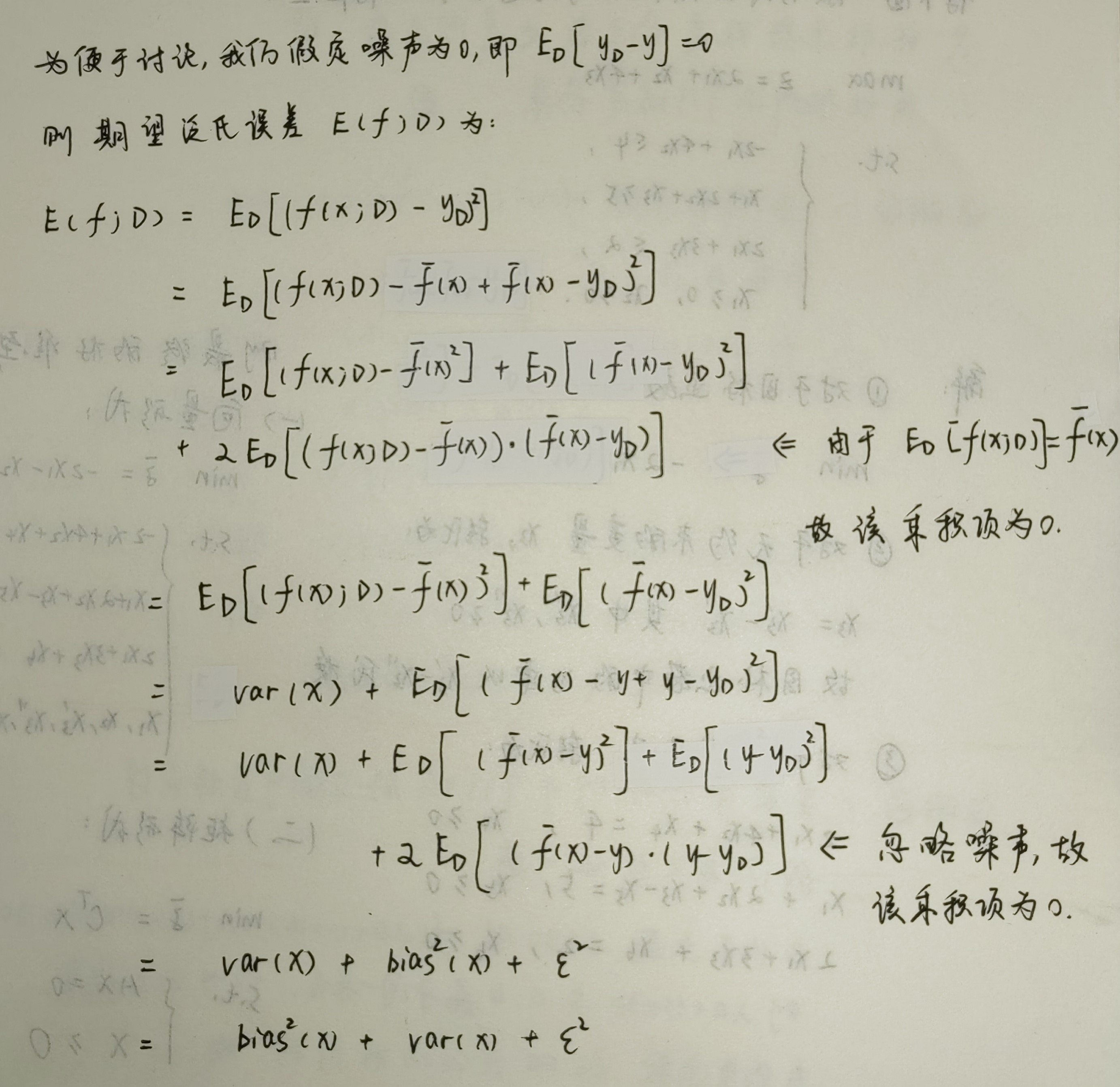
解释说明:泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定的。因此给定一个学习任务,我们可以从偏差和方差两个角度入手进行优化,即需要使偏差较小(充分拟合数据),且需要使方差较小(使数据扰动产生的影响小)
2.5.2 偏差-方差窘境
其实偏差和方差是有冲突的,这被称为偏差-方差窘境(bias-variance-dilemma)。对于以下的示意图我们可以知道:对于给定的学习任务。一开始拟合能力较差,学习器对于不同的训练数据不够敏感,此时泛化错误率主要来自偏差;随着训练的不断进行,学习器的拟合能力逐渐增强,对于数据的扰动更加敏感,使得方差主导了泛化错误率;在训练充分以后,数据的轻微扰动都可能导致预测输出发生显著的变化,此时方差就几乎完全主导了泛化错误率。

第3章 线性模型
本章介绍机器学习模型之线性模型,将从学习任务展开。学习任务分别为:
- 回归(最小二乘法、岭回归)
- 二分类(对数几率(逻辑)回归、线性判别分析)
- 多分类(一对一、一对其余、多对多)
3.1 基本形式
线性模型的优点:形式简单、易于建模、高可解释性、非线性模型的基础
线性模型的缺点:线性不可分
3.2 线性回归
预测式已经在 3.1 中标明了,现在的问题就是,如何获得
在正式开始介绍求解参数
基于均方误差最小化的模型求解方法被称为 最小二乘法 (least squre method)。而求解
于是问题就转化为了无约束的最优化问题求解。接下来我们将从一元线性回归引入,进而推广到多维线性回归的参数求解,最后补充广义的线性回归与其他线性回归的例子。
3.2.1 一元线性回归
现在假设只有一个属性 x,对应一维输出 y。现在我们试图根据已知的 <x,y> 样本数据学习出一个模型
前置说明:在机器学习中,很少有闭式解(解析解),但是线性回归是特例,可以解出闭式解。
闭式解推导过程:
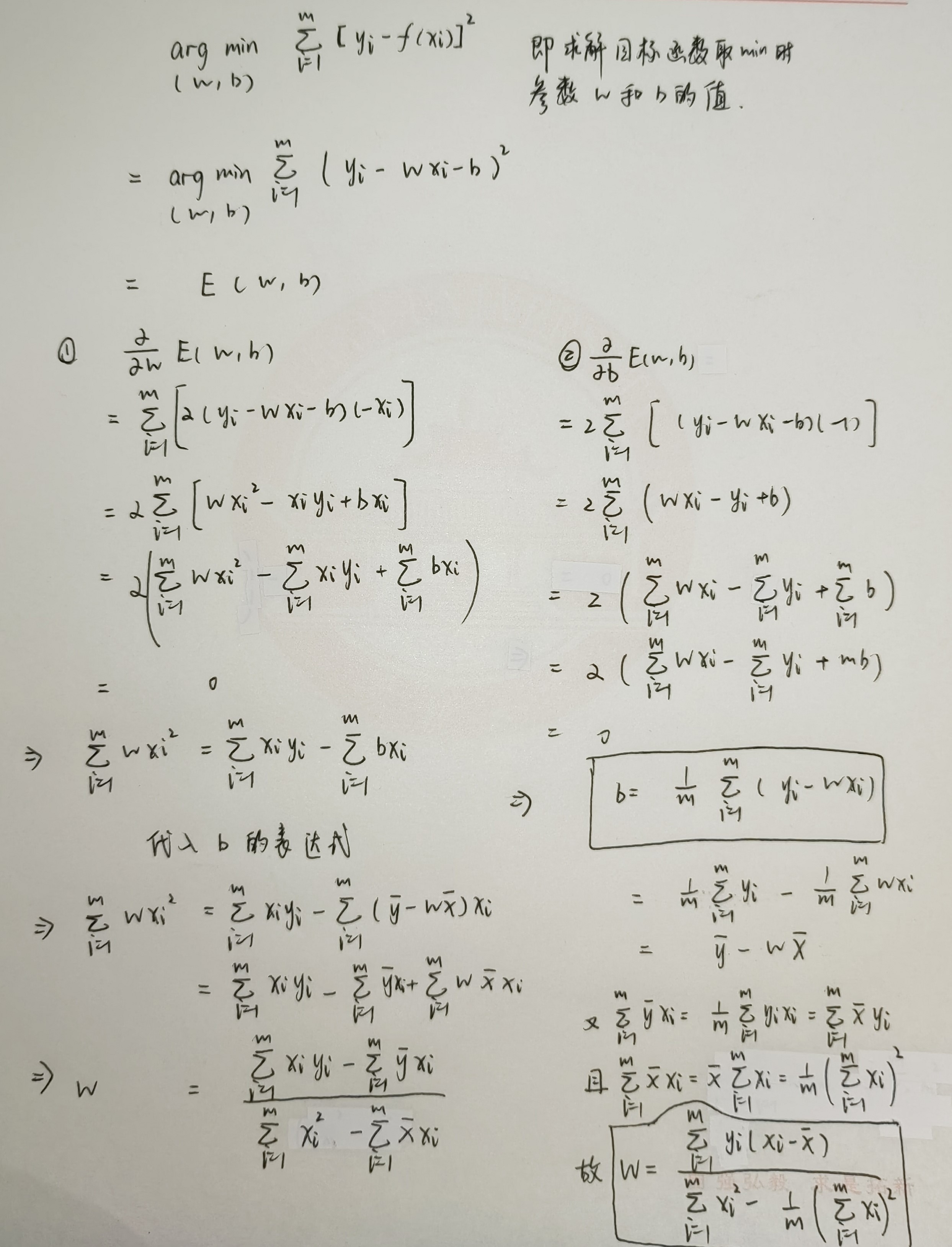
3.2.2 多元线性回归
现在我们保持输出不变,即
现在我们按照原来的方法进行求解。在求解之前我们采用向量的方式简化一下数据的表示,
于是损失函数
我们用同样的方法求解其闭式解:

我们不能直接等式两边同
X T X X^T X w ^ ∗ = ( X T X ) − 1 X T y \hat w ^* = (X^TX)^{-1}X^Ty x ^ i = ( x i , 1 ) \hat x_i = (x_i,1) f ( x i ) = x ^ i T w ^ ∗ f(x_i) = \hat x_i ^T \hat w^* X T X X^T X L 2 L_2 α ∣ ∣ w ^ ∣ ∣ 2 \alpha || \hat w ||^2 现在的损失函数就定义为:
E w ^ = ( y − X w ^ ) T ( y − X w ^ ) + α ∣ ∣ w ^ ∣ ∣ 2 E_{\hat w} = (y - X \hat w) ^T (y - X \hat w) + \alpha || \hat w ||^2 同样将损失函数对参数向量
w ^ \hat w ∂ E w ^ ∂ w ^ = ⋯ = 2 X T X w ^ − 2 X T y + 2 α w ^ = 2 X T ( X w ^ − y ) + 2 α w ^ \begin{aligned}\frac{\partial E_{\hat w}}{\partial \hat w} &= \cdots \\&= 2X^TX\hat w - 2 X^T y + 2 \alpha \hat w \\&= 2 X ^T(X \hat w - y) + 2 \alpha \hat w\end{aligned} 我们令其为零,得参数向量
w ^ \hat w w ^ = ( X T X + α I ) − 1 X T y \hat w = (X^T X + \alpha I)^{-1} X^T y
3.2.3 广义线性回归
可否令模型的预测值
本质上我们训练的线性模型
此时得到的线性模型
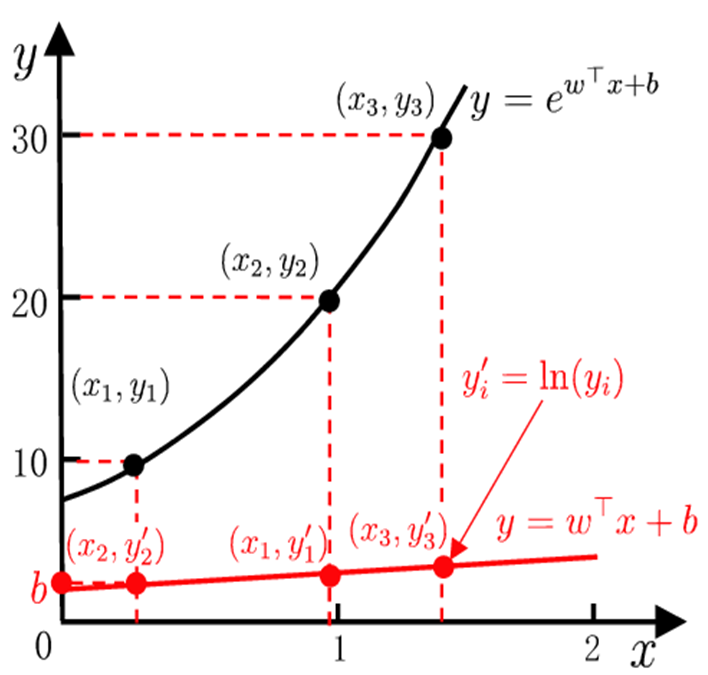
3.2.4 其他线性回归
支持向量机回归
决策树回归
随机森林回归
LASSO 回归:增加
L 1 L_1 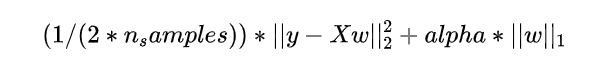
ElasticNet 回归:增加
L 1 L_1 L 2 L_2 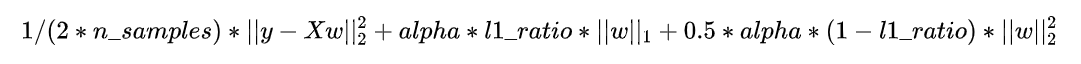
XGBoost 回归
3.3 对数几率回归
对数几率回归准确来说应该叫逻辑回归,并且不是回归的学习任务,而是二分类的学习任务。本目将从阈值函数的选择和模型参数的求解两个维度展开讲解。
3.3.1 阈值函数的选择
对于二分类任务。我们可以将线性模型的输出结果
最简单的一种阈值函数就是单位阶跃函数。映射关系如下。但是有一个问题就是单位阶跃函数不是单调可微函数,因此不可取
▶为什么阈值函数需要单调可微呢?一直有一个疑问,单位跃阶函数已经可以将线性模型的进行二值映射了,干嘛还要求阈值函数的反函数呢?
其实是因为知道的太片面了。我们的终极目的是为了通过训练数据,学习出线性模型中的
w w b b z = w T x + b z=w^Tx+b g ( ⋅ ) g(\cdot) y = g ( z ) y=g(z) w w b b E ( w , b ) = ∑ i = 1 m ( y i − g ( x i ) ) 2 E_{(w,b)} = \sum_{i=1}^m (y_i - g(x_i))^2 g ( ⋅ ) g(\cdot) 至此疑问解决!让我们畅快的学习单调可微的阈值函数吧!
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 y = \begin{cases}0, &z < 0 \\0.5,& z=0 \\1, & z>0\end{cases} 常用的一种阈值函数是对数几率函数,也叫逻辑函数(
logistic function \text{logistic function} y = 1 1 + e − z y = \frac{1}{1+e^{-z}}
3.3.2 模型参数的求解
现在我们站在前人的肩膀上学习到了一种阈值函数:逻辑函数(
这就要从逻辑函数的实际意义出发了。对于逻辑函数,我们代入线性模型,并做以下转化:
若我们定义
知道了逻辑函数的实际意义是真实标记的对数几率以后,接下来我们实际意义出发,讲解模型参数
若我们将
同时,显然有
于是我们可以确定目标函数了。我们取当前目标函数为对数似然函数:
显然的,当上述目标函数取最大值时,得到的参数
我们将变量进行一定的变形:
于是上述对数似然函数就可以进行以下转化:
进而从极大似然估计转化为:求解「极小化负的上述目标函数时」参数
由于上式是关于
目标函数:
第
其中
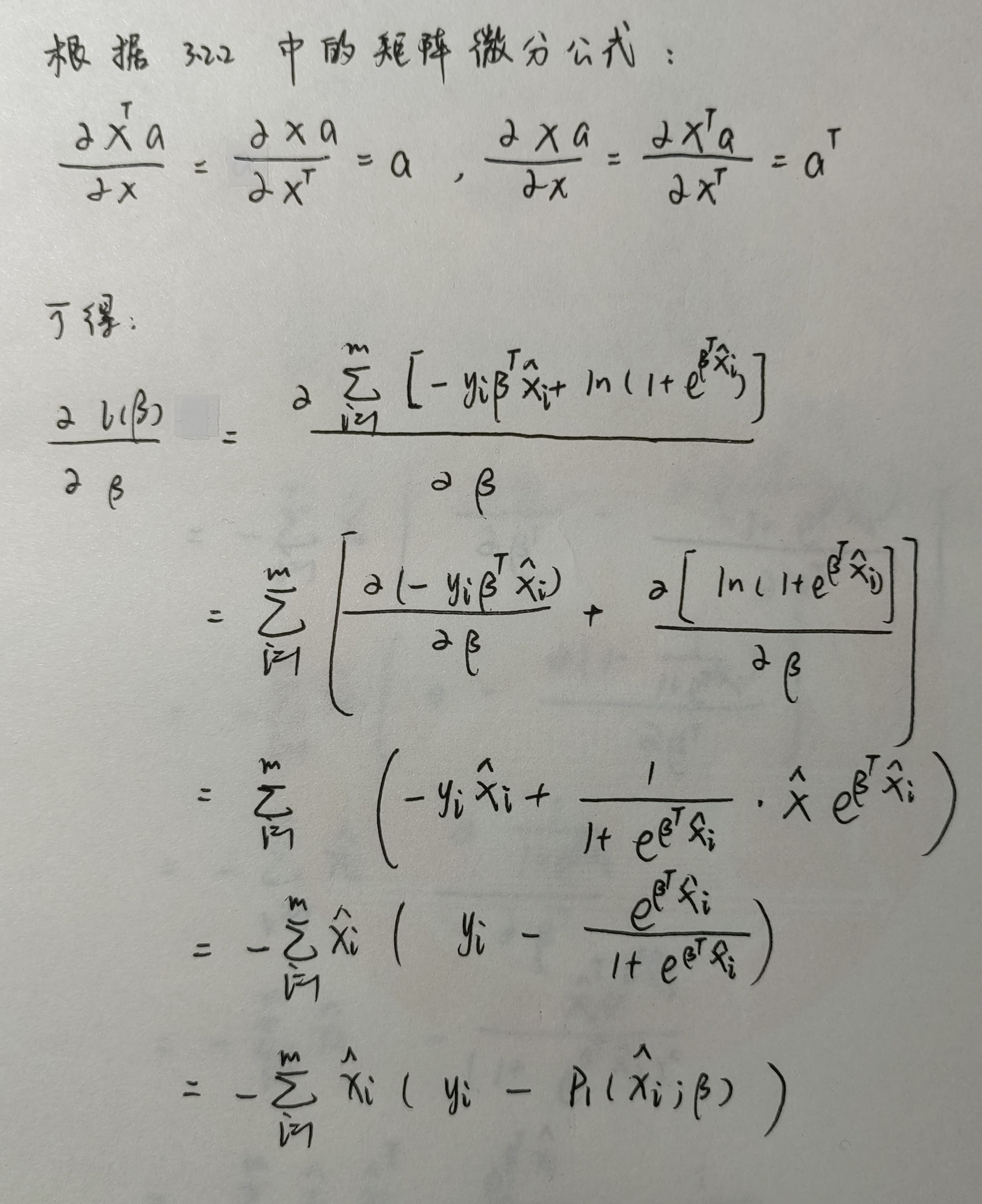
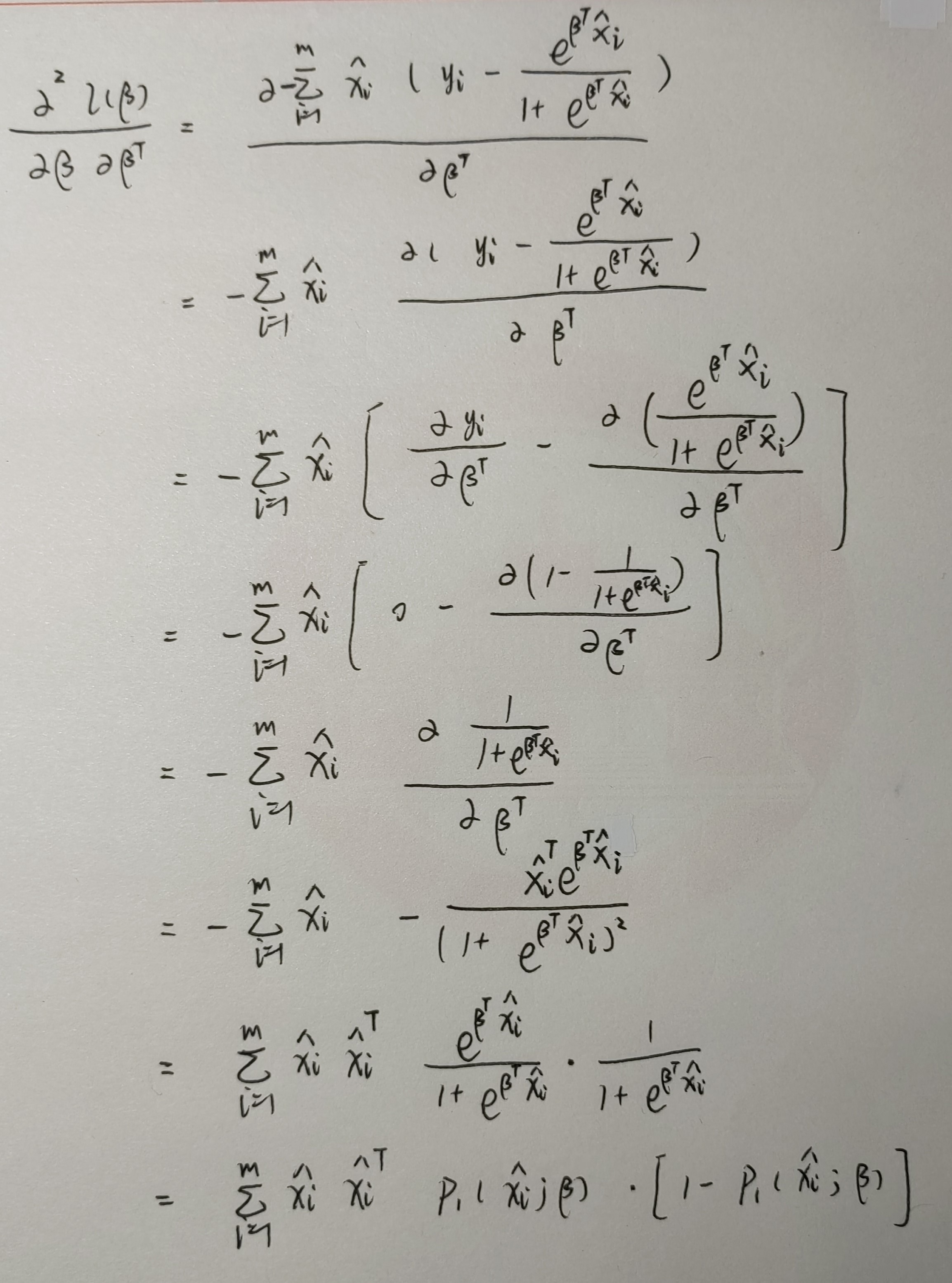
3.4 线性判别分析
线性判别分析的原理是:对于给定的训练集,设法将样本投影到一条直线上,使得同类的投影点尽可能接近,异类样本的投影点尽可能远离;在对新样本进行分类时,将其投影到这条直线上,再根据投影点的位置来确定新样本的类别。
3.5 多分类学习
我们一般采用多分类+集成的策略来解决多分类的学习任务。具体的学习任务大概是:将多分类任务拆分为多个二分类任务,每一个二分类任务训练一个学习器;在测试数据时,将所有的分类器进行集成以获得最终的分类结果。这里有两个关键点:如何拆分多分类任务?如何集成二分类学习器?集成策略见第 8 章,本目主要介绍多分类学习任务的拆分。主要有三种拆分策略:一对多、一对其余、多对多。对于 N 个类别而言:
3.5.1 一对一
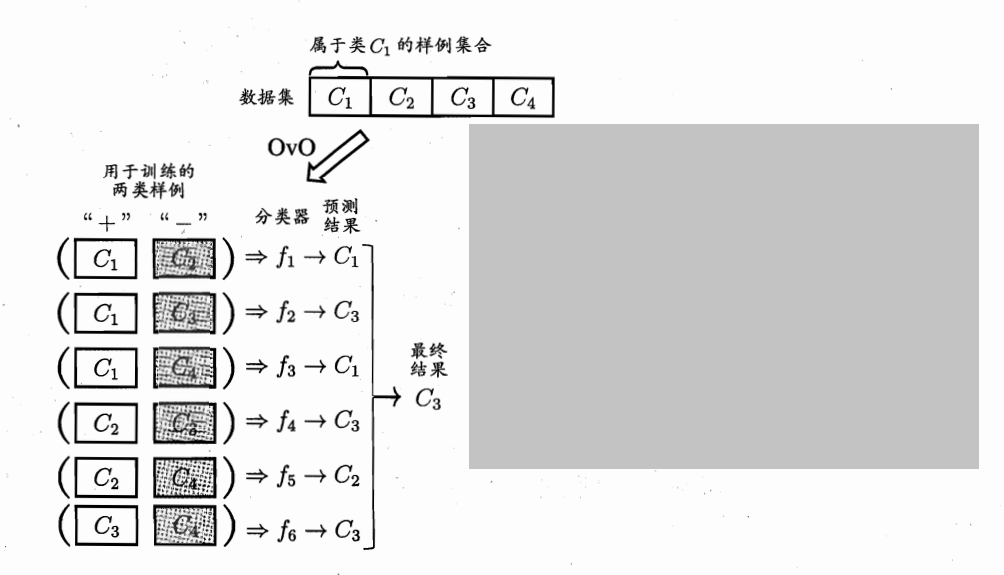
- 名称:One vs. One,简称 OvO
- 训练:需要对 N 个类别进行
N ( N − 1 ) 2 \frac{N(N-1)}{2} N ( N − 1 ) 2 \frac{N(N-1)}{2} - 测试:对于一个样本进行分类预测时,需要用
N ( N − 1 ) 2 \frac{N(N-1)}{2} - 特点:类别较少时,时间和内存开销往往更大;类别较多时,时间开销往往较小
3.5.2 一对其余
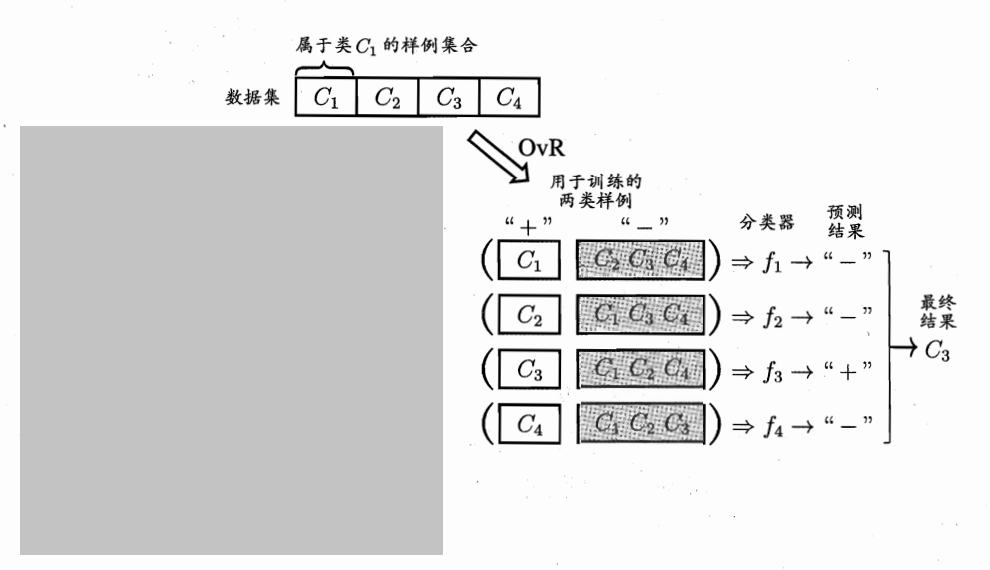
- 名称:One vs. Rest,简称 OvR
- 训练:需要对 N 个类别进行
N N N N - 测试:对于一个样本进行分类预测时,需要用
N N N N
3.5.3 多对多
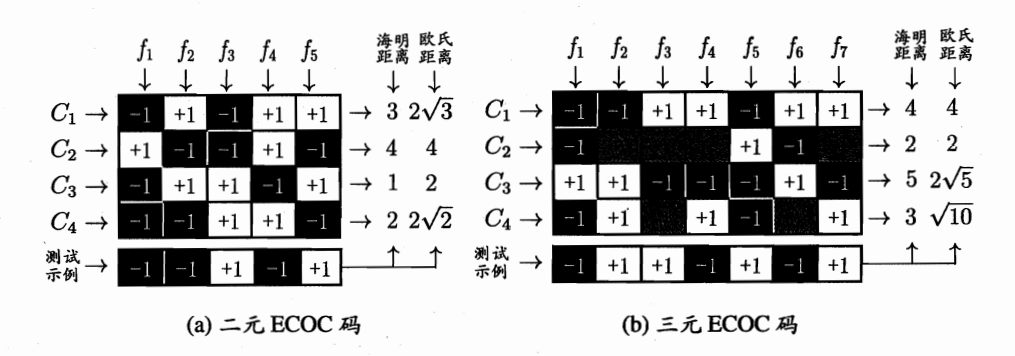
- 名称:Many vs. Many,简称 MvM
- 训练(编码):对于 N 个类别数据,我们自定义 M 次划分。每次选择若干个类别作为正类,其余类作为反类。每一个样本在 M 个二分类学习器中都有一个分类结果,也就可以看做一个 M 维的向量。m 个样本也就构成了 m 个在 M 维空间的点阵。
- 测试(解码):对于测试样本,对于 M 个学习器同样也会有 M 个类别标记构成的向量,我们计算当前样本与训练集构造的 m 个样本的海明距离、欧氏距离,距离当前测试样本最近的点属于的类别,我们就认为是当前测试样本的类别。
3.5.4 softmax
类似于 M-P 神经元,目的是为了将当前测试样本属于各个类别的概率之和约束为 1。
3.6 类别不平衡问题
在分类任务的数据集中,往往会出现类别不平衡的问题,即使在类别的样本数量相近时,在使用一对其余等算法进行多分类时,也会出现类比不平衡的问题,因此解决类比不平衡问题十分关键。
3.6.1 阈值移动
常规而言,对于二分类任务。我们假设
但是显然,上述假设不总是成立,我们令
根本初衷是为了让
3.6.2 欠采样
即去除过多的样本使得正反例的数量近似,再进行学习。
- 优点:训练的时间开销小
- 缺点:可能会丢失重要信息
典型的算法是:EasyEnsemble
3.6.3 过采样
即对训练集中类别数量较少的样本进行重复采样,再进行学习。
- 缺点:简单的重复采样会导致模型过拟合数据,缺少泛化能力。
典型的算法是:SMOTE
第4章 决策树
4.1 基本流程
决策树算法遵循自顶向下、分而治之的思想。
决策树结构解读:
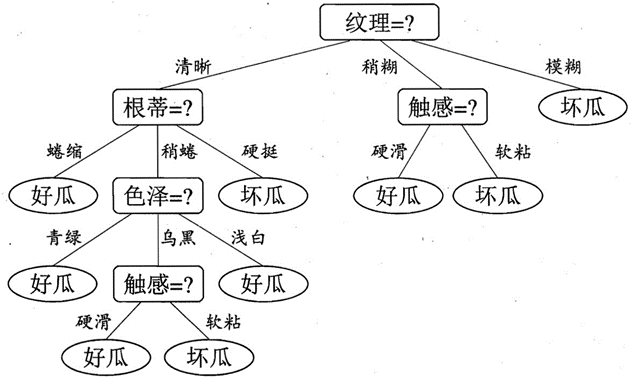
- 非叶子结点:属性
- 边:属性值
- 叶子结点:分类结果
决策树生成过程:

- 生成结点:选择最优的属性作为当前结点决策信息
- 产生分支:根据结点属性,为测试数据所有可能的属性值生成一个分支
- 生成子结点:按照上述分支属性对当前训练样本进行划分
- 不断递归:不断重复上述 1-3 步直到递归终点
- 递归终点:共三种(存疑)
- 当前结点的训练样本类别均属于某个类别。则将当前结点设定为叶子结点,并标记当前叶子结点对应的类别为当前结点同属的类别
- 当前结点的训练样本数为
0 0 - 当前结点的训练样本的所有属性值都相同。则将当前结点设定为叶子结点,并标记当前叶子结点对应的类别为当前训练样本中最多类别数量对应的类别
4.2 划分选择
现在我们解决 4.1 节留下的坑,到底如何选择出当前局面下的最优属性呢?我们从“希望当前结点的所包含的样本尽可能属于同一类”的根本目的出发,讨论三种最优属性选择策略。
4.2.1 信息增益
第一个问题:如何度量结点中样本的纯度? 我们引入 信息熵 (information entropy) 的概念。显然,信息熵越小,分支结点的纯度越高;信息熵越大,分支结点的纯度越低。假设当前样本集合中含有
第二个问题:如何利用结点纯度选择最优属性进行划分? 我们引入 信息增益 (Information gain) 的概念。显然,我们需要计算每一个属性对应的信息增益,然后取信息增益最大的属性作为当前结点的最优划分属性。假设当前结点对应的训练数据集为
代表算法:ID3
为了更好的理解信息增益的表达式,我们从终极目标考虑问题。我们知道,决策树划分的终极目的是尽可能使得子结点中的样本纯度尽可能高。对于当前已知的结点,信息熵已经是一个定值了,只有通过合理的划分子结点才能使得整体的熵减小,因此我们从划分后熵减的理念出发,得到了信息增益的表达式。并且得出熵减的结果(信息增益)越大,对应的属性越优。
4.2.2 增益率
由于信息增益会在属性的取值较多时有偏好,因此我们引入 增益率 (Gain ratio) 的概念来减轻这种偏好。显然,增益率越大越好
我们定义增益率为:
可以看到就是将信息增益除上了一个值
一般而言,属性的属性取值越多,信息增益越大,对应的
代表算法:C4.5
4.2.3 基尼指数
最后引入一种最优划分策略:使用 基尼指数 (Gini index) 来划分。基尼指数越小越好。假设当前样本集合中含有
于是属性
代表算法:CART
4.3 剪枝处理
处理过拟合的策略:剪枝。
4.3.1 预剪枝
基于贪心的思想,决策每次划分是否需要进行。我们知道最佳属性的选择是基于信息增益等关于结点纯度的算法策略,而是否进行子结点的生成需要我们进行性能评估,即从测试精度的角度来考虑。因此决策划分是否进行取决于子结点生成前后在验证集上的测试精度,如果可以得到提升则进行生成,反之则不生成子结点,也就是预剪枝的逻辑。
4.3.2 后剪枝
同样是预剪枝的精度决策标准。我们在一个决策树完整生成以后,从深度最大的分支结点开始讨论是否可以作为叶子结点,也就是是否删除该分支的子结点。决策的依据是删除子结点前后在测试集上的精度是否有提升,如果有则删除子结点,反之不变。
4.3.3 区别与联系(补)
预剪枝是基于贪心,也就是说没有考虑到全局的情况,可能出现当前结点划分后测试精度下降,但是后续结点继续划分会得到性能提升,从而导致预剪枝的决策树泛化性能下降。
后剪枝就可以规避贪心导致的局部最优。但是代价就是时间开销更大。
4.4 连续与缺失值
4.4.1 连续值处理
这里讲解二分法 (bi-partition)。主要就是在计算信息增益时增加了一步,将属性的取值情况划分为了两类。那么如何划分呢?关键在于划分点的取值。假设当前属性 a 的取值是连续值,去重排序后得到 n 个数值,我们取这 n 个数值的 n-1 个间隔的中值作为划分点集合,枚举其中的每一个划分点计算最大信息增益,对应的划分点就是当前连续取值的属性的二分划分点。时间复杂度极高!也不知道 C4.5 算法怎么想的
4.4.2 缺失值处理
当然我们可以直接删除含有缺失信息的样本,但是这对数据信息过于浪费,尤其是当数据量不大时,如何解决这个问题呢?我们需要解决两个问题:
- 在选择最优划分属性时,如何计算含有缺失值的属性对应的信息增益呢?
- 在得到最优划分属性时,如何将属性值缺失的样本划分到合理的叶子结点呢?
对于第一个问题:只计算属性值没有缺失的样本,然后放缩到原始的数据集合大小即可
对于第二个问题:对于已知属性值的样本,我们可以计算出每一个属性值的样本数量,从而计算出一个集合比例,这样对于未知属性值的样本,只需要按照前面计算出来的集合,按照概率划分到对应的子结点即可
4.5 多变量决策树
很好,本目就是来解决上述连续值处理的过高时间复杂度的问题的。现在对于一个结点,不是选择最优划分属性,而是对建一个合适的线性分类器,如图:
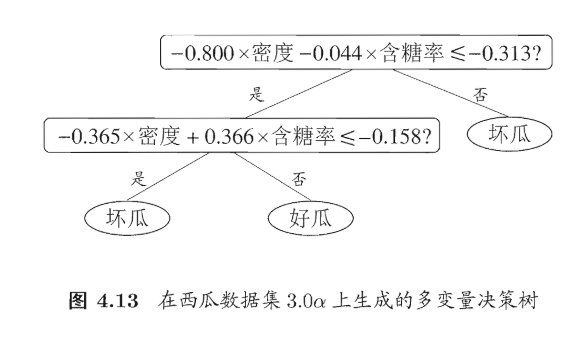
第5章 神经网络
5.1 神经元模型
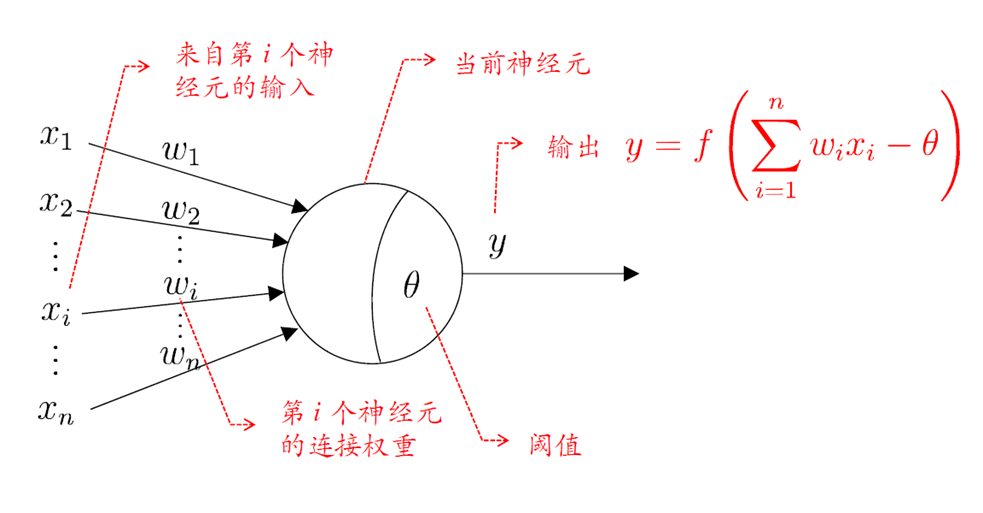
我们介绍 M-P 神经元模型。该神经元模型必须具备以下三个特征:
- 输入:来自其他连接的神经元传递过来的输入信号
- 处理:输入信号通过带权重的连接进行传递,神经元接受到所有输入值的总和,再与神经元的阈值进行比较
- 输出:通过激活函数的处理以得到输出
激活函数可以参考 3.3 中的逻辑函数(logistic function),此处将其声明为 sigmoid 函数,同样不采用不。连续光滑的分段函数。
5.2 感知机与多层网络
本目从无隐藏层的感知机出发,介绍神经网络在简单的线性可分问题上的应用;接着介绍含有一层隐藏层的多层感知机,及其对于简单的非线性可分问题上的应用;最后引入多层前馈神经网络模型的概念。
5.2.1 感知机
感知机(Perceptron)由两层神经元组成。第一层是输入层,第二层是输出层。其中只有输出层的神经元为功能神经元,也即 M-P 神经元。先不谈如何训练得到上面的
通过单层的感知机,我们可以实现简单的线性可分的分类任务,比如逻辑运算中的 与、或、非 运算,下面演示一下如何使用单层感知机实现上述三种逻辑运算:
与运算、或运算是二维线性可分任务,一定可以找到一条直线将其划分为两个类别:
非运算是一维线性可分任务,同样也可以找到一条直线将其划分为两个类别:

5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权

5.2.3 多层前馈神经网络

所谓多层前馈神经网络,定义就是各层神经元之间不会跨层连接,也不存在同层连接,其中:
- 输入层仅仅接受外界输入,没有函数处理功能
- 隐藏层和输出层进行函数处理
5.3 误差逆传播算法
多层网络的学习能力比感知机的学习能力强很多。想要训练一个多层网络模型,仅仅通过感知机的参数学习规则是不够的,我们需要一个全新的、更强大的学习规则。这其中最优秀的就是误差逆传播算法(errorBackPropagation,简称 BP),往往用它来训练多层前馈神经网络。下面我们来了解一下 BP 算法的内容、参数推导与算法流程。
5.3.1 模型参数
我们对着神经网络图,从输入到输出进行介绍与理解:
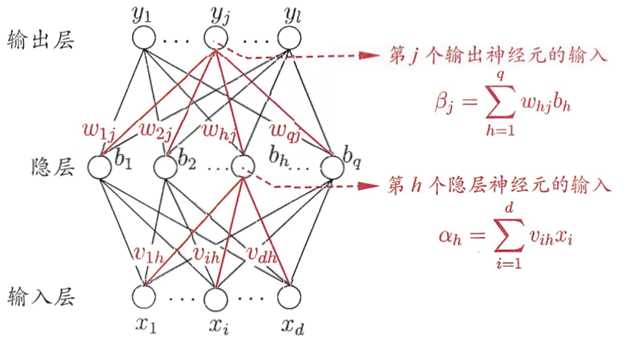
- 隐层:对于隐层的第
h h - 输入:
α h = ∑ i = 1 d x i v i h \alpha_h = \sum_{i=1}^dx_i v_{ih} - 输出:
b h = f ( α h − γ h ) b_h = f(\alpha_h - \gamma_h)
- 输入:
- 输出层:对于输出层的第
j j - 输入:
β j = ∑ h = 1 q b h w h j \beta_j=\sum_{h=1}^q b_h w_{hj} - 输出:
y ^ j = f ( β j − θ j ) \hat y_j = f(\beta j - \theta_j)
- 输入:
现在给定一个训练集学习一个分类器。其中每一个样本都含有
- 输入层到隐层的
d × q d \times q v i h ( i = 1 , 2 , ⋯ , d , h = 1 , 2 , ⋯ , q ) v_{ih}(i=1,2,\cdots,d,\ h=1,2,\cdots,q) - 隐层的
q q γ h ( h = 1 , 2 , ⋯ , q ) \gamma_h(h=1,2,\cdots,q) - 隐层到输出层的
q × l q\times l w h j ( h = 1 , 2 , ⋯ , q , j = 1 , 2 , ⋯ , l ) w_{hj}(h=1,2,\cdots,q,\ j=1,2,\cdots,l) - 输出层的
l l θ j ( j = 1 , 2 , ⋯ , l ) \theta_j(j=1,2,\cdots,l)
5.3.2 参数推导
确定损失函数。
对于上述 4 种参数,我们均采用梯度下降策略。以损失函数的负梯度方向对参数进行调整。每次输入一个训练样本,都会进行一次参数迭代更新,这叫标准 BP 算法。
根本目标是使损失函数尽可能小,我们定义损失函数
E E 1 2 \frac{1}{2} k k
确定迭代修正量。
假定当前学习率为
η \eta w h j ← w h j + Δ w h j θ j ← θ j + Δ θ j v i h ← v i h + Δ v i h γ h ← γ h + Δ γ h \begin{aligned}w_{hj} &\leftarrow w_{hj}+\Delta w_{hj} \\\theta_{j} &\leftarrow \theta_{j}+\Delta \theta_{j} \\v_{ih} &\leftarrow v_{ih}+\Delta v_{ih} \\\gamma_{h} &\leftarrow \gamma_{h}+\Delta \gamma_{h} \\\end{aligned} 其中,修正量分别为:
Δ w h j = η g j b h Δ θ j = − η g j Δ v i h = η e h x i Δ γ h = − η e h \begin{aligned}\Delta w_{hj} &= \eta g_j b_h \\\Delta \theta_{j} &= -\eta g_j \\\Delta v_{ih} &= \eta e_h x_i \\\Delta \gamma_{h} &= -\eta e_h \\\end{aligned}
公式表示:

隐层到输出层的权重、输出神经元的阈值:

输入层到隐层的权重、隐层神经元的阈值:

5.3.3 算法流程
对于当前样本的输出损失

还有一种 BP 神经网络方法就是累计 BP 神经网络算法,基本思路就是对于全局训练样本计算累计误差,从而更新参数。在实际应用过程中,一般先采用累计 BP 算法,再采用标准 BP 算法。还有一种思路就是使用随机 BP 算法,即每次随机选择一个训练样本进行参数更新。
第6章 支持向量机
依然是分类学习任务。我们希望找到一个超平面将训练集中样本划分开来,那么如何寻找这个超平面呢?下面开始介绍。
本章知识点逻辑链:

6.1 间隔与支持向量
对于只有两个特征,输出只有两种状态的训练集而言,很显然我们得到如下图所示的超平面,并且显然应该选择最中间的泛化能力最强的那一个超平面:

我们定义超平面为:
定义支持向量机为满足下式的样例:
很显然,为了求得这“最中间”的超平面,就是让异类支持向量机之间的距离尽可能的大,根据两条平行线距离的计算公式,可知间隔为:
于是最优化目标函数就是:
可以等价转化为:
这就是 SVM(support vector machine)的基本型
6.2 对偶问题
将上述 SVM 基本型转化为对偶问题,从而可以更高效的求解该最优化问题。


于是模型
其中参数 b 的求解可通过支持向量得到:
由于原问题含有不等式约束,因此还需要满足 KKT 条件:
对于上述互补松弛性:
- 若
α i > 0 \alpha_i > 0 y i f ( x i ) = 1 y_if(x_i)=1 - 若
y i f ( x i ) > 1 y_if(x_i)>1 α i = 0 \alpha_i = 0
现在得到的对偶问题其实是一个二次规划问题,我们可以采用 SMO(Sequential Minimal Optimization) 算法求解。具体略。
6.3 核函数
对原始样本进行升维,即

表格中的高斯核也就是所谓的径向基函数核
- 当
γ \gamma exp ( − γ ∥ x i − x j ∥ 2 ) \exp(-\gamma \|x_i - x_j\|^2) - 当
γ \gamma exp ( − γ ∥ x i − x j ∥ 2 ) \exp(-\gamma \|x_i - x_j\|^2)
6.4 软间隔与正则化
对于超平面的选择,其实并不是那么容易,并且即使训练出了一个超平面,我们也不知道是不是过拟合产生的,因此我们需要稍微减轻约束条件的强度,因此引入软间隔的概念。
我们定义软间隔为:某些样本可以不严格满足约束条件
常见的平滑连续的替代损失函数为:

我们引入松弛变量
6.5 支持向量回归
支持向量回归(Support Vector Regression,简称 SVR)与传统的回归任务不同,传统的回归任务需要计算每一个样本的误差,而支持向量回归允许有一定的误差,即,仅仅计算落在隔离带外面的样本损失。
原始问题:


对偶问题:
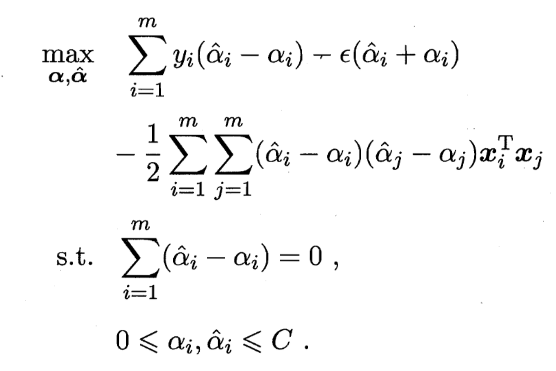
KKT 条件:
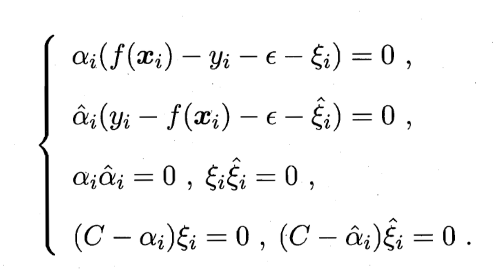
预测模型:

6.6 核方法
通过上述:支持向量基本型、支持向量软间隔化、支持向量回归,三个模型的学习,可以发现最终的预测模型都是关于核函数与拉格朗日乘子的线性组合,那么这是巧合吗?并不是巧合,这其中其实有一个表示定理:
第7章 贝叶斯分类器
7.1 贝叶斯决策论
pass
7.2 极大似然估计
根本任务:寻找合适的参数
我们定义对数似然
此时参数
7.3 朴素贝叶斯分类器
我们定义当前类别为
现在假设各属性之间相互独立,则对于拥有 d 个属性的训练集,在利用贝叶斯定理时,可以通过连乘的形式计算类条件概率
注意点:
- 对于离散数据。上述类条件概率的计算方法很好计算,直接统计即可
- 对于连续数据。我们就没法直接统计数据数量了,替换方法是使用高斯函数。我们根据已有数据计算得到一个对于当前属性的高斯函数,后续计算测试样例对应属性的条件概率,代入求得的高斯函数即可。
- 对于类条件概率为 0 的情况。我们采用拉普拉斯修正。即让所有属性的样本个数
+ 1 +1 + d +d 1 1
7.4 半朴素贝叶斯分类器
朴素贝叶斯的问题是假设过于强,现实不可能所有的属性都相互独立。半朴素贝叶斯弱化了朴素贝叶斯的假设。现在假设每一个属性最多只依赖一个其他属性。即独依赖估计
如何寻找依赖关系?我们从属性依赖图出发
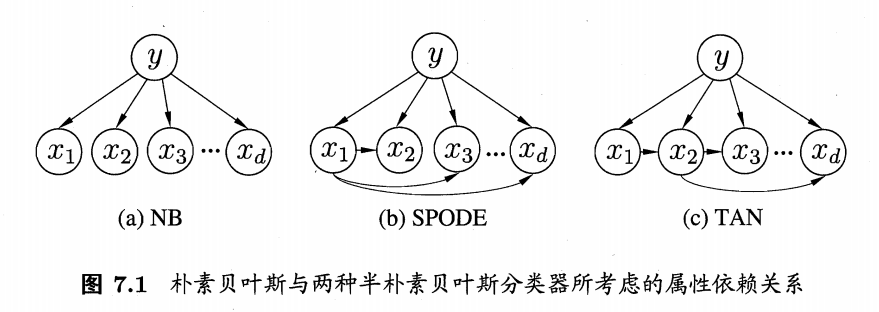
如上图所示:
- 朴素贝叶斯算法中:假设所有属性相互独立,因此各属性之间没有连边
- SPODE 确定属性父属性算法中:假设所有属性都只依赖于一个属性(超父),我们只需要找到超父即可
- TAN 确定属性父属性算法中:我们需要计算每一个属性之间的互信息,最后得到一个以互信息为边权的完全图。最终选择最大的一些边构成一个最大带权生成树
- AODE 确定属性父属性算法中:采用集成的思想,以每一个属性作为超父属性,最后选择最优即可
7.5 贝叶斯网
构造一个关于属性之间的 DAG 图,从而进行后续类条件概率的计算。三种典型依赖关系:
| 同父结构 | V型结构 | 顺序结构 |
|---|---|---|
 |  |  |
| 在已知 | 若 | 在已知 |
概率计算公式参考:超详细讲解贝叶斯网络(Bayesian network)
7.6 EM 算法
现在我们需要解决含有隐变量
- E-step:首先利用观测数据
X X Θ t \Theta_t Z t Z^t - M-step:接着对
X X Z t Z^t Θ t + 1 \Theta_{t+1}
有两个问题:哪来的参数?什么时候迭代终止?
- 对于第一个问题:我们随机化初始得到参数
Θ 0 \Theta_0 - 对于第二个问题:相邻两次迭代结果中参数差值的范数小于阈值
( ∣ ∣ θ ( i + 1 ) − θ ( i ) ) ∣ ∣ < ϵ 1 ) (|| \theta^{(i+1)} - \theta^{(i)}) || < \epsilon_1) ( ∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ < ϵ 2 ) (|| Q(\theta^{(i+1)} , \theta^{(i)})) - Q(\theta^{(i)} , \theta^{(i)}) || < \epsilon_2)
第8章 集成学习
8.1 个体与集成
集成学习由多个不同的组件学习器组合而成。学习器不能太坏并且学习器之间需要有差异。如何产生并结合“好而不同”的个体学习器是集成学习研究的核心。集成学习示意图如下:
根据个体学习器的生成方式,目前集成学习可分为两类,代表作如下:
- 个体学习器直接存在强依赖关系,必须串行生成的序列化方法:Boosting
- 个体学习器间不存在强依赖关系,可以同时生成的并行化方法:Bagging 和 随机森林 (Random Forest)
8.2 Boosting
Boosting 算法族的逻辑:
- 个体学习器之间存在强依赖关系
- 串行生成每一个个体学习器
- 每生成一个新的个体学习器都要调整样本分布
以 AdaBoost 算法为例,问题式逐步深入算法实现:
如何计算最终集成的结果?利用加性模型 (additive model),假定第
i i h ( x ) h(x) i i α i \alpha_i H ( x ) H(x) H ( x ) = sign ( ∑ i = 1 T α i h i ( x ) ) H(x) = \text{sign} \left(\sum_{i=1}^T \alpha_i h_i(x)\right) 如何确定每一个学习器的权重
α i \alpha_i α i = 1 2 ln ( 1 − ϵ i ϵ i ) \displaystyle \alpha_i=\frac{1}{2}\ln (\frac{1-\epsilon_i}{\epsilon_i}) 如何调整样本分布?我们对样本进行赋权。学习第一个学习器时,所有的样本权重相等,后续学习时的样本权重变化规则取决于上一个学习器的分类情况。上一个分类正确的样本权重减小,上一个分类错误的样本权重增加,即:
D i + 1 ( x ) = D i ( x ) Z i × { e − α i , h i ( x ) = f ( x ) e α i , h i ( x ) ≠ f ( x ) D_{i+1}(x) = \frac{D_i(x)}{Z_i} \times \begin{cases}e^{-\alpha_i}&,h_i(x)=f(x) \\e^{\alpha_i}&,h_i(x)\ne f(x)\end{cases}
代表算法:AdaBoost、GBDT、XGBoost
8.3 Bagging 与 随机森林
在指定学习器个数
8.3.1 Bagging
问题式逐步深入 Bagging 算法实现:
- 如何计算最终集成的结果?直接进行大数投票即可,注意每一个学习器都是等权重的
- 如何选择每一个训练器的训练样本?顾名思义,就是进行
T T - 如何选择基学习器?往往采用决策树 or 神经网络
8.3.2 随机森林
问题式逐步深入随机森林 (Random Forest,简称 RF) 算法实现:
- 如何计算最终集成的结果?直接进行大数投票即可,注意每一个学习器都是等权重的
- 为什么叫森林?每一个基学习器都是「单层」决策树
- 随机在哪?首先每一个学习器对应的训练样本都是随机的,其次每一个基学习器的属性都是随机的
k ( k ∈ [ 1 , V ] ) k(k \in [1,V])
8.3.3 区别与联系(补)
区别:随机森林与 Bagging 相比,多增加了一个属性随机,进而提升了不同学习器之间的差异度,进而提升了模型性能,效果如下:
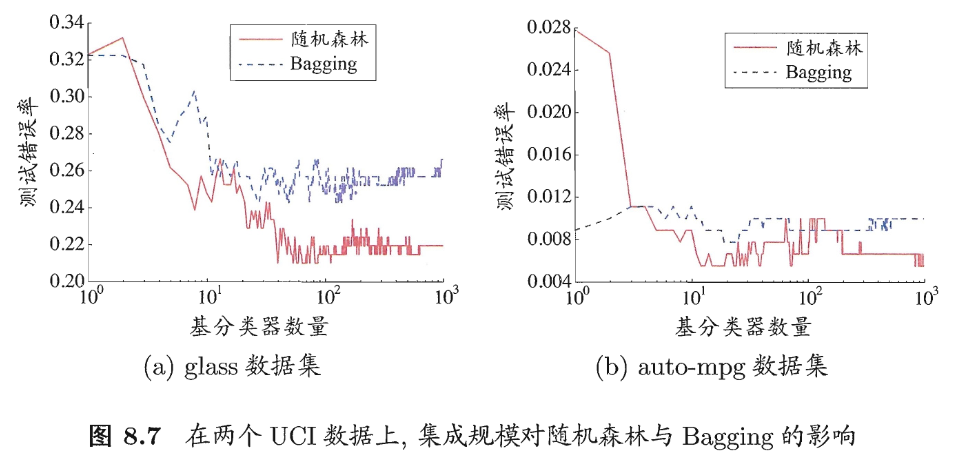
联系:两者均采用自助采样法。优势在于,不仅解决了训练样本不足的问题,同时 T 个学习器的训练样本之间是有交集的,这也就可以减小测试的方差。
8.4 区别与联系(补)
区别:
- 序列化基学习器最终的集成结果往往采用加权投票
- 并行化基学习器最终的集成结果往往采用平权投票
联系:
- 序列化减小偏差。即可以增加拟合性,降低欠拟合
- 并行化减小方差。即可以减少数据扰动带来的误差
8.5 结合策略
基学习器有了,如何确定最终模型的集成输出呢?我们假设每一个基学习器对于当前样本
8.5.1 平均法
对于数值型输出
- 简单平均法:
H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(x) = \displaystyle \frac{1}{T} \sum_{i =1}^T h_i(x) - 加权平均法:
H ( x ) = ∑ i = 1 T w i h i ( x ) , w i ≥ 0 , ∑ i = 1 T w i = 1 H(x) = \displaystyle\sum_{i=1}^T w_i h_i(x),\quad w_i \ge 0, \sum_{i=1}^Tw_i = 1
显然简单平均法是加权平均法的特殊。一般而言,当个体学习器性能差距较大时采用加权平均法,相近时采用简单平均法。
8.5.2 投票法
对于分类型输出
- 绝对多数投票法:选择超过半数的,如果没有则拒绝投票
- 相对多数投票法:选择票数最多的,如果有多个相同票数的则随机取一个
- 加权投票法:每一个基学习器有一个权重,从而进行投票
8.5.3 学习法
其实就是将所有基学习器的输出作为训练数据,重新训练一个模型对输出结果进行预测。其中,基学习器称为“初级学习器”,输出映射学习器称为“次级学习器”或”元学习器”
其中
- Stacking
- 多响应线性回归
(Mutil-response linear regression, 简称 MLR) \text{(Mutil-response linear regression, 简称 MLR)} - 贝叶斯模型平均
(Bayes Model Averaging, 简称 BMA) \text{(Bayes Model Averaging, 简称 BMA)}
经过验证,Stacking 的泛化能力往往比 BMA 更优。
8.6 多样性
8.6.1 误差-分歧分解
根据「回归」任务的推导可得下式。其中
8.6.2 多样性度量
如何估算个体学习器的多样化程度呢?典型做法是考虑两两学习器的相似性。所有指标都是从两个学习器的分类结果展开,以两个学习器

显然
- 不合度量
- 相关系数
- Q-统计量
κ \kappa
以「
- 串行的基学习器多样性较并行的基学习器更高
- 串行的基学习器误差较并行的基学习器也更高

8.6.3 多样性增强
为了训练出多样性大的个体学习器,我们引入随机性。介绍几种扰动策略:
- 数据样本扰动
- 输入属性扰动
- 输出表示扰动
- 算法参数扰动
第9章 聚类
9.1 聚类任务
典型的无监督学习方法。即将众多无标签数据进行分类。在开始介绍几类经典的聚类学习方法之前,我们先讨论聚类算法涉及到的两个基本问题:性能度量和距离计算。
9.2 性能度量
一来是进行聚类的评估,二来也可以作为聚类的优化目标。分为两种,分别是外部指标和内部指标。
9.2.1 外部指标
所谓外部指标就是已经有一个“参考模型”存在了,将当前模型与参考模型的比对结果作为指标。我们考虑两两样本的聚类结果,定义下面的变量:
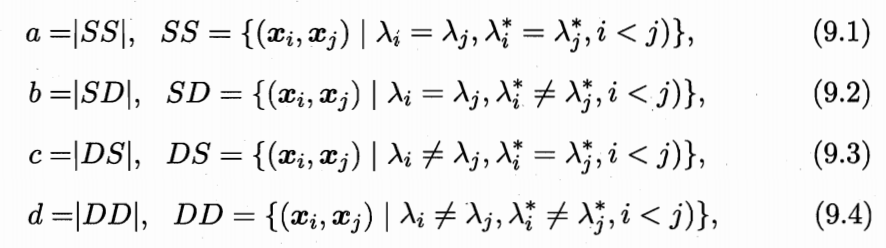
显然
- JC 指数:
J C = a a + b + c \displaystyle JC = \frac{a}{a+b+c} - FM 指数:
a a + b ⋅ a a + c \displaystyle \sqrt{\frac{a}{a+b} \cdot \frac{a}{a+c}} - RI 指数:
2 ( a + d ) m ( m − 1 ) \displaystyle \frac{2(a+d)}{m(m-1)}
上述指数取值均在
9.2.2 内部指标
所谓内部指标就是仅仅考虑当前模型的聚类结果。同样考虑两两样本的聚类结果,定义下面的变量:
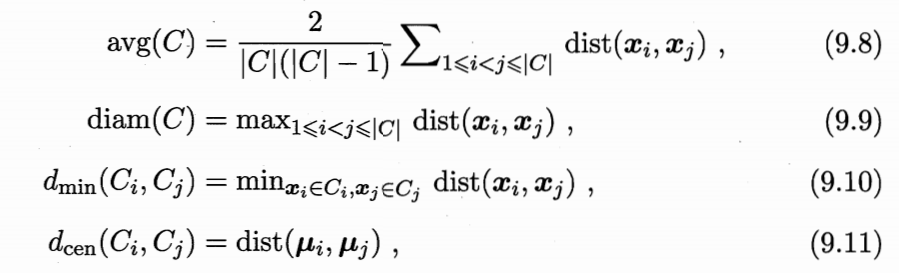
常见的外部指标如下:
- DB 指数
- Dunn 指数
9.3 距离计算
有序属性:闵可夫斯基距离
无序属性:VDM 距离
9.4 原型聚类
9.4.1 k 均值算法
算法流程大体上可以归纳为三步:
- 初始化 k 个聚类中心
- 枚举所有样本并将其划分到欧氏距离最近的中心
- 更新 k 个簇中心
重复上述迭代过程直到聚类中心不再发生变化,当然为了防止迭代时间过久,可以弱化迭代终止条件,比如增设:最大迭代论述或对聚类中心的变化增加一个阈值而非绝对的零变化。k 均值算法伪代码如下:

9.4.2 学习向量量化算法
9.4.3 高斯混合聚类算法

9.5 密度聚类
DBSCAN 算法
适用于簇的大小不定,距离不定的情况。大概就是多源有向bfs的过程。定义每一源为“核心对象”,每次以核心对象为起始进行bfs,将每一个符合“范围约束”的近邻点纳入当前簇,不断寻找知道所有核心对象都访问过为止。
9.6 层次聚类
AGNES 算法
适用于可选簇大小、可选簇数量的情况。
第10章 降维与度量学习
本章我们通过 k 近邻监督学习方法引入「降维」和「度量学习」的概念。
- 对于降维算法:根本原因是样本往往十分稀疏,需要我们对样本的属性进行降维,从而达到合适的密度进而可以进行基于距离的邻居选择相关算法。我们将重点讨论以下几个降维算法:MDS 多维缩放、PCA 主成分分析、等度量映射
- 对于度量学习:上述降维的根本目的是选择合适的维度,确保一定可以通过某个距离计算表达式计算得到每一个样本的 k 个邻居。而度量学习直接从目的出发,尝试直接学习样本之间的距离计算公式。我们将重点讨论以下几个度量学习算法:近邻成分分析、LMNN
10.1 k 近邻学习
k 近邻(k-Nearest Neighbor,简称 KNN)是一种监督学习方法。一句话概括就是「近朱者赤近墨者黑」,每一个测试样本的分类或回归结果取决于在某种距离度量下的最近的 k 个邻居的性质。不需要训练,可以根据检测样本实时预测,即懒惰学习。为了实现上述监督学习的效果,我们需要解决以下两个问题:
- 如何确定「距离度量」的准则?就那么几种,一个一个试即可。
- 如何定义「分类结果」的标签?分类任务是 k 个邻居中最多类别的标签,回归任务是 k 个邻居中最多类别标签的均值。
上述学习方法有什么问题呢?对于每一个测试样例,我们需要确保能够通过合适的距离度量准则选择出 k 个邻居出来,这就需要保证数据集足够大。在距离计算时,每一个属性都需要考虑,于是所需的样本空间会呈指数级别的增长,这被称为「维数灾难」。这是几乎不可能获得的数据量同时在进行矩阵运算时时间的开销也是巨大的。由此引入本章的关键内容之一:降维。
为什么能降维?我们假设学习任务仅仅是高维空间的一个低维嵌入。
10.2 多维缩放降维
「多维缩放(MDS)降维算法」的原则:对于任意的两个样本,降维后两个样本之间的距离保持不变。
基于此思想,可以得到以下降维流程:我们定义
内积计算:

新属性值计算:特征值分解法。其中

10.3 主成分分析降维
「主成分分析(Principal Component Analysis,简称 PCA)降维算法」的两个原则:
- 样本到超平面的距离都尽可能近
- 样本在超平面的投影都尽可能分开
基于此思想可以得到 PCA 的算法流程:

假设我们有一个简单的数据集
我们希望将这些样本从二维空间降维到一维空间(即
步骤 1: 样本中心化
首先计算样本的均值向量:
然后对所有样本进行中心化:
步骤 2: 计算协方差矩阵
样本的协方差矩阵为:
步骤 3: 对协方差矩阵进行特征值分解
协方差矩阵的特征值分解:
特征值为
步骤 4: 取最大的
我们选择最大的特征值对应的特征向量
10.4 核化线性降维
「核化线性降维算法」的原则:pass
10.5 流形学习降维
假定数据满足流形结构。
10.5.1 等度量映射
流形样本中,直接计算两个样本之间的欧式距离是无效的。我们引入「等度量映射」理念。根本算法逻辑是:利用最短路算法计算任意两个样本之间的「测地线距离」得到
10.5.2 局部线性嵌入
pass
10.6 度量学习
降维的本质是寻找一种合适的距离度量方法,与其降维为什么不直接学习一种距离计算方法呢?我们引入「度量学习」的理念。
为了“有参可学”,我们需要定义距离计算表达式中的超参,我们定义如下「马氏距离」:
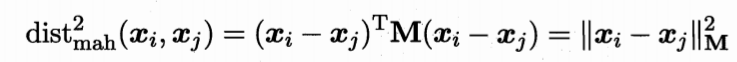
为什么用所谓的马氏距离呢?欧氏距离不行吗?我们有以下结论:
- 欧式距离具有旋转不变性和平移不变性,在低维和属性直接相互独立时是最佳实践。但是当属性之间有相关性并且尺度相差较大时,直接用欧式距离计算会丢失重要的特征之间的信息;
- 马氏距离具有尺度不变性,在高维和属性之间有关系且尺度不同时是最佳实践。缺点在于需要计算协方差矩阵导致计算量远大于欧氏距离的计算量。
下面介绍两种度量学习算法来学习上述 M 矩阵,也就是数据集的「协方差矩阵的逆」中的参数。准确的说是学习一个矩阵来近似代替协方差矩阵的逆矩阵。
10.6.1 近邻成分分析
近邻成分分析
10.6.2 LMNN
大间隔最近邻
paper: Distance Metric Learning for Large Margin Nearest Neighbor Classification
explain: 【LMNN】浅析"从距离测量到基于Margin的邻近分类问题"
第13章 半监督学习
半监督学习的根本目标:同时利用有标记和未标记样本的数据进行学习,提升模型泛化能力。主要分为三种:
- 主动学习
- 纯半监督学习
- 直推学习
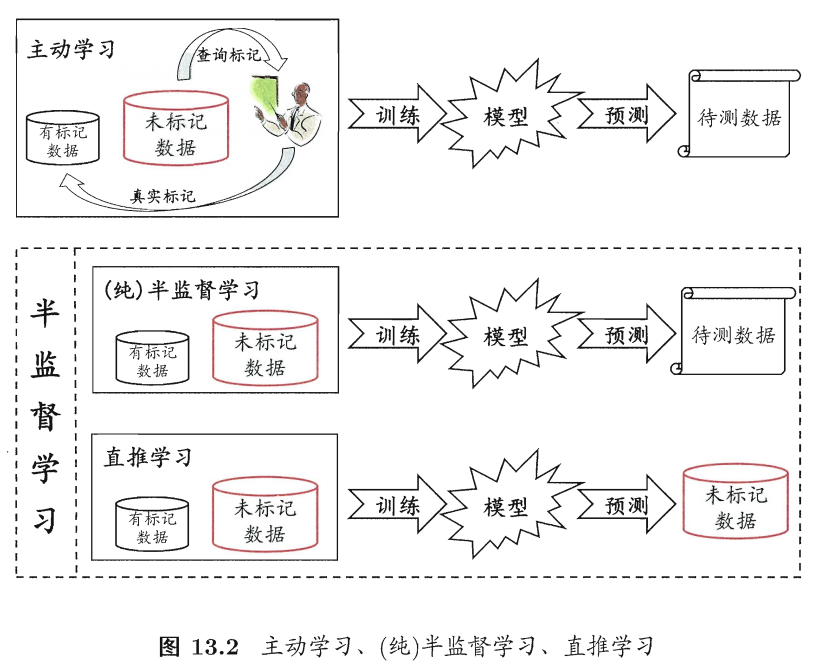
13.1 未标记样本
对未标记数据的分布进行假设,两种假设:
- 簇状分布
- 流形分布
13.2 生成式方法
分别介绍「生成式方法」和「判别式方法」及其区别和联系。
生成式方法:核心思想就是用联合分布
- 朴素贝叶斯
- 高斯混合聚类
- 马尔科夫模型
判别式方法:核心思想就是用条件分布
- 线性回归
- 逻辑回归
- 决策树
- 神经网络
- 支持向量机
- 条件随机场
自监督训练(补)
根本思想就是利用有标记数据进行模型训练,然后对未标记数据进行预测,选择置信度较高的一些样本加入训练集重新训练模型,不断迭代进行直到最终训练出来一个利用大量未标记数据训练出来的模型。
如何定义置信度高?我们利用信息熵的概念,即对于每一个测试样本都有一个预测向量,信息熵越大表明模型对其的预测结果越模糊,因此置信度高正比于信息熵小,将信息熵较小的测试样本打上「伪标记」加入训练集。
13.3 半监督 SVM
以经典 S3VM 中的经典算法 TSVM 为例。给出优化函数、算法图例、算法伪代码:
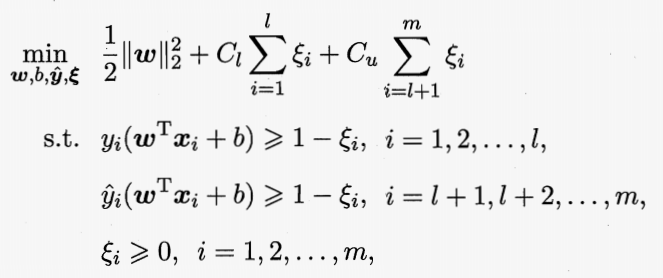


13.4 图半监督学习
同样解决分类问题,以「迭代式标记传播算法」为例。
二分类,可以直接求出闭式解。
算法逻辑。每一个样本对应图中的一个结点,两个结点会连上一个边,边权正比于两结点样本的相似性。最终根据图中已知的某些结点进行传播标记即可。与基于密度的聚类算法类似,区别在于此处不同的簇 cluster 可能会对应同一个类别 class。
如何进行连边?不会计算每一个样本的所有近邻,一般采用局部近邻选择连边的点,可以 k 近邻,也可以范围近邻。
优化函数。定义图矩阵的能量损失函数为图中每一个结点与所有结点的能量损失和,目标就是最小化能量损失和:
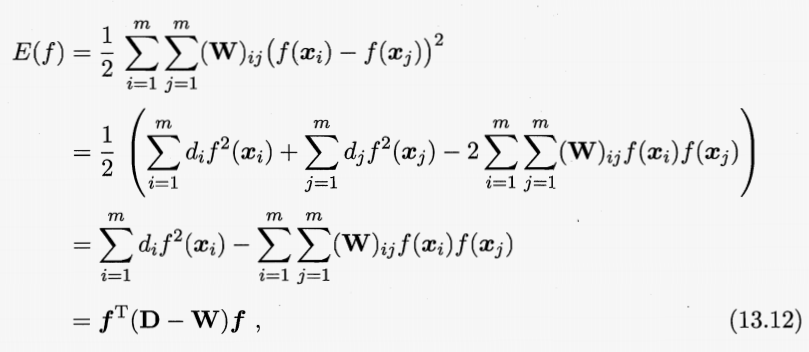
多分类,无法直接求出闭式解,只能进行迭代式计算。
新增变量。我们定义标记矩阵 F,其形状为

13.5 基于分歧的方法
多学习器协同训练。
第14章 概率图模型
为了分析变量之间的关系,我们建立概率图模型。按照图中边的性质可将概率图模型分为两类:
- 有向图模型,也称贝叶斯网
- 无向图模型,也称马尔可夫网
14.1 隐马尔可夫模型
隐马尔可夫模型
需要解决三个问题:
- 如何评估建立的网络模型和实际观测数据的匹配程度?
- 如果上面第一个问题中匹配程度不好,如何调整模型参数来提升模型和实际观测数据的匹配程度呢?
- 如何根据实际的观测数据利用网络推断出有价值的隐藏状态?
14.2 马尔科夫随机场
马尔科夫随机场
联合概率计算逻辑按照势函数和团展开。其中团可以理解为完全子图;极大团就是结点最多的完全子图,即在当前的完全子图中继续添加子图之外的点就无法构成新的完全子图;势函数就是一个关于团的函数。
14.3 条件随机场
判别式方法。
14.4 学习和推断
精确推断。
14.5 近似推断
近似推断。降低计算时间开销。
- 采样法:蒙特卡洛采样法
- 变分推断:考虑近似分布
考试大纲
- 单选
10 * 3':单选直接一个单刀咆哮。注意审题、注意一些绝对性的语句; - 简答
4 * 5':想拿满分就需要写出理论对应的具体公式; - 计算
3 * 10':老老实实写每一个计算过程,不要跳步骤; - 论述
2 * 10':没考过,大约是简答题加强版。注意逻辑一定要清晰。
前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 杨琬琪 | 3 | 专业课 |
成绩组成:
理论课:
| 作业+课堂 | 课堂测验(2次) | 期末(闭卷) |
|---|---|---|
| 30% | 20% | 50% |
实验课:
| 19次实验(五级制) |
|---|
| 100% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 机器学习与模式识别 | 《机器学习与模式识别》 | – | 周志华 | 清华大学出版社 | 978-7-302-42328-7 |
学习资源:
- 🍉 西瓜书 📺 视频、PPT 资源:机器学习初步、PPT - 百度网盘链接
- 🍉 西瓜书 📖 电子资源:Machine_Learning/机器学习_周志华.pdf
- 🎃 南瓜书 📺 视频资源:《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
- 🎃 南瓜书 📖 电子资源:《机器学习》(西瓜书)公式详解
实验平台:
- AI Studio:https://aistudio.baidu.com/index
本地路径:
- 🍉 西瓜书电子书:[机器学习_周志华](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_周志华.pdf)
- 🎃 南瓜书电子书:[pumpkin_book](D:\华为云盘\2. Score\4. 机器学习与模式识别\pumpkin-book\pdf\pumpkin_book_1.9.9.pdf)
- 📃 上课 PPT by 周志华:[机器学习_课件_周志华](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_课件_周志华)
- 📃 上课 PPT by 杨琬琪:[机器学习_课件_杨琬琪](D:\华为云盘\2. Score\4. 机器学习与模式识别\机器学习_课件_杨琬琪)
第1章 绪论
1.1 引言
pass
1.2 基本术语
| Name | Introduction |
|---|---|
| 机器学习定义 | 利用经验改善系统自身性能,主要研究智能数据分析的理论和方法。 |
| 计算学习理论 | 最重要的理论模型是 PAC(Probably Approximately Correct, 概率近似正确) learning model,即以很高的概率得到很好的模型 $P( |
| P 问题 | 在多项式时间内计算出答案的解 |
| NP 问题 | 在多项式时间内检验解的正确性 |
| 特征(属性) | – |
| 特征(属性)值 | 连续 or 离散 |
| 样本维度 | 特征(属性)个数 |
| 特征(属性、输入)空间 | 特征张成的空间 |
| 标记(输出)空间 | 标记张成的空间 |
| 样本 | <x> |
| 样例 | <x,y> |
| 预测任务 | 监督学习、无监督学习、半监督学习、噪音标记学习、多标记学习 |
| 泛化能力 | 应对未来未见的测试样本的能力 |
| 独立同分布假设 | 历史和未来的数据来自相同的分布 |
1.3 假设空间
假设空间:所有可能的样本组合构成的集合空间
版本空间:根据已知的训练集,将假设空间中与正例不同的、反例一致的样本全部删掉,剩下的样本组合构成的集合空间
1.4 归纳偏好
No Free Launch 理论,没有很好的算法,只有适合的算法。好的算法来自于对数据的好假设、好偏执,大胆假设,小心求证
1.5 发展历程
pass
1.6 应用现状
pass
第2章 模型评估与选择
2.1 经验误差与过拟合
概念辨析
- 错误率:针对测试数据而言,分错的样本数
a a m m E = a m E=\frac{a}{m} - 经验误差:针对训练数据而言,随着训练轮数或模型的复杂度越高,经验误差越小

过拟合解决方法
Early Stopping (当发现有过拟合现象就停止训练)
Penalizing Large Weight (在经验风险上加一个正则化项)
▶正则化概念补充在后面的学习中经常会和正则化打交道,因此此处补充一下相关的概念。
在目标函数中添加正则化到底有什么好处?给几个解释:
- 防止过拟合。为什么可以防止过拟合?其实可以形象化的将添加的正则化项理解为一个可以调节的「累赘」,为了让原始问题尽可能的最优,我让累赘愈发拖累目标函数的取值,这样原始问题就不得不更优以此来抵消累赘带来的拖累。
- 可以进行特征选择。个人认为属于第一点的衍生意义,为什么这么说?同样用累赘来比喻正则化项。当原始问题的某些变量为了代偿拖累导致系数都接近于零了,那么这个变量也就没有存在的意义了,于是对应的特征也就被筛选掉了,也就是所谓的特征选择了。常常添加 L1 正则化项来进行所谓的特征选择。
- 提升计算效率。同样可以理解为第三点的衍生意义,为什么这么说?因为你都把变量筛掉了,那么对应的解空间是不是就相应的大幅度减少了,于是最优解的搜索也就更加快速了。
当然正则化项并非万能的万金油,在整个目标函数中正则化项有这举足轻重的意义,一旦正则化项的系数发生了微小的变动,对于整个模型的影响都是巨大的。因此有时添加正则化项并不一定可以带来泛化性能的提升。
正则化有以下形式:
一般式:
∣ ∣ x ∣ ∣ p k = ( ( ∑ i = 1 m ∣ x i ∣ p ) 1 p ) k ||\mathbf{x}||_p^k = \left ( \left ( \sum_{i=1}^{m}|x_i|^{p} \right)^{\frac{1}{p}} \right)^k L1 正则化:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 m ∣ x i ∣ ||\mathbf{x}||_1 = \sum_{i=1}^m |x_i| L2 正则化:
∣ ∣ x ∣ ∣ 2 2 = ( ( ∑ i = 1 m ∣ x i ∣ 2 ) 1 2 ) 2 = ∑ i = 1 m ∣ x i ∣ 2 \begin{aligned}||\mathbf{x}||_2^2 &= \left ( \left ( \sum_{i=1}^{m}|x_i|^{2} \right)^{\frac{1}{2}} \right)^2 \\&= \sum_{i=1}^{m}|x_i|^{2}\end{aligned}
Bagging 思想 (对同一样本用多个模型投票产生结果)
Boosting 思想 (多个弱分类器增强分类能力,降低偏差)
Dropconnection (神经网络全连接层中减少过拟合的发生)
欠拟合解决方法
决策树:拓展分支
神经网络:增加训练轮数
2.2 评估方法
留出法(hold-out):将数据集分为三个部分,分别为训练集、验证集、测试集。测试集对于训练是完全未知的,我们划分出测试集是为了模拟未来未知的数据,因此当下的任务就是利用训练集和验证集训练出合理的模型来尽可能好的拟合测试集。那么如何使用划分出的训练集和验证集来训练、评估模型呢?就是根据模型的复杂度 or 模型训练的轮数,根据上图的曲线情况来选择模型。
交叉验证法(cross validation):一般方法为 p 次 k 折交叉验证,即 p 次将训练数据随机划分为 k 个大小相似的互斥子集。将其中
k − 1 k-1 1 1 k k 自助法(bootstrapping):有放回采样获得训练集。每轮从数据集
D D m m m m m m D ′ D' 2 3 \frac{2}{3} D ′ D' D − D ′ D-D' ▶测试集占比 1/3 证明过程
2.3 性能度量
2.3.1 回归任务
均方误差:
均方根误差:
首先理解各部分的含义。减数的分子表示预测数据的平方差,减数的分母表示真实数据的平方差。而平方差是用来描述数据离散程度的统计量。
为了保证回归拟合的结果尽可能不受数据离散性的影响,我们通过相除来判断预测的数据是否离散。如果和原始数据离散性差不多,那么商就接近1,R方就接近0,表示性能较差,反之如果比原始数据离散性小,那么商就接近0,R方就接近1,表示性能较优。
2.3.2 分类任务
混淆矩阵

准确率(accuracy):
P = T P + T N T P + F N + F P + T N \displaystyle P=\frac{TP+TN}{TP+FN+FP+TN} 查准率/精度(precision):
P = T P T P + F P \displaystyle P = \frac{TP}{TP+FP} 查全率/召回率(recall):
R = T P T P + F N \displaystyle R = \frac{TP}{TP+FN} F1 度量(F1-score):
F 1 = 2 × P × R P + R \displaystyle F_1 = \frac{2\times P \times R}{P + R} 对于多分类问题,我们可以将该问题分解为多个二分类问题(ps:假设为 n 个)。从而可以获得多个上述的混淆矩阵,那么也就获得了多个
P i P_i R i R_i T P ‾ \overline{TP} F P ‾ \overline{FP} F N ‾ \overline{FN} 宏
- 宏查准率:
m a c r o P = 1 n ∑ i = 1 n P i \displaystyle macroP = \frac{1}{n} \sum_{i=1}^n P_i - 宏查全率:
m a c r o R = 1 n ∑ i = 1 n R i \displaystyle macroR = \frac{1}{n} \sum_{i=1}^n R_i - 宏
F 1 F1 m a c r o F 1 = 2 × m a c r o P × m a c r o R m a c r o P + m a c r o R \displaystyle macroF_1 = \frac{2 \times macroP \times macroR}{macroP+macroR}
- 宏查准率:
微
- 微查准率:
m i c r o P = T P ‾ T P ‾ + F P ‾ \displaystyle microP = \frac{\overline{TP}}{\overline{TP}+\overline{FP}} - 微查全率:
m i c r o R = T P ‾ T P ‾ + F N ‾ \displaystyle microR = \frac{\overline{TP}}{\overline{TP}+\overline{FN}} - 微
F 1 F1 m i c r o F 1 = 2 × m i c r o P × m i c r o R m i c r o P + m i c r o R \displaystyle microF_1 = \frac{2 \times microP \times microR}{microP+microR}
- 微查准率:
P-R 曲线

横纵坐标:横坐标为查全率(Recall),纵坐标为查准率(Precision)
如何产生?我们根据学习器对于每一个样本的预测值(正例性的概率)进行降序排序,然后调整截断点将预测后的样本进行二分类,将截断点之前的所有数据全部认为预测正例,截断点之后的所有数据全部认为预测反例。然后计算两个指标进行绘图。
▶什么分类任务中的是预测值?我们知道学习器得到最终的结果一般不是一个绝对的二值,如 0,1。往往是一个连续的值,比如 [0,1],也就是“正例性的概率”。因此我们才可以选择合适的截断点将所有的样本数据划分为两类。
趋势解读:随着截断点的值不断下降,很显然查全率
R R P P 不同曲线对应学习器的性能度量:曲线与横纵坐标围成的面积衡量了样本预测排序的质量。因此上图中 A 曲线的预测质量比 C 曲线的预测质量高。但是我们往往会遇到比较 A 与 B 的预测质量的情况,由于曲线与坐标轴围成的面积难以计算,因此我们引入了平衡点的概念。平衡点就是查准率与查询率相等的曲线,即
P = R P=R
ROC 曲线与 AUC ⭐

横纵坐标:横坐标为假正例率
F P R = F P F P + T N \displaystyle FPR = \frac{FP}{FP+TN} T P R = T P T P + F N \displaystyle TPR = \frac{TP}{TP+FN} 如何产生?与 P-R 图的产生类似,只不过计算横纵坐标的规则不同,不再赘述。
趋势解读:随着截断点的值不断下降,真正例率与假正例率均会不断上升,因为分子都是从 0 开始逐渐增加的
不同曲线对应学习器的性能度量:AUC 衡量了样本预测的排序质量。AUC 即 ROC 曲线右下方的面积,面积越大则对应的预测质量更高,学习器性能更好。不同于上述引入平衡点的概念,此处的面积我们可以直接计算,甚至 1-AUC 也可以直接计算。
我们定义
AUC \text{AUC} ∑ i = 1 m − 1 ( y i + y i + 1 ) ⋅ ( x i + 1 − x i ) 2 \sum _{i=1}^{m-1} \frac{(y_{i}+y_{i+1}) \cdot (x_{i+1} - x_i)}{2} 我们定义损失函数(
l o s s loss l r a n k = 1 − A U C l_{rank} = 1-AUC 
2.4 比较检验
理论依据:统计假设检验(hypothesis test)
两个学习器性能比较:
交叉验证 t 检验:对于 k 折两个学习期产生的 k 个误差之差,求得其均值
μ \mu σ 2 \sigma ^2 Γ t \Gamma_t Γ t \Gamma_t Γ t = ∣ k μ σ ∣ \Gamma_t = |\frac{\sqrt{k}\mu}{\sigma}| McNemar 检验:对于二分类问题,我们可以得到下方的列联表

若变量
Γ χ 2 \Gamma_{\chi ^2} Γ χ 2 \Gamma_{\chi ^2} Γ χ 2 = ( ∣ e 01 − e 10 ∣ − 1 ) 2 e 01 + e 10 \Gamma_{\chi ^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01}+e_{10}}
2.5 偏差与方差
现在我们得到了学习算法的泛化性能,我们还想知道为什么会有这样的泛化性能,即我们应该如何理论的解释这样的泛化性能呢?我们引入 偏差-方差分解 的概念来从理论的角度解释期望泛化误差。那么这个方法一定是完美解释的吗?也有一定的缺点,因此我们还会引入 偏差-方差窘境 的概念来解释偏差和方差对于泛化误差的贡献。
在此之前我们需要知道偏差、方差和噪声的基本定义:
- 偏差:学习算法的期望输出与真实结果的偏离程度,刻画算法本身的拟合能力。
- 方差:使用同规模的不同训练集进行训练时带来的性能变化,刻画数据扰动带来的影响。
- 噪声:当前任务上任何算法所能达到的期望泛化误差的下界(即不可能有算法取得更小的误差),刻画问题本身的难度。
2.5.1 偏差-方差分解
我们定义以下符号:
我们以回归任务为例:(下面的全部变量均为在所有相同规模的训练集下得到的期望结果)
- 输出:
f ‾ ( x ) = E D [ f ( x ; D ) ] \overline{f}(x) = E_D[f(x;D)] - 方差:
v a r ( x ) = E D [ ( f ‾ ( x ) − f ( x ; D ) ) 2 ] var(x) = E_D[(\overline{f}(x) - f(x;D))^2] - 偏差:
b i a s 2 ( x ) = ( f ‾ ( x ) − y ) 2 bias^2(x) = (\overline{f}(x) - y)^2 - 噪声:
ϵ 2 = E D [ ( y D − y ) 2 ] \epsilon ^2 = E_D[(y_D - y)^2]
偏差-方差分解的结论:
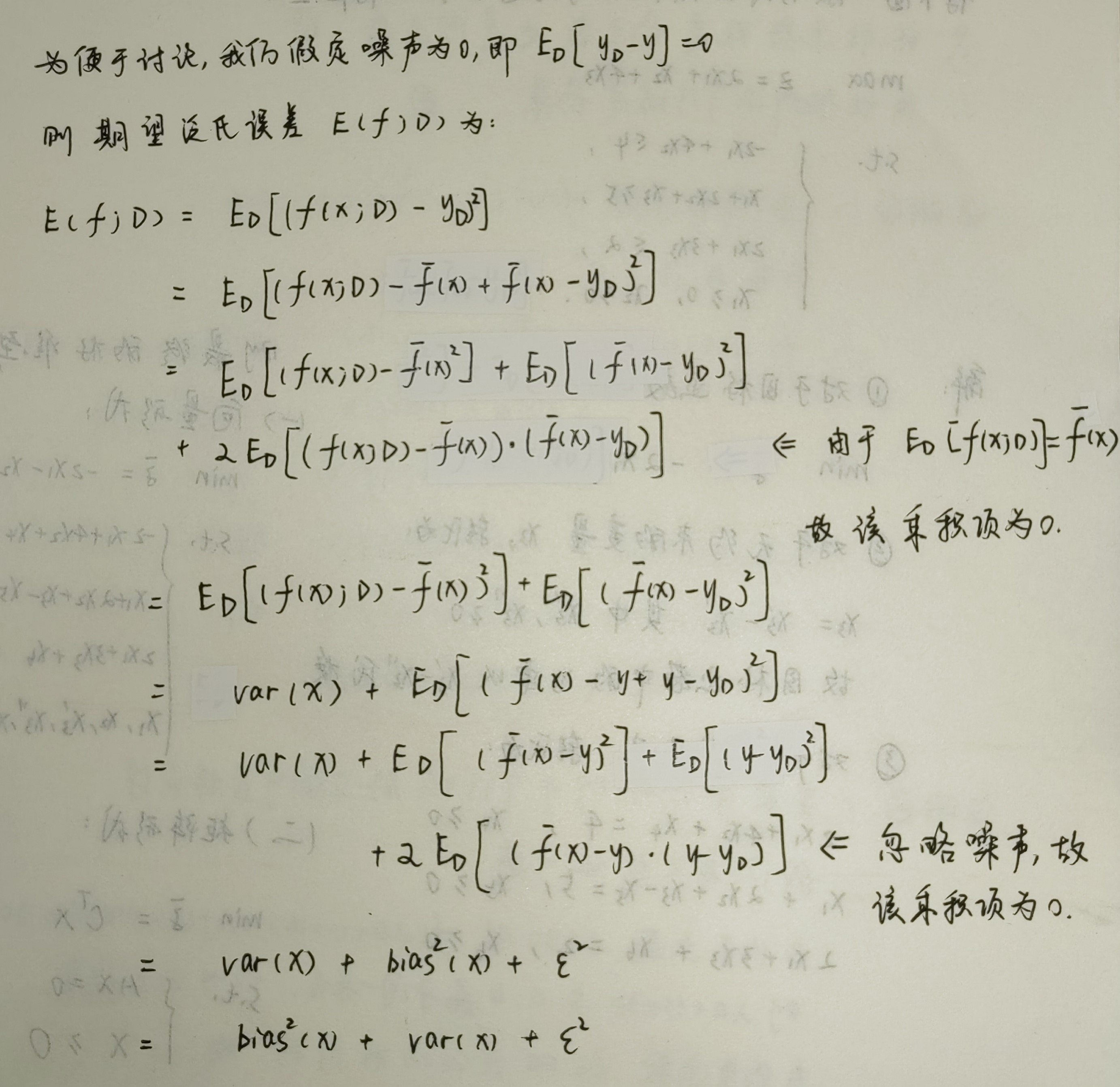
解释说明:泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定的。因此给定一个学习任务,我们可以从偏差和方差两个角度入手进行优化,即需要使偏差较小(充分拟合数据),且需要使方差较小(使数据扰动产生的影响小)
2.5.2 偏差-方差窘境
其实偏差和方差是有冲突的,这被称为偏差-方差窘境(bias-variance-dilemma)。对于以下的示意图我们可以知道:对于给定的学习任务。一开始拟合能力较差,学习器对于不同的训练数据不够敏感,此时泛化错误率主要来自偏差;随着训练的不断进行,学习器的拟合能力逐渐增强,对于数据的扰动更加敏感,使得方差主导了泛化错误率;在训练充分以后,数据的轻微扰动都可能导致预测输出发生显著的变化,此时方差就几乎完全主导了泛化错误率。

第3章 线性模型
本章介绍机器学习模型之线性模型,将从学习任务展开。学习任务分别为:
- 回归(最小二乘法、岭回归)
- 二分类(对数几率(逻辑)回归、线性判别分析)
- 多分类(一对一、一对其余、多对多)
3.1 基本形式
线性模型的优点:形式简单、易于建模、高可解释性、非线性模型的基础
线性模型的缺点:线性不可分
3.2 线性回归
预测式已经在 3.1 中标明了,现在的问题就是,如何获得
在正式开始介绍求解参数
基于均方误差最小化的模型求解方法被称为 最小二乘法 (least squre method)。而求解
于是问题就转化为了无约束的最优化问题求解。接下来我们将从一元线性回归引入,进而推广到多维线性回归的参数求解,最后补充广义的线性回归与其他线性回归的例子。
3.2.1 一元线性回归
现在假设只有一个属性 x,对应一维输出 y。现在我们试图根据已知的 <x,y> 样本数据学习出一个模型
前置说明:在机器学习中,很少有闭式解(解析解),但是线性回归是特例,可以解出闭式解。
闭式解推导过程:
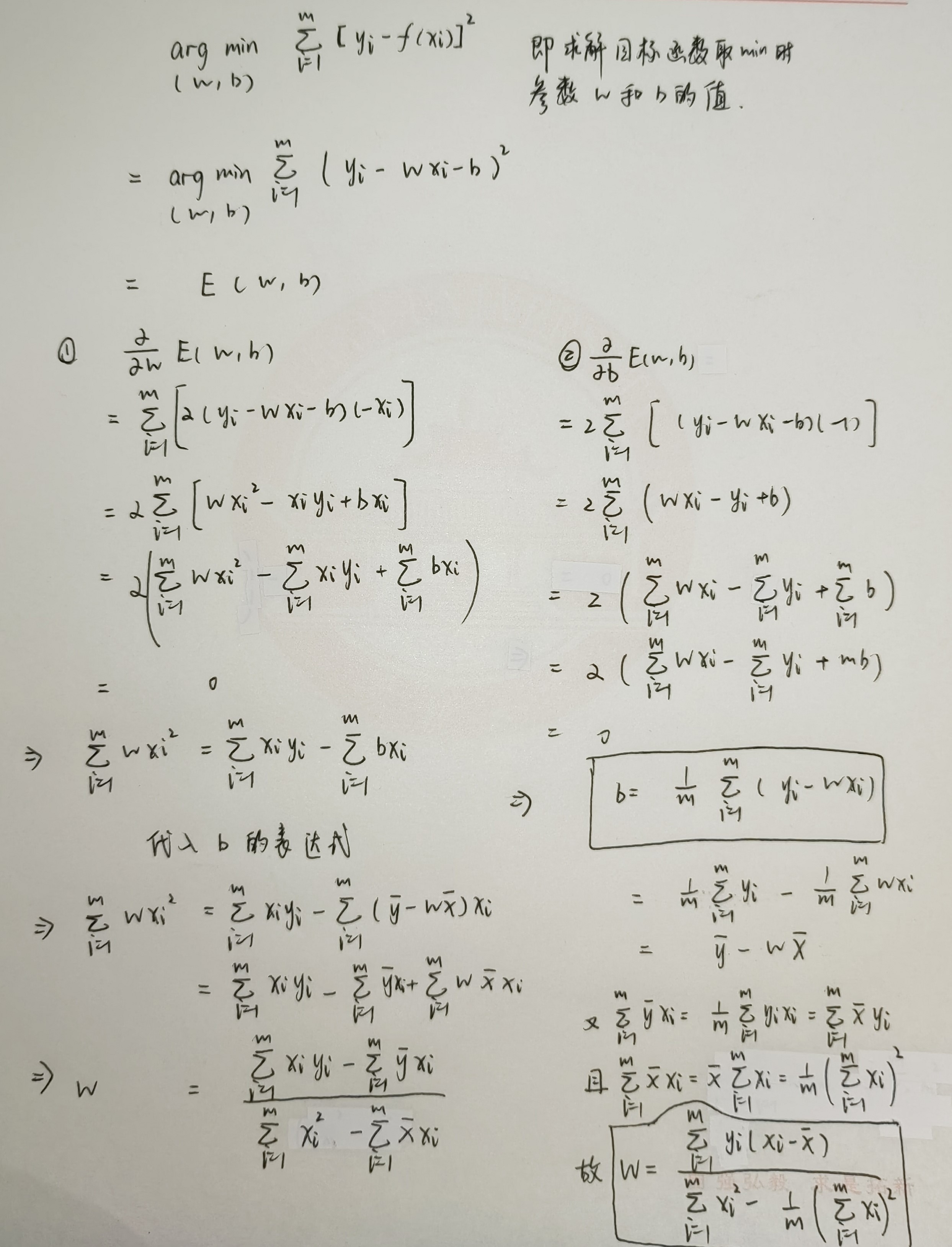
3.2.2 多元线性回归
现在我们保持输出不变,即
现在我们按照原来的方法进行求解。在求解之前我们采用向量的方式简化一下数据的表示,
于是损失函数
我们用同样的方法求解其闭式解:

我们不能直接等式两边同
X T X X^T X w ^ ∗ = ( X T X ) − 1 X T y \hat w ^* = (X^TX)^{-1}X^Ty x ^ i = ( x i , 1 ) \hat x_i = (x_i,1) f ( x i ) = x ^ i T w ^ ∗ f(x_i) = \hat x_i ^T \hat w^* X T X X^T X L 2 L_2 α ∣ ∣ w ^ ∣ ∣ 2 \alpha || \hat w ||^2 现在的损失函数就定义为:
E w ^ = ( y − X w ^ ) T ( y − X w ^ ) + α ∣ ∣ w ^ ∣ ∣ 2 E_{\hat w} = (y - X \hat w) ^T (y - X \hat w) + \alpha || \hat w ||^2 同样将损失函数对参数向量
w ^ \hat w ∂ E w ^ ∂ w ^ = ⋯ = 2 X T X w ^ − 2 X T y + 2 α w ^ = 2 X T ( X w ^ − y ) + 2 α w ^ \begin{aligned}\frac{\partial E_{\hat w}}{\partial \hat w} &= \cdots \\&= 2X^TX\hat w - 2 X^T y + 2 \alpha \hat w \\&= 2 X ^T(X \hat w - y) + 2 \alpha \hat w\end{aligned} 我们令其为零,得参数向量
w ^ \hat w w ^ = ( X T X + α I ) − 1 X T y \hat w = (X^T X + \alpha I)^{-1} X^T y
3.2.3 广义线性回归
可否令模型的预测值
本质上我们训练的线性模型
此时得到的线性模型

3.2.4 其他线性回归
支持向量机回归
决策树回归
随机森林回归
LASSO 回归:增加
L 1 L_1 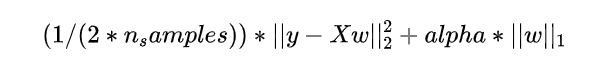
ElasticNet 回归:增加
L 1 L_1 L 2 L_2 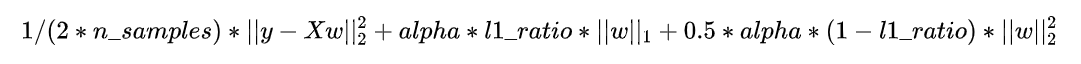
XGBoost 回归
3.3 对数几率回归
对数几率回归准确来说应该叫逻辑回归,并且不是回归的学习任务,而是二分类的学习任务。本目将从阈值函数的选择和模型参数的求解两个维度展开讲解。
3.3.1 阈值函数的选择
对于二分类任务。我们可以将线性模型的输出结果
最简单的一种阈值函数就是单位阶跃函数。映射关系如下。但是有一个问题就是单位阶跃函数不是单调可微函数,因此不可取
▶为什么阈值函数需要单调可微呢?一直有一个疑问,单位跃阶函数已经可以将线性模型的进行二值映射了,干嘛还要求阈值函数的反函数呢?
其实是因为知道的太片面了。我们的终极目的是为了通过训练数据,学习出线性模型中的
w w b b z = w T x + b z=w^Tx+b g ( ⋅ ) g(\cdot) y = g ( z ) y=g(z) w w b b E ( w , b ) = ∑ i = 1 m ( y i − g ( x i ) ) 2 E_{(w,b)} = \sum_{i=1}^m (y_i - g(x_i))^2 g ( ⋅ ) g(\cdot) 至此疑问解决!让我们畅快的学习单调可微的阈值函数吧!
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 y = \begin{cases}0, &z < 0 \\0.5,& z=0 \\1, & z>0\end{cases} 常用的一种阈值函数是对数几率函数,也叫逻辑函数(
logistic function \text{logistic function} y = 1 1 + e − z y = \frac{1}{1+e^{-z}}
3.3.2 模型参数的求解
现在我们站在前人的肩膀上学习到了一种阈值函数:逻辑函数(
这就要从逻辑函数的实际意义出发了。对于逻辑函数,我们代入线性模型,并做以下转化:
若我们定义
知道了逻辑函数的实际意义是真实标记的对数几率以后,接下来我们实际意义出发,讲解模型参数
若我们将
同时,显然有
于是我们可以确定目标函数了。我们取当前目标函数为对数似然函数:
显然的,当上述目标函数取最大值时,得到的参数
我们将变量进行一定的变形:
于是上述对数似然函数就可以进行以下转化:
进而从极大似然估计转化为:求解「极小化负的上述目标函数时」参数
由于上式是关于
目标函数:
第
其中
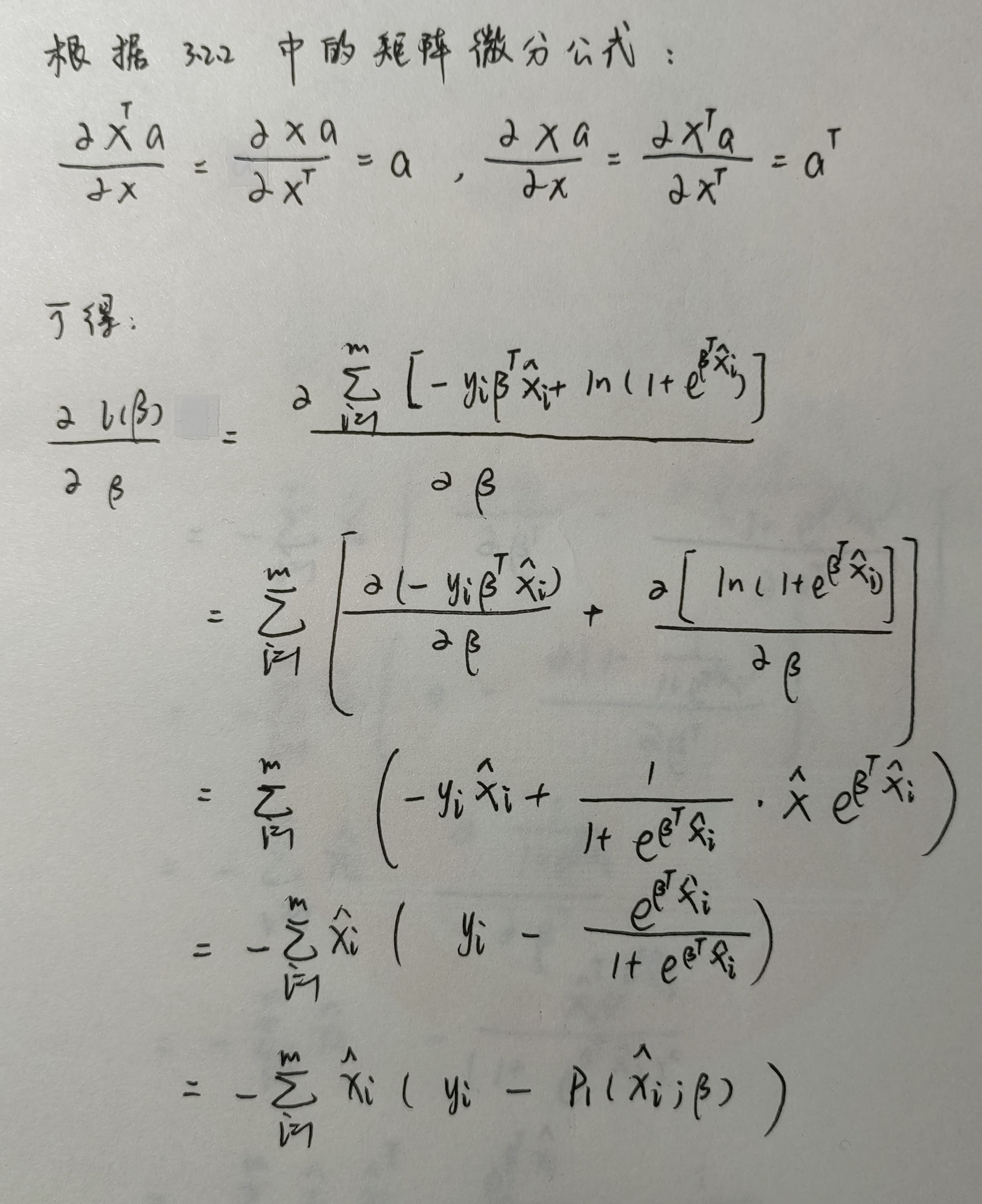
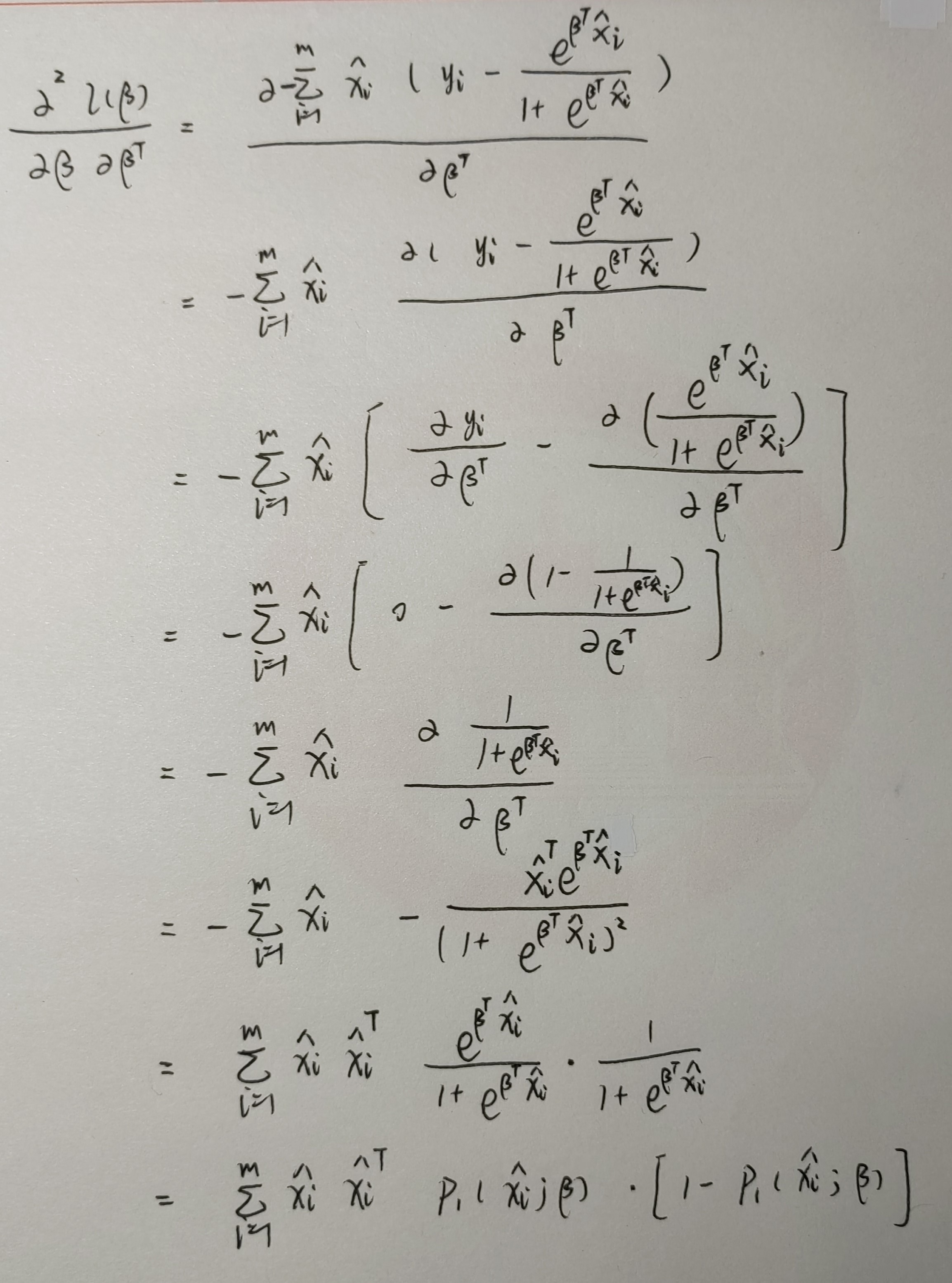
3.4 线性判别分析
线性判别分析的原理是:对于给定的训练集,设法将样本投影到一条直线上,使得同类的投影点尽可能接近,异类样本的投影点尽可能远离;在对新样本进行分类时,将其投影到这条直线上,再根据投影点的位置来确定新样本的类别。
3.5 多分类学习
我们一般采用多分类+集成的策略来解决多分类的学习任务。具体的学习任务大概是:将多分类任务拆分为多个二分类任务,每一个二分类任务训练一个学习器;在测试数据时,将所有的分类器进行集成以获得最终的分类结果。这里有两个关键点:如何拆分多分类任务?如何集成二分类学习器?集成策略见第 8 章,本目主要介绍多分类学习任务的拆分。主要有三种拆分策略:一对多、一对其余、多对多。对于 N 个类别而言:
3.5.1 一对一

- 名称:One vs. One,简称 OvO
- 训练:需要对 N 个类别进行
N ( N − 1 ) 2 \frac{N(N-1)}{2} N ( N − 1 ) 2 \frac{N(N-1)}{2} - 测试:对于一个样本进行分类预测时,需要用
N ( N − 1 ) 2 \frac{N(N-1)}{2} - 特点:类别较少时,时间和内存开销往往更大;类别较多时,时间开销往往较小
3.5.2 一对其余

- 名称:One vs. Rest,简称 OvR
- 训练:需要对 N 个类别进行
N N N N - 测试:对于一个样本进行分类预测时,需要用
N N N N
3.5.3 多对多

- 名称:Many vs. Many,简称 MvM
- 训练(编码):对于 N 个类别数据,我们自定义 M 次划分。每次选择若干个类别作为正类,其余类作为反类。每一个样本在 M 个二分类学习器中都有一个分类结果,也就可以看做一个 M 维的向量。m 个样本也就构成了 m 个在 M 维空间的点阵。
- 测试(解码):对于测试样本,对于 M 个学习器同样也会有 M 个类别标记构成的向量,我们计算当前样本与训练集构造的 m 个样本的海明距离、欧氏距离,距离当前测试样本最近的点属于的类别,我们就认为是当前测试样本的类别。
3.5.4 softmax
类似于 M-P 神经元,目的是为了将当前测试样本属于各个类别的概率之和约束为 1。
3.6 类别不平衡问题
在分类任务的数据集中,往往会出现类别不平衡的问题,即使在类别的样本数量相近时,在使用一对其余等算法进行多分类时,也会出现类比不平衡的问题,因此解决类比不平衡问题十分关键。
3.6.1 阈值移动
常规而言,对于二分类任务。我们假设
但是显然,上述假设不总是成立,我们令
根本初衷是为了让
3.6.2 欠采样
即去除过多的样本使得正反例的数量近似,再进行学习。
- 优点:训练的时间开销小
- 缺点:可能会丢失重要信息
典型的算法是:EasyEnsemble
3.6.3 过采样
即对训练集中类别数量较少的样本进行重复采样,再进行学习。
- 缺点:简单的重复采样会导致模型过拟合数据,缺少泛化能力。
典型的算法是:SMOTE
第4章 决策树
4.1 基本流程
决策树算法遵循自顶向下、分而治之的思想。
决策树结构解读:

- 非叶子结点:属性
- 边:属性值
- 叶子结点:分类结果
决策树生成过程:

- 生成结点:选择最优的属性作为当前结点决策信息
- 产生分支:根据结点属性,为测试数据所有可能的属性值生成一个分支
- 生成子结点:按照上述分支属性对当前训练样本进行划分
- 不断递归:不断重复上述 1-3 步直到递归终点
- 递归终点:共三种(存疑)
- 当前结点的训练样本类别均属于某个类别。则将当前结点设定为叶子结点,并标记当前叶子结点对应的类别为当前结点同属的类别
- 当前结点的训练样本数为
0 0 - 当前结点的训练样本的所有属性值都相同。则将当前结点设定为叶子结点,并标记当前叶子结点对应的类别为当前训练样本中最多类别数量对应的类别
4.2 划分选择
现在我们解决 4.1 节留下的坑,到底如何选择出当前局面下的最优属性呢?我们从“希望当前结点的所包含的样本尽可能属于同一类”的根本目的出发,讨论三种最优属性选择策略。
4.2.1 信息增益
第一个问题:如何度量结点中样本的纯度? 我们引入 信息熵 (information entropy) 的概念。显然,信息熵越小,分支结点的纯度越高;信息熵越大,分支结点的纯度越低。假设当前样本集合中含有
第二个问题:如何利用结点纯度选择最优属性进行划分? 我们引入 信息增益 (Information gain) 的概念。显然,我们需要计算每一个属性对应的信息增益,然后取信息增益最大的属性作为当前结点的最优划分属性。假设当前结点对应的训练数据集为
代表算法:ID3
为了更好的理解信息增益的表达式,我们从终极目标考虑问题。我们知道,决策树划分的终极目的是尽可能使得子结点中的样本纯度尽可能高。对于当前已知的结点,信息熵已经是一个定值了,只有通过合理的划分子结点才能使得整体的熵减小,因此我们从划分后熵减的理念出发,得到了信息增益的表达式。并且得出熵减的结果(信息增益)越大,对应的属性越优。
4.2.2 增益率
由于信息增益会在属性的取值较多时有偏好,因此我们引入 增益率 (Gain ratio) 的概念来减轻这种偏好。显然,增益率越大越好
我们定义增益率为:
可以看到就是将信息增益除上了一个值
一般而言,属性的属性取值越多,信息增益越大,对应的
代表算法:C4.5
4.2.3 基尼指数
最后引入一种最优划分策略:使用 基尼指数 (Gini index) 来划分。基尼指数越小越好。假设当前样本集合中含有
于是属性
代表算法:CART
4.3 剪枝处理
处理过拟合的策略:剪枝。
4.3.1 预剪枝
基于贪心的思想,决策每次划分是否需要进行。我们知道最佳属性的选择是基于信息增益等关于结点纯度的算法策略,而是否进行子结点的生成需要我们进行性能评估,即从测试精度的角度来考虑。因此决策划分是否进行取决于子结点生成前后在验证集上的测试精度,如果可以得到提升则进行生成,反之则不生成子结点,也就是预剪枝的逻辑。
4.3.2 后剪枝
同样是预剪枝的精度决策标准。我们在一个决策树完整生成以后,从深度最大的分支结点开始讨论是否可以作为叶子结点,也就是是否删除该分支的子结点。决策的依据是删除子结点前后在测试集上的精度是否有提升,如果有则删除子结点,反之不变。
4.3.3 区别与联系(补)
预剪枝是基于贪心,也就是说没有考虑到全局的情况,可能出现当前结点划分后测试精度下降,但是后续结点继续划分会得到性能提升,从而导致预剪枝的决策树泛化性能下降。
后剪枝就可以规避贪心导致的局部最优。但是代价就是时间开销更大。
4.4 连续与缺失值
4.4.1 连续值处理
这里讲解二分法 (bi-partition)。主要就是在计算信息增益时增加了一步,将属性的取值情况划分为了两类。那么如何划分呢?关键在于划分点的取值。假设当前属性 a 的取值是连续值,去重排序后得到 n 个数值,我们取这 n 个数值的 n-1 个间隔的中值作为划分点集合,枚举其中的每一个划分点计算最大信息增益,对应的划分点就是当前连续取值的属性的二分划分点。时间复杂度极高!也不知道 C4.5 算法怎么想的
4.4.2 缺失值处理
当然我们可以直接删除含有缺失信息的样本,但是这对数据信息过于浪费,尤其是当数据量不大时,如何解决这个问题呢?我们需要解决两个问题:
- 在选择最优划分属性时,如何计算含有缺失值的属性对应的信息增益呢?
- 在得到最优划分属性时,如何将属性值缺失的样本划分到合理的叶子结点呢?
对于第一个问题:只计算属性值没有缺失的样本,然后放缩到原始的数据集合大小即可
对于第二个问题:对于已知属性值的样本,我们可以计算出每一个属性值的样本数量,从而计算出一个集合比例,这样对于未知属性值的样本,只需要按照前面计算出来的集合,按照概率划分到对应的子结点即可
4.5 多变量决策树
很好,本目就是来解决上述连续值处理的过高时间复杂度的问题的。现在对于一个结点,不是选择最优划分属性,而是对建一个合适的线性分类器,如图:

第5章 神经网络
5.1 神经元模型

我们介绍 M-P 神经元模型。该神经元模型必须具备以下三个特征:
- 输入:来自其他连接的神经元传递过来的输入信号
- 处理:输入信号通过带权重的连接进行传递,神经元接受到所有输入值的总和,再与神经元的阈值进行比较
- 输出:通过激活函数的处理以得到输出
激活函数可以参考 3.3 中的逻辑函数(logistic function),此处将其声明为 sigmoid 函数,同样不采用不。连续光滑的分段函数。
5.2 感知机与多层网络
本目从无隐藏层的感知机出发,介绍神经网络在简单的线性可分问题上的应用;接着介绍含有一层隐藏层的多层感知机,及其对于简单的非线性可分问题上的应用;最后引入多层前馈神经网络模型的概念。
5.2.1 感知机

感知机(Perceptron)由两层神经元组成。第一层是输入层,第二层是输出层。其中只有输出层的神经元为功能神经元,也即 M-P 神经元。先不谈如何训练得到上面的
通过单层的感知机,我们可以实现简单的线性可分的分类任务,比如逻辑运算中的 与、或、非 运算,下面演示一下如何使用单层感知机实现上述三种逻辑运算:
与运算、或运算是二维线性可分任务,一定可以找到一条直线将其划分为两个类别:

非运算是一维线性可分任务,同样也可以找到一条直线将其划分为两个类别:

5.2.2 多层感知机

所谓的多层感知机其实就是增加了一个隐藏层,则神经网络模型就变为三层,含有一个输入层,一个隐藏层,和一个输出层,更准确的说应该是“单隐层网络”。其中隐藏层和输出层中的所有神经元均为功能神经元。
为了学习出网络中的连接权

5.2.3 多层前馈神经网络

所谓多层前馈神经网络,定义就是各层神经元之间不会跨层连接,也不存在同层连接,其中:
- 输入层仅仅接受外界输入,没有函数处理功能
- 隐藏层和输出层进行函数处理
5.3 误差逆传播算法
多层网络的学习能力比感知机的学习能力强很多。想要训练一个多层网络模型,仅仅通过感知机的参数学习规则是不够的,我们需要一个全新的、更强大的学习规则。这其中最优秀的就是误差逆传播算法(errorBackPropagation,简称 BP),往往用它来训练多层前馈神经网络。下面我们来了解一下 BP 算法的内容、参数推导与算法流程。
5.3.1 模型参数
我们对着神经网络图,从输入到输出进行介绍与理解:

- 隐层:对于隐层的第
h h - 输入:
α h = ∑ i = 1 d x i v i h \alpha_h = \sum_{i=1}^dx_i v_{ih} - 输出:
b h = f ( α h − γ h ) b_h = f(\alpha_h - \gamma_h)
- 输入:
- 输出层:对于输出层的第
j j - 输入:
β j = ∑ h = 1 q b h w h j \beta_j=\sum_{h=1}^q b_h w_{hj} - 输出:
y ^ j = f ( β j − θ j ) \hat y_j = f(\beta j - \theta_j)
- 输入:
现在给定一个训练集学习一个分类器。其中每一个样本都含有
- 输入层到隐层的
d × q d \times q v i h ( i = 1 , 2 , ⋯ , d , h = 1 , 2 , ⋯ , q ) v_{ih}(i=1,2,\cdots,d,\ h=1,2,\cdots,q) - 隐层的
q q γ h ( h = 1 , 2 , ⋯ , q ) \gamma_h(h=1,2,\cdots,q) - 隐层到输出层的
q × l q\times l w h j ( h = 1 , 2 , ⋯ , q , j = 1 , 2 , ⋯ , l ) w_{hj}(h=1,2,\cdots,q,\ j=1,2,\cdots,l) - 输出层的
l l θ j ( j = 1 , 2 , ⋯ , l ) \theta_j(j=1,2,\cdots,l)
5.3.2 参数推导
确定损失函数。
对于上述 4 种参数,我们均采用梯度下降策略。以损失函数的负梯度方向对参数进行调整。每次输入一个训练样本,都会进行一次参数迭代更新,这叫标准 BP 算法。
根本目标是使损失函数尽可能小,我们定义损失函数
E E 1 2 \frac{1}{2} k k
确定迭代修正量。
假定当前学习率为
η \eta w h j ← w h j + Δ w h j θ j ← θ j + Δ θ j v i h ← v i h + Δ v i h γ h ← γ h + Δ γ h \begin{aligned}w_{hj} &\leftarrow w_{hj}+\Delta w_{hj} \\\theta_{j} &\leftarrow \theta_{j}+\Delta \theta_{j} \\v_{ih} &\leftarrow v_{ih}+\Delta v_{ih} \\\gamma_{h} &\leftarrow \gamma_{h}+\Delta \gamma_{h} \\\end{aligned} 其中,修正量分别为:
Δ w h j = η g j b h Δ θ j = − η g j Δ v i h = η e h x i Δ γ h = − η e h \begin{aligned}\Delta w_{hj} &= \eta g_j b_h \\\Delta \theta_{j} &= -\eta g_j \\\Delta v_{ih} &= \eta e_h x_i \\\Delta \gamma_{h} &= -\eta e_h \\\end{aligned}
公式表示:

隐层到输出层的权重、输出神经元的阈值:

输入层到隐层的权重、隐层神经元的阈值:

5.3.3 算法流程
对于当前样本的输出损失

还有一种 BP 神经网络方法就是累计 BP 神经网络算法,基本思路就是对于全局训练样本计算累计误差,从而更新参数。在实际应用过程中,一般先采用累计 BP 算法,再采用标准 BP 算法。还有一种思路就是使用随机 BP 算法,即每次随机选择一个训练样本进行参数更新。
第6章 支持向量机
依然是分类学习任务。我们希望找到一个超平面将训练集中样本划分开来,那么如何寻找这个超平面呢?下面开始介绍。
本章知识点逻辑链:

6.1 间隔与支持向量
对于只有两个特征,输出只有两种状态的训练集而言,很显然我们得到如下图所示的超平面,并且显然应该选择最中间的泛化能力最强的那一个超平面:

我们定义超平面为:
定义支持向量机为满足下式的样例:
很显然,为了求得这“最中间”的超平面,就是让异类支持向量机之间的距离尽可能的大,根据两条平行线距离的计算公式,可知间隔为:
于是最优化目标函数就是:
可以等价转化为:
这就是 SVM(support vector machine)的基本型
6.2 对偶问题
将上述 SVM 基本型转化为对偶问题,从而可以更高效的求解该最优化问题。


于是模型
其中参数 b 的求解可通过支持向量得到:
由于原问题含有不等式约束,因此还需要满足 KKT 条件:
对于上述互补松弛性:
- 若
α i > 0 \alpha_i > 0 y i f ( x i ) = 1 y_if(x_i)=1 - 若
y i f ( x i ) > 1 y_if(x_i)>1 α i = 0 \alpha_i = 0
现在得到的对偶问题其实是一个二次规划问题,我们可以采用 SMO(Sequential Minimal Optimization) 算法求解。具体略。
6.3 核函数
对原始样本进行升维,即

表格中的高斯核也就是所谓的径向基函数核
- 当
γ \gamma exp ( − γ ∥ x i − x j ∥ 2 ) \exp(-\gamma \|x_i - x_j\|^2) - 当
γ \gamma exp ( − γ ∥ x i − x j ∥ 2 ) \exp(-\gamma \|x_i - x_j\|^2)
6.4 软间隔与正则化
对于超平面的选择,其实并不是那么容易,并且即使训练出了一个超平面,我们也不知道是不是过拟合产生的,因此我们需要稍微减轻约束条件的强度,因此引入软间隔的概念。
我们定义软间隔为:某些样本可以不严格满足约束条件
常见的平滑连续的替代损失函数为:

我们引入松弛变量
6.5 支持向量回归
支持向量回归(Support Vector Regression,简称 SVR)与传统的回归任务不同,传统的回归任务需要计算每一个样本的误差,而支持向量回归允许有一定的误差,即,仅仅计算落在隔离带外面的样本损失。
原始问题:


对偶问题:
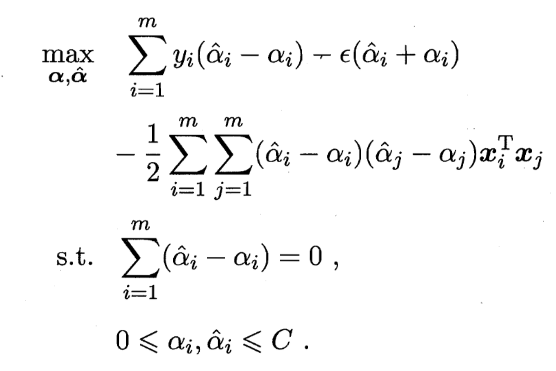
KKT 条件:
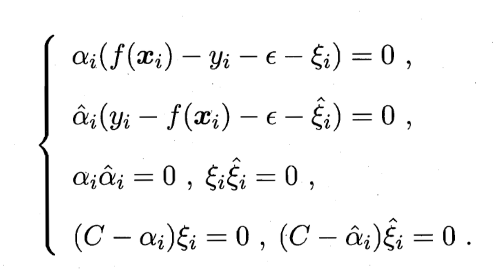
预测模型:

6.6 核方法
通过上述:支持向量基本型、支持向量软间隔化、支持向量回归,三个模型的学习,可以发现最终的预测模型都是关于核函数与拉格朗日乘子的线性组合,那么这是巧合吗?并不是巧合,这其中其实有一个表示定理:
第7章 贝叶斯分类器
7.1 贝叶斯决策论
pass
7.2 极大似然估计
根本任务:寻找合适的参数
我们定义对数似然
此时参数
7.3 朴素贝叶斯分类器
我们定义当前类别为
现在假设各属性之间相互独立,则对于拥有 d 个属性的训练集,在利用贝叶斯定理时,可以通过连乘的形式计算类条件概率
注意点:
- 对于离散数据。上述类条件概率的计算方法很好计算,直接统计即可
- 对于连续数据。我们就没法直接统计数据数量了,替换方法是使用高斯函数。我们根据已有数据计算得到一个对于当前属性的高斯函数,后续计算测试样例对应属性的条件概率,代入求得的高斯函数即可。
- 对于类条件概率为 0 的情况。我们采用拉普拉斯修正。即让所有属性的样本个数
+ 1 +1 + d +d 1 1
7.4 半朴素贝叶斯分类器
朴素贝叶斯的问题是假设过于强,现实不可能所有的属性都相互独立。半朴素贝叶斯弱化了朴素贝叶斯的假设。现在假设每一个属性最多只依赖一个其他属性。即独依赖估计
如何寻找依赖关系?我们从属性依赖图出发

如上图所示:
- 朴素贝叶斯算法中:假设所有属性相互独立,因此各属性之间没有连边
- SPODE 确定属性父属性算法中:假设所有属性都只依赖于一个属性(超父),我们只需要找到超父即可
- TAN 确定属性父属性算法中:我们需要计算每一个属性之间的互信息,最后得到一个以互信息为边权的完全图。最终选择最大的一些边构成一个最大带权生成树
- AODE 确定属性父属性算法中:采用集成的思想,以每一个属性作为超父属性,最后选择最优即可
7.5 贝叶斯网
构造一个关于属性之间的 DAG 图,从而进行后续类条件概率的计算。三种典型依赖关系:
| 同父结构 | V型结构 | 顺序结构 |
|---|---|---|
 |  |  |
| 在已知 | 若 | 在已知 |
概率计算公式参考:超详细讲解贝叶斯网络(Bayesian network)
7.6 EM 算法
现在我们需要解决含有隐变量
- E-step:首先利用观测数据
X X Θ t \Theta_t Z t Z^t - M-step:接着对
X X Z t Z^t Θ t + 1 \Theta_{t+1}
有两个问题:哪来的参数?什么时候迭代终止?
- 对于第一个问题:我们随机化初始得到参数
Θ 0 \Theta_0 - 对于第二个问题:相邻两次迭代结果中参数差值的范数小于阈值
( ∣ ∣ θ ( i + 1 ) − θ ( i ) ) ∣ ∣ < ϵ 1 ) (|| \theta^{(i+1)} - \theta^{(i)}) || < \epsilon_1) ( ∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ < ϵ 2 ) (|| Q(\theta^{(i+1)} , \theta^{(i)})) - Q(\theta^{(i)} , \theta^{(i)}) || < \epsilon_2)
第8章 集成学习
8.1 个体与集成
集成学习由多个不同的组件学习器组合而成。学习器不能太坏并且学习器之间需要有差异。如何产生并结合“好而不同”的个体学习器是集成学习研究的核心。集成学习示意图如下:

根据个体学习器的生成方式,目前集成学习可分为两类,代表作如下:
- 个体学习器直接存在强依赖关系,必须串行生成的序列化方法:Boosting
- 个体学习器间不存在强依赖关系,可以同时生成的并行化方法:Bagging 和 随机森林 (Random Forest)
8.2 Boosting
Boosting 算法族的逻辑:
- 个体学习器之间存在强依赖关系
- 串行生成每一个个体学习器
- 每生成一个新的个体学习器都要调整样本分布
以 AdaBoost 算法为例,问题式逐步深入算法实现:
如何计算最终集成的结果?利用加性模型 (additive model),假定第
i i h ( x ) h(x) i i α i \alpha_i H ( x ) H(x) H ( x ) = sign ( ∑ i = 1 T α i h i ( x ) ) H(x) = \text{sign} \left(\sum_{i=1}^T \alpha_i h_i(x)\right) 如何确定每一个学习器的权重
α i \alpha_i α i = 1 2 ln ( 1 − ϵ i ϵ i ) \displaystyle \alpha_i=\frac{1}{2}\ln (\frac{1-\epsilon_i}{\epsilon_i}) 如何调整样本分布?我们对样本进行赋权。学习第一个学习器时,所有的样本权重相等,后续学习时的样本权重变化规则取决于上一个学习器的分类情况。上一个分类正确的样本权重减小,上一个分类错误的样本权重增加,即:
D i + 1 ( x ) = D i ( x ) Z i × { e − α i , h i ( x ) = f ( x ) e α i , h i ( x ) ≠ f ( x ) D_{i+1}(x) = \frac{D_i(x)}{Z_i} \times \begin{cases}e^{-\alpha_i}&,h_i(x)=f(x) \\e^{\alpha_i}&,h_i(x)\ne f(x)\end{cases}
代表算法:AdaBoost、GBDT、XGBoost
8.3 Bagging 与 随机森林
在指定学习器个数
8.3.1 Bagging
问题式逐步深入 Bagging 算法实现:
- 如何计算最终集成的结果?直接进行大数投票即可,注意每一个学习器都是等权重的
- 如何选择每一个训练器的训练样本?顾名思义,就是进行
T T - 如何选择基学习器?往往采用决策树 or 神经网络
8.3.2 随机森林
问题式逐步深入随机森林 (Random Forest,简称 RF) 算法实现:
- 如何计算最终集成的结果?直接进行大数投票即可,注意每一个学习器都是等权重的
- 为什么叫森林?每一个基学习器都是「单层」决策树
- 随机在哪?首先每一个学习器对应的训练样本都是随机的,其次每一个基学习器的属性都是随机的
k ( k ∈ [ 1 , V ] ) k(k \in [1,V])
8.3.3 区别与联系(补)
区别:随机森林与 Bagging 相比,多增加了一个属性随机,进而提升了不同学习器之间的差异度,进而提升了模型性能,效果如下:

联系:两者均采用自助采样法。优势在于,不仅解决了训练样本不足的问题,同时 T 个学习器的训练样本之间是有交集的,这也就可以减小测试的方差。
8.4 区别与联系(补)
区别:
- 序列化基学习器最终的集成结果往往采用加权投票
- 并行化基学习器最终的集成结果往往采用平权投票
联系:
- 序列化减小偏差。即可以增加拟合性,降低欠拟合
- 并行化减小方差。即可以减少数据扰动带来的误差
8.5 结合策略
基学习器有了,如何确定最终模型的集成输出呢?我们假设每一个基学习器对于当前样本
8.5.1 平均法
对于数值型输出
- 简单平均法:
H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(x) = \displaystyle \frac{1}{T} \sum_{i =1}^T h_i(x) - 加权平均法:
H ( x ) = ∑ i = 1 T w i h i ( x ) , w i ≥ 0 , ∑ i = 1 T w i = 1 H(x) = \displaystyle\sum_{i=1}^T w_i h_i(x),\quad w_i \ge 0, \sum_{i=1}^Tw_i = 1
显然简单平均法是加权平均法的特殊。一般而言,当个体学习器性能差距较大时采用加权平均法,相近时采用简单平均法。
8.5.2 投票法
对于分类型输出
- 绝对多数投票法:选择超过半数的,如果没有则拒绝投票
- 相对多数投票法:选择票数最多的,如果有多个相同票数的则随机取一个
- 加权投票法:每一个基学习器有一个权重,从而进行投票
8.5.3 学习法
其实就是将所有基学习器的输出作为训练数据,重新训练一个模型对输出结果进行预测。其中,基学习器称为“初级学习器”,输出映射学习器称为“次级学习器”或”元学习器”
其中
- Stacking
- 多响应线性回归
(Mutil-response linear regression, 简称 MLR) \text{(Mutil-response linear regression, 简称 MLR)} - 贝叶斯模型平均
(Bayes Model Averaging, 简称 BMA) \text{(Bayes Model Averaging, 简称 BMA)}
经过验证,Stacking 的泛化能力往往比 BMA 更优。
8.6 多样性
8.6.1 误差-分歧分解
根据「回归」任务的推导可得下式。其中
8.6.2 多样性度量
如何估算个体学习器的多样化程度呢?典型做法是考虑两两学习器的相似性。所有指标都是从两个学习器的分类结果展开,以两个学习器

显然
- 不合度量
- 相关系数
- Q-统计量
κ \kappa
以「
- 串行的基学习器多样性较并行的基学习器更高
- 串行的基学习器误差较并行的基学习器也更高

8.6.3 多样性增强
为了训练出多样性大的个体学习器,我们引入随机性。介绍几种扰动策略:
- 数据样本扰动
- 输入属性扰动
- 输出表示扰动
- 算法参数扰动
第9章 聚类
9.1 聚类任务
典型的无监督学习方法。即将众多无标签数据进行分类。在开始介绍几类经典的聚类学习方法之前,我们先讨论聚类算法涉及到的两个基本问题:性能度量和距离计算。
9.2 性能度量
一来是进行聚类的评估,二来也可以作为聚类的优化目标。分为两种,分别是外部指标和内部指标。
9.2.1 外部指标
所谓外部指标就是已经有一个“参考模型”存在了,将当前模型与参考模型的比对结果作为指标。我们考虑两两样本的聚类结果,定义下面的变量:
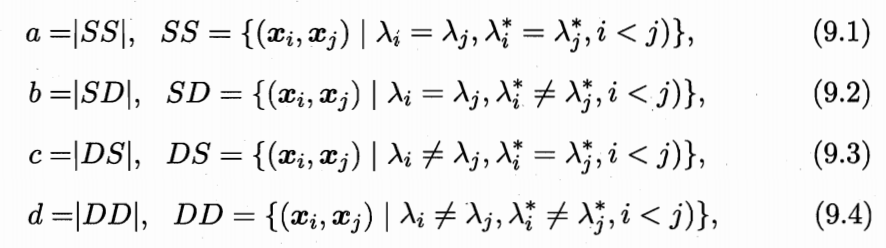
显然
- JC 指数:
J C = a a + b + c \displaystyle JC = \frac{a}{a+b+c} - FM 指数:
a a + b ⋅ a a + c \displaystyle \sqrt{\frac{a}{a+b} \cdot \frac{a}{a+c}} - RI 指数:
2 ( a + d ) m ( m − 1 ) \displaystyle \frac{2(a+d)}{m(m-1)}
上述指数取值均在
9.2.2 内部指标
所谓内部指标就是仅仅考虑当前模型的聚类结果。同样考虑两两样本的聚类结果,定义下面的变量:
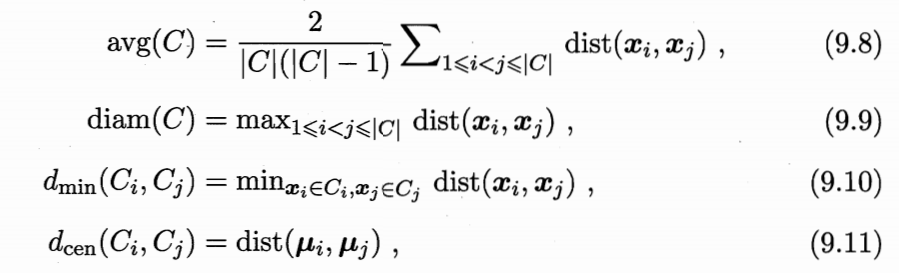
常见的外部指标如下:
- DB 指数
- Dunn 指数
9.3 距离计算
有序属性:闵可夫斯基距离
无序属性:VDM 距离
9.4 原型聚类
9.4.1 k 均值算法
算法流程大体上可以归纳为三步:
- 初始化 k 个聚类中心
- 枚举所有样本并将其划分到欧氏距离最近的中心
- 更新 k 个簇中心
重复上述迭代过程直到聚类中心不再发生变化,当然为了防止迭代时间过久,可以弱化迭代终止条件,比如增设:最大迭代论述或对聚类中心的变化增加一个阈值而非绝对的零变化。k 均值算法伪代码如下:

9.4.2 学习向量量化算法
9.4.3 高斯混合聚类算法

9.5 密度聚类
DBSCAN 算法
适用于簇的大小不定,距离不定的情况。大概就是多源有向bfs的过程。定义每一源为“核心对象”,每次以核心对象为起始进行bfs,将每一个符合“范围约束”的近邻点纳入当前簇,不断寻找知道所有核心对象都访问过为止。
9.6 层次聚类
AGNES 算法
适用于可选簇大小、可选簇数量的情况。
第10章 降维与度量学习
本章我们通过 k 近邻监督学习方法引入「降维」和「度量学习」的概念。
- 对于降维算法:根本原因是样本往往十分稀疏,需要我们对样本的属性进行降维,从而达到合适的密度进而可以进行基于距离的邻居选择相关算法。我们将重点讨论以下几个降维算法:MDS 多维缩放、PCA 主成分分析、等度量映射
- 对于度量学习:上述降维的根本目的是选择合适的维度,确保一定可以通过某个距离计算表达式计算得到每一个样本的 k 个邻居。而度量学习直接从目的出发,尝试直接学习样本之间的距离计算公式。我们将重点讨论以下几个度量学习算法:近邻成分分析、LMNN
10.1 k 近邻学习
k 近邻(k-Nearest Neighbor,简称 KNN)是一种监督学习方法。一句话概括就是「近朱者赤近墨者黑」,每一个测试样本的分类或回归结果取决于在某种距离度量下的最近的 k 个邻居的性质。不需要训练,可以根据检测样本实时预测,即懒惰学习。为了实现上述监督学习的效果,我们需要解决以下两个问题:
- 如何确定「距离度量」的准则?就那么几种,一个一个试即可。
- 如何定义「分类结果」的标签?分类任务是 k 个邻居中最多类别的标签,回归任务是 k 个邻居中最多类别标签的均值。
上述学习方法有什么问题呢?对于每一个测试样例,我们需要确保能够通过合适的距离度量准则选择出 k 个邻居出来,这就需要保证数据集足够大。在距离计算时,每一个属性都需要考虑,于是所需的样本空间会呈指数级别的增长,这被称为「维数灾难」。这是几乎不可能获得的数据量同时在进行矩阵运算时时间的开销也是巨大的。由此引入本章的关键内容之一:降维。
为什么能降维?我们假设学习任务仅仅是高维空间的一个低维嵌入。
10.2 多维缩放降维
「多维缩放(MDS)降维算法」的原则:对于任意的两个样本,降维后两个样本之间的距离保持不变。
基于此思想,可以得到以下降维流程:我们定义
内积计算:

新属性值计算:特征值分解法。其中

10.3 主成分分析降维
「主成分分析(Principal Component Analysis,简称 PCA)降维算法」的两个原则:
- 样本到超平面的距离都尽可能近
- 样本在超平面的投影都尽可能分开
基于此思想可以得到 PCA 的算法流程:

假设我们有一个简单的数据集
我们希望将这些样本从二维空间降维到一维空间(即
步骤 1: 样本中心化
首先计算样本的均值向量:
然后对所有样本进行中心化:
步骤 2: 计算协方差矩阵
样本的协方差矩阵为:
步骤 3: 对协方差矩阵进行特征值分解
协方差矩阵的特征值分解:
特征值为
步骤 4: 取最大的
我们选择最大的特征值对应的特征向量
10.4 核化线性降维
「核化线性降维算法」的原则:pass
10.5 流形学习降维
假定数据满足流形结构。
10.5.1 等度量映射
流形样本中,直接计算两个样本之间的欧式距离是无效的。我们引入「等度量映射」理念。根本算法逻辑是:利用最短路算法计算任意两个样本之间的「测地线距离」得到
10.5.2 局部线性嵌入
pass
10.6 度量学习
降维的本质是寻找一种合适的距离度量方法,与其降维为什么不直接学习一种距离计算方法呢?我们引入「度量学习」的理念。
为了“有参可学”,我们需要定义距离计算表达式中的超参,我们定义如下「马氏距离」:
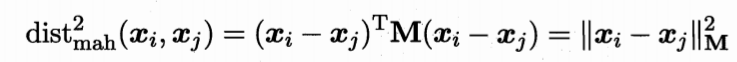
为什么用所谓的马氏距离呢?欧氏距离不行吗?我们有以下结论:
- 欧式距离具有旋转不变性和平移不变性,在低维和属性直接相互独立时是最佳实践。但是当属性之间有相关性并且尺度相差较大时,直接用欧式距离计算会丢失重要的特征之间的信息;
- 马氏距离具有尺度不变性,在高维和属性之间有关系且尺度不同时是最佳实践。缺点在于需要计算协方差矩阵导致计算量远大于欧氏距离的计算量。
下面介绍两种度量学习算法来学习上述 M 矩阵,也就是数据集的「协方差矩阵的逆」中的参数。准确的说是学习一个矩阵来近似代替协方差矩阵的逆矩阵。
10.6.1 近邻成分分析
近邻成分分析
10.6.2 LMNN
大间隔最近邻
paper: Distance Metric Learning for Large Margin Nearest Neighbor Classification
explain: 【LMNN】浅析"从距离测量到基于Margin的邻近分类问题"
第13章 半监督学习
半监督学习的根本目标:同时利用有标记和未标记样本的数据进行学习,提升模型泛化能力。主要分为三种:
- 主动学习
- 纯半监督学习
- 直推学习

13.1 未标记样本
对未标记数据的分布进行假设,两种假设:
- 簇状分布
- 流形分布
13.2 生成式方法
分别介绍「生成式方法」和「判别式方法」及其区别和联系。
生成式方法:核心思想就是用联合分布
- 朴素贝叶斯
- 高斯混合聚类
- 马尔科夫模型
判别式方法:核心思想就是用条件分布
- 线性回归
- 逻辑回归
- 决策树
- 神经网络
- 支持向量机
- 条件随机场
自监督训练(补)
根本思想就是利用有标记数据进行模型训练,然后对未标记数据进行预测,选择置信度较高的一些样本加入训练集重新训练模型,不断迭代进行直到最终训练出来一个利用大量未标记数据训练出来的模型。
如何定义置信度高?我们利用信息熵的概念,即对于每一个测试样本都有一个预测向量,信息熵越大表明模型对其的预测结果越模糊,因此置信度高正比于信息熵小,将信息熵较小的测试样本打上「伪标记」加入训练集。
13.3 半监督 SVM
以经典 S3VM 中的经典算法 TSVM 为例。给出优化函数、算法图例、算法伪代码:
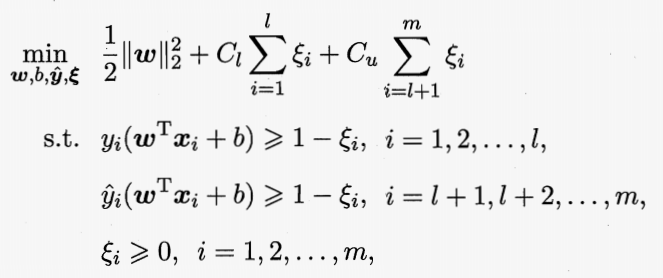


13.4 图半监督学习
同样解决分类问题,以「迭代式标记传播算法」为例。
二分类,可以直接求出闭式解。
算法逻辑。每一个样本对应图中的一个结点,两个结点会连上一个边,边权正比于两结点样本的相似性。最终根据图中已知的某些结点进行传播标记即可。与基于密度的聚类算法类似,区别在于此处不同的簇 cluster 可能会对应同一个类别 class。
如何进行连边?不会计算每一个样本的所有近邻,一般采用局部近邻选择连边的点,可以 k 近邻,也可以范围近邻。
优化函数。定义图矩阵的能量损失函数为图中每一个结点与所有结点的能量损失和,目标就是最小化能量损失和:
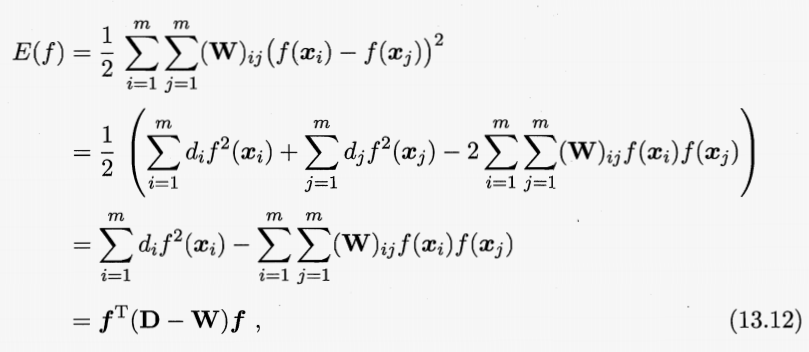
多分类,无法直接求出闭式解,只能进行迭代式计算。
新增变量。我们定义标记矩阵 F,其形状为

13.5 基于分歧的方法
多学习器协同训练。
第14章 概率图模型
为了分析变量之间的关系,我们建立概率图模型。按照图中边的性质可将概率图模型分为两类:
- 有向图模型,也称贝叶斯网
- 无向图模型,也称马尔可夫网
14.1 隐马尔可夫模型
隐马尔可夫模型
需要解决三个问题:
- 如何评估建立的网络模型和实际观测数据的匹配程度?
- 如果上面第一个问题中匹配程度不好,如何调整模型参数来提升模型和实际观测数据的匹配程度呢?
- 如何根据实际的观测数据利用网络推断出有价值的隐藏状态?
14.2 马尔科夫随机场
马尔科夫随机场
联合概率计算逻辑按照势函数和团展开。其中团可以理解为完全子图;极大团就是结点最多的完全子图,即在当前的完全子图中继续添加子图之外的点就无法构成新的完全子图;势函数就是一个关于团的函数。
14.3 条件随机场
判别式方法。
14.4 学习和推断
精确推断。
14.5 近似推断
近似推断。降低计算时间开销。
- 采样法:蒙特卡洛采样法
- 变分推断:考虑近似分布
考试大纲
- 单选
10 * 3':单选直接一个单刀咆哮。注意审题、注意一些绝对性的语句; - 简答
4 * 5':想拿满分就需要写出理论对应的具体公式; - 计算
3 * 10':老老实实写每一个计算过程,不要跳步骤; - 论述
2 * 10':没考过,大约是简答题加强版。注意逻辑一定要清晰。
前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 段博佳 | 3 | 自发课 |
成绩组成:
| 平时(5次作业+签到) | 期末(书本+讲义) |
|---|---|
| 60% | 40% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 算法设计与分析 | 《算法设计与分析(python版)》 | 1 | 王秋芬 | 清华大学出版社 | 978-7-302-57072-1 |
一、贪心
Dijkstra、Prim、Kruskal、Huffman
二、分治
二分、归并、快排(第 k 个数)
三、动规
- 区间dp:矩阵连乘
- 网格图dp:LCS
- 背包:完全背包、多重背包
四、深搜
- 排列树:TSP、图染色、调度、n 皇后
- 子集树:01背包
考后碎碎念
考的中规中矩,但是忘带修正带导致卷面一坨hh。按照试卷顺序罗列一下:表达式树、大根堆、Dijkstra、图染色、第 k 个数、Kruskal、完全背包。
试卷一看就是 wq 出的,但还是用 python 写的代码。有一说一这次考试还加深了我对快排的理解,尤其是在让我给出分治后的序列时hh。硬要按照上面四个标签分类的话大概就是:
- 贪心:Dijkstra、Kruskal
- 分治:第 k 个数
- 动规:完全背包
- 深搜:表达式树、大根堆、图染色
前言
学科情况:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 周效尧 | 4 | 学科基础课 |
成绩组成:
| 平时 | 测验(×2) | 期末 |
|---|---|---|
| 10% | 30% | 60% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 概率论与数理统计Ⅰ | 《概率论与数理统计》 | 第一版 | 刘国祥王晓谦 等主编 | 科学出版社 | 978-7-03-038317-4 |
学习资源:
- 📺 视频资源:《概率论与数理统计》教学视频全集(宋浩)
- 📖 教材答案:
- 本地路径(自用):[概率论答案.pdf](D:\华为云盘\2. Score\4. 概率论与数理统计\概率论答案.pdf)
- 网盘资源(共享):提取码:448w
第1章 事件与概率
1.1 随机事件与样本空间
1.1.1 样本空间
随机事件发生的总集合
1.1.2 随机事件
事件是否发生取决于观察结果的事件
1.1.3 事件之间的关系与运算
- 包含:
A ⊂ B A \subset B B ⊂ A B \subset A - 相等:
A = B A=B - 并(和):
A ∪ B A \cup B - 交(积):
A ∩ B ( A B ) A \cap B \quad (AB) - 互斥(互不相容):
A B = Φ AB=\Phi - 对立事件(余事件):
A ∩ B = Φ ∧ A ∪ B = Ω A \cap B=\Phi \land A \cup B=\Omega - 差:
A − B = A ∩ B ‾ = A B ‾ A-B=A \cap \overline{B} = A \overline B - 德摩根律
将事件发生的概率论转化为集合论进行计算与分析
1.2 概率的三种定义及其性质
1.2.1 概率的统计定义
从频率出发得到。
1.2.2 概率的古典定义
特征:
- 样本空间是有限集
- 等可能性(试验中每个基本事件发生的概率是等可能的)
内容:
- 模型与计算公式
- 基本组合分析公式
- 乘法、加法原理
- 排列公式
- 组合公式
- 实例
- 超几何概率
- 分房问题
- 生日问题
- 古典概率的基本性质
1.2.3 概率的几何定义
特征:
- 样本空间不可列
- 等可能性
内容:
- 模型与计算公式
- 实例
- 一维几何图形:公交车乘车问题
- 二维几何图形:会面问题、蒲丰(Buffon)投针问题
- 几何概率的基本性质
1.2.4 概率的性质
pass
1.3 常用概型公式
1.3.1 条件概率计算公式
1.3.2 乘法原理计算公式
基本 : 前提 : P ( A ) > 0 \text{基本}:\text{前提}:P(A)>0 P ( A B ) = P ( A ) P ( B ∣ A ) P(AB) = P(A)P(B|A) 推广 : 前提 : P ( A 1 A 2 , . . . , A n ) > 0 \text{推广}:\text{前提}:P(A_1A_2,...,A_n)>0 P ( A 1 A 2 . . . A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) ⋯ P ( A n ∣ A 1 A 2 . . . A n − 1 ) P(A_1A_2...A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2) \cdots P(A_n|A_1A_2...A_{n-1})
1.3.3 全概公式
我们将样本空间
1.3.4 贝叶斯公式
在上述全概公式的背景之下,现在希望求解事件
可以发现全概公式是计算事件发生的所有子样本空间的概率贡献,而贝叶斯公式是计算事件发生的总概率中某些子样本空间的概率贡献,前者是正向思维,后者是逆向思维
1.4 事件的独立性及伯努利概型
1.4.1 独立性
定义
基本:若
A , B A,B P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) 推广:若
A 1 , A 2 , . . . , A n A_1,A_2,...,A_n ∀ 1 ≤ i 1 < i 2 < ⋯ < i k ≤ n ( k = 2 , 3 , ⋯ , n ) s . t . P ( A i 1 A i 2 ⋯ A i k ) = P ( A i 1 ) P ( A i 2 ) ⋯ P ( A i k ) \begin{aligned}\forall \quad 1 \le i_1<i_2<\cdots<i_k \le n\ (k=2,3,\cdots,n) \\s.t. \quad P(A_{i_1}A_{i_2}\cdots A_{i_k}) = P(A_{i_1})P(A_{i_2})\cdots P(A_{i_k})\end{aligned}
定理
基本:若
A , B A,B A , B ‾ A,\overline{B} A ‾ , B \overline{A},B A ‾ , B ‾ \overline{A},\overline{B} 推广:若
A 1 , A 2 , . . . , A n A_1,A_2,...,A_n k ( 2 ≤ k ≤ n ) k(2 \le k \le n) P ( A i 1 ^ A i 2 ^ ⋯ A i k ^ ) = P ( A i 1 ^ ) P ( A i 2 ^ ) ⋯ P ( A i k ^ ) s . t . A i j ^ = A o r A ‾ ( j = 1 , 2 , ⋯ , k ) \begin{aligned}P(\hat{A_{i_1}}\hat{A_{i_2}}\cdots \hat{A_{i_k}}) = P(\hat{A_{i_1}})P(\hat{A_{i_2}})\cdots P(\hat{A_{i_k}}) \\s.t. \quad \hat{A_{i_j}} = A \ or \ \overline{A}\ (j=1,2,\cdots,k)\end{aligned}
概念辨析
两两独立:对于
n n 相互独立:对于
n n 2 → n 2 \to n 总结:对于
n n C n 2 C_n^2 2 n − ( n + 1 ) 2^n-(n+1) 两两独立 ⊂ 相互独立 \text{两两独立} \subset \text{相互独立}
1.4.2 伯努利概型
定义:
n n n n - 伯努利概型:每次试验只有两种可能的结果
模型:
二项概率公式:n 次独立重复试验发生 k 次的概率:
C n k p k ( 1 − p ) n − k C_n^k p^k (1-p)^{n-k} 几何概率公式:在第 n 次试验首次成功的概率:
( 1 − p ) n − 1 p (1-p)^{n-1}p
第2章 随机事件及其分布
我们知道,解决事件发生概率的问题,除了事件表示以外,我们还关心每一个事件发生的概率
- 首先介绍随机变量的概念以及分布函数的概念
- 接着介绍随机变量对应的概率发生情况组成的集合。离散型的叫分布列,连续型的叫概率密度函数,并在其中贯穿分布函数的应用
- 最后介绍分布函数的复合。从离散型和连续型随机变量两个方向展开
2.1 随机变量及其概率分布
2.1.1 随机变量的概念
总的来说,随机变量就是一个样本空间与实数集的映射。我们定义样本空间
2.1.2 随机变量的分布函数
- 分布函数的定义:
F ( x ) = P ( X ≤ x ) F(x)=P(X \le x) - 分布函数的性质:
- 非负有界性:
0 ≤ F ( x ) ≤ 1 0 \le F(x) \le 1 - 单调不减性:若
x 1 < x 2 x_1 < x_2 F ( x 1 ) ≤ F ( x 2 ) F(x_1) \le F(x_2) F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 \displaystyle F(-\infty) = \lim_{x \to -\infty} F(x) = 0 F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 \displaystyle F(+\infty) = \lim_{x \to +\infty} F(x) = 1 - 右连续性:
lim x → x 0 + F ( x ) = F ( x 0 ) ( − ∞ < x 0 < + ∞ ) \displaystyle \lim_{x\to x_0^+}F(x) = F(x_0)\quad(-\infty < x_0 < +\infty)
- 非负有界性:
2.2 离散型随机变量及其分布列
2.2.1 离散性随机变量的分布列
随机变量的取值都是整数,有以下三种表示方法
公式法
p k = P ( X = x k ) , k = 1 , 2 , ⋯ , p_k = P(X=x_k),\quad k = 1,2,\cdots, 服从法
X ∼ ( x 1 x 2 x 3 ⋯ p 1 p 2 p 3 ⋯ ) X \sim \begin{pmatrix}x_1 & x_2 & x_3 & \cdots \\p_1 & p_2 & p_3 & \cdots\end{pmatrix} 表格法
X x 1 x 2 x 3 ⋯ P p 1 p 2 p 3 ⋯ \begin{array}{c|cccc}X & x_1 & x_2 & x_3 & \cdots \\\hlineP & p_1 & p_2 & p_3 & \cdots\end{array}
2.2.2 常用离散性随机变量及其分布列
0-1分布:即一个事件只有两面性,我们称这样的随机变量服从0-1分布或者两点分布,记作
X ∼ ( 0 1 1 − p p ) X \sim \begin{pmatrix}0 & 1 \\1-p & p\end{pmatrix} 二项分布:其实就是 n 重伯努利试验,我们称这样的随机变量服从二项分布,分布列为
P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k) = C_n^kp^k(1-p)^{n-k} X ∼ B ( n , p ) X \sim B(n,p) 几何分布:同样是伯努利事件,现在需要求解第
k k P ( X = k ) = ( 1 − p ) k − 1 p P(X=k)=(1-p)^{k-1}p X ∼ G ( p ) X \sim G(p) 超几何分布:就是在 N 件含有 M 件次品的样品中无放回的抽取 n 件,问其中含有次品数量的分布列,为
P ( X = k ) = C M k C N − M n − k C N n , k = 0 , 1 , 2 , ⋯ , min ( n , M ) \displaystyle P(X=k)=\frac{C_M^k C_{N-M}^{n-k}}{C_N^n}, \quad k=0,1,2,\cdots,\min{(n, M)} X ∼ 超几何分布 ( n , N , M ) X \sim \text{超几何分布}(n,N,M) 泊松分布:当二项分布中,试验次数很大或者概率很小时,可以近似为泊松分布,即
P ( X = k ) = C n k p k ( 1 − p ) n − k → λ k k ! e − λ \displaystyle P(X=k)=C_n^k p^k(1-p)^{n-k} \to \frac{\lambda^k}{k!}e^{-\lambda} λ > 0 \lambda > 0 X ∼ P ( λ ) X \sim P(\lambda) 显然,泊松分布含有下面两个性质
P ( X = k ) > 0 , k = 0 , 1 , ⋯ P(X=k) > 0,k=0,1,\cdots ∑ k = 0 ∞ P ( X = k ) = 1 \displaystyle \sum_{k=0}^\infty P(X=k)=1 ▶泊松分布正规性证明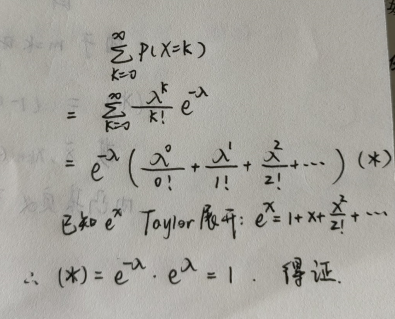
2.3 连续型随机变量及其概率密度函数
说白了其实就是离散性随机变量的积分加强版。现在随着事件发生的不同取值
2.3.1 连续型随机变量的密度函数
概率密度函数,简称:密度函数 or 概率密度
定义:设随机变量
X X F ( x ) F(x) p ( x ) p(x) X X p ( x ) p(x) X X ∀ x ∈ R , F ( x ) = ∫ − ∞ x p ( t ) d t \forall x \in R,F(x) = \int_{-\infty}^{x} p(t)dt 性质:
非负性:
p ( x ) ≥ 0 p(x) \ge 0 正规性:
∫ − ∞ + ∞ p ( x ) d x = 1 \int_{-\infty}^{+\infty} p(x)dx = 1 可积性:
∀ x 1 ≤ x 2 , P ( x 1 ≤ X ≤ x 2 ) = F ( x 2 ) − F ( x 1 ) = ∫ x 1 x 2 p ( x ) d x \forall x_1 \le x_2,P(x_1 \le X \le x_2) = F(x_2) - F(x_1) = \int_{x_1}^{x_2}p(x)dx 分布函数可导性:若
p ( x ) p(x) x x F ′ ( x ) = p ( x ) F'(x) = p(x) 已知事件但无意义性:
∀ x ∈ R , P ( X = x ) = F ( x ) − F ( x ) = 0 \forall x \in R, P(X=x) = F(x) - F(x) = 0 - 离散型变量可以通过列举随机变量
X X P ( A ) = 0 P(A) = 0 A A P ( A ) = 1 P(A)=1 A A - 对于连续型随机变量
X X P ( x 1 < X < X 2 ) = P ( x 1 < X ≤ X 2 ) = P ( x 1 ≤ X < X 2 ) = P ( x 1 ≤ X ≤ X 2 ) P(x_1 < X < X_2)=P(x_1 < X \le X_2)=P(x_1 \le X < X_2)=P(x_1 \le X \le X_2)
- 离散型变量可以通过列举随机变量
实际描述性:密度函数的数值反映了随机变量
X X x x p ( x ) Δ x ≈ ∫ x x + Δ x p ( t ) d t = F ( x + Δ x ) − F ( x ) = P ( x ≤ X ≤ x + Δ x ) p(x)\Delta x \approx \int_{x}^{x+\Delta x} p(t)dt = F(x+\Delta x) - F(x) = P(x \le X \le x+\Delta x)
2.3.2 常用连续型随机变量及其密度函数
| 分布定义式 | 概率密度函数 | 分布函数 | |
|---|---|---|---|
| 均匀分布 | |||
| 指数分布 | |||
| 正态分布 |
补充说明:
指数分布:其中参数
λ > 0 \lambda >0 正态分布:一般正态函数
F ( x ) F(x) Φ ( x ) \Phi(x) F ( x ) = Φ ( x − μ σ ) F(x) = \Phi(\frac{x - \mu}{\sigma}) 于是对于计算一般正态函数的函数值,就可以通过下式将其转化为标准正态函数,最后查表即可:
2.4 随机变量函数的分布
本目主要介绍给定一个随机变量
2.4.1 离散型随机变量函数的分布
通过关系式
2.4.2 连续型随机变量函数的分布
给定随机变量
方法一:先求解随机变量
Y Y F Y ( y ) F_Y(y) p Y ( y ) p_Y(y) 即先
F Y ( y ) = P Y ( Y ≤ y ) = P Y ( g ( X ) ≤ y ) = P X ( X ≤ f ( y ) ) = F X ( f ( y ) ) F_Y(y) = P_Y(Y \le y) = P_Y(g(X) \le y) = P_X(X \le f(y)) = F_X(f(y)) Y Y 再对
F Y ( y ) F_Y(y) p Y ( y ) = d d y F Y ( y ) = d d y F X ( f ( y ) ) = F X ′ ( f ( y ) ) ⋅ f ′ ( y ) = p X ( f ( y ) ) ⋅ f ′ ( y ) \displaystyle p_Y(y) = \frac{d}{dy} F_Y(y) = \frac{d}{dy} F_X(f(y)) = F_X'(f(y)) \cdot f'(y) = p_X(f(y)) \cdot f'(y) 方法二:如果关系式
y = g ( x ) y=g(x) x = h ( y ) x=h(y) Y Y p Y ( y ) p_Y(y) α \alpha β \beta Y = g ( X ) Y=g(X) x x h ( y ) h(y) y y p Y ( y ) = { p X ( h ( y ) ) ⋅ ∣ h ′ ( y ) ∣ , α < y < β 0 , 其他 p_Y(y) = \begin{cases}p_X(h(y)) \cdot |h'(y)|, & \alpha < y < \beta \\0, & \text{其他}\end{cases}
第3章 随机向量及其分布
实际生活中,只采用一个随机变量描述事件往往是不够的。本章引入多维的随机变量概念,构成随机向量,从二维开始,推广到
3.1 二维随机向量的联合分布
现在我们讨论二维随机向量的联合分布。所谓的联合分布,其实就是一个曲面的概率密度(离散型就是点集),而分布函数就是对其积分得到的三维几何体的体积(散点和)而已。
3.1.1 联合分布函数
定义:我们定义满足下式的二元函数
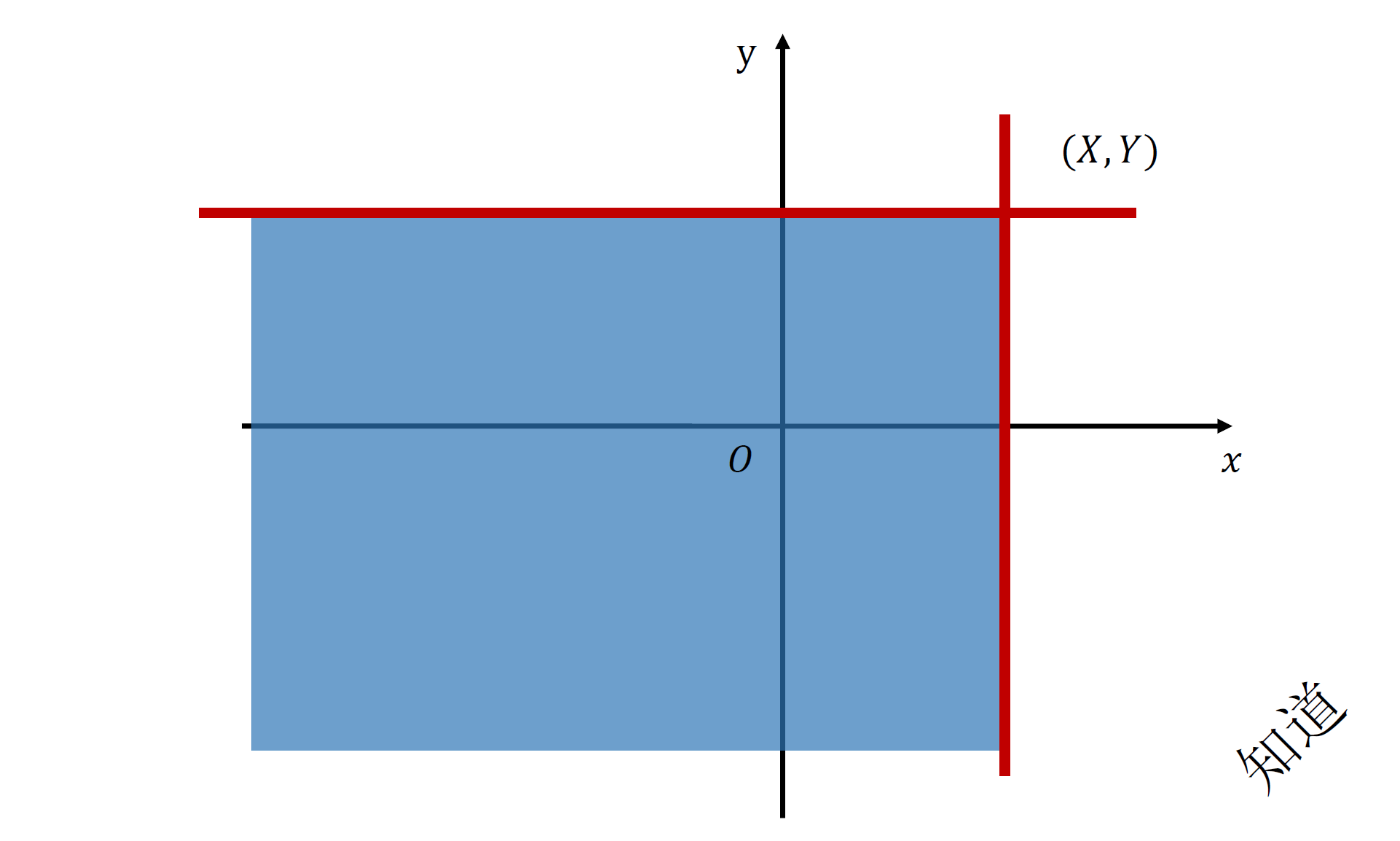
性质:其实配合几何意义理解就会很容易了
- 固定某一维度,另一维度是单调不减的
- 对于每个维度都是右连续的
- 固定某一维度,另一维度趋近于负无穷对应的函数值为
0 0 - 二维前缀和性质,右上角的矩阵面积
≥ 0 \ge 0
3.1.2 联合分布列
定义:若二维随机向量
表示:有两种表示二维随机向量分布列的方法,如下
公式法
p i j = P ( X = x i , Y = y i ) , i , j = 1 , 2 , ⋯ p_{ij} = P(X=x_i,Y = y_i), \quad i,j=1,2,\cdots 表格法:

性质:
- 非负性:
p i j ≥ 0 , i , j = 1 , 2 , ⋯ p_{ij} \ge 0, \quad i,j=1,2,\cdots - 正规性:
∑ i ∑ j p i j = 1 \displaystyle \sum_{i} \sum_{j} p_{ij} = 1
3.1.3 联合密度函数
定义:
性质:
- 非负性:
∀ x , y ∈ R , p ( x , y ) ≥ 0 \forall x,y \in R,p(x,y) \ge 0 - 正规性:
∫ − ∞ + ∞ ∫ − ∞ + ∞ p ( x , y ) d x d y = 1 \displaystyle \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} p(x,y)dxdy = 1
结论:
- 联合分布函数相比于一元分布函数,其实就是从概率密度函数与
x x x O y xOy - 若概率密度曲面在
x O y xOy
常见的连续型二维分布:
二维均匀分布:假设该曲面与
x O y xOy S S 1 S \frac{1}{S} p ( x , y ) = { 1 S , ( x , y ) ∈ G 0 , 其他 p(x,y) = \begin{cases}\frac{1}{S}, &(x,y) \in G \\0, &\text{其他}\end{cases} 二元正态分布:不要求掌握密度函数,可以感受一下密度函数的图像:
▶二元正态分布 - 密度函数的图像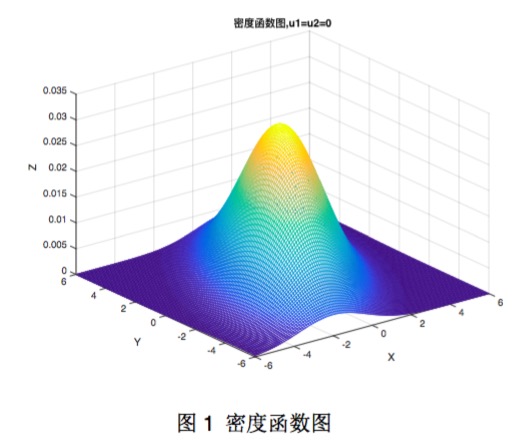
计算题:往往给出一个二元密度函数,然后让我们求解(1)密度函数中的参数、(2)分布函数、(3)联合事件某个区域下的概率
(1)我们利用二元密度函数的正规性,直接积分值为
(2)划分区间后进行曲面积分即可,在曲面积分时往往结合
(3)画出概率密度曲面在
3.2 二维随机向量的边缘分布
对于二元分布函数,我们也可以研究其中任意一个随机变量的分布情况,而不需要考虑另一个随机变量的取值情况。举一个实例就是,假如当前的随机向量是身高和体重,所谓的只研究其中一个随机变量,即边缘分布函数的情形就是,我们不考虑身高只考虑体重的分布情况;或者我们不考虑体重,只考虑身高的分布情况。接下来,我们将从边缘分布函数入手,逐渐学习离散型的分布列与连续型的分布函数。
3.2.1 边缘分布函数
我们称
3.2.2 边缘分布列
所谓的边缘分布列,就是固定一个随机变量,另外的随机变量取遍,组成的分布列。即:
我们称:
P ( X = x i ) P(X=x_i) ( X , Y ) (X,Y) X X P ( Y = y j ) P(Y=y_j) ( X , Y ) (X,Y) Y Y
3.2.3 边缘密度函数
所谓的的边缘密度函数,可以与边缘分布列进行类比,也就是固定一个随机变量,另外的随机变量取遍。只不过连续型的取遍就是无数个点,而离散型的取遍是可列个点,仅此而已。即:
我们称:
P ( X = x ) P(X=x) ( X , Y ) (X,Y) X X P ( Y = y ) P(Y=y) ( X , Y ) (X,Y) Y Y
3.3 随机向量的条件分布
本目主要介绍的是条件分布。所谓的条件分布,其实就是在约束一个随机变量为定值的情况下,另外一个随机变量的取值情况。与上述联合分布、边缘分布的区别在于:
- 联合分布、边缘分布的分布函数是一个体积(散点和),概率密度(分布列)是一个曲面(点集)
- 条件分布的分布函数是一个面积(散点和),概率密度(分布列)是一个曲线(点集)
3.3.1 离散型随机向量的条件分布列和条件分布函数
条件分布列,即散点情况:
我们称:
p i ∣ j p_{i|j} Y = y j Y=y_j X X p j ∣ i p_{j|i} X = x i X=x_i Y Y
条件分布函数,即点集情况:
我们称:
F ( x ∣ y j ) F(x|y_j) Y = y j Y=y_j X X F ( y ∣ x i ) F(y|x_i) X = x i X=x_i Y Y
3.3.2 连续型随机向量的条件密度函数和条件分布函数
条件密度函数,即联合分布的概率密度曲面上,约束了某一维度的随机变量为定值,于是条件密度函数的图像就是一个空间曲线:
我们称:
p ( x ∣ y ) p(x|y) Y = y Y=y X X p ( y ∣ x ) p(y|x) X = x X=x Y Y
条件分布函数,即上述曲线的分段积分结果:
我们称:
F ( x ∣ y ) F(x|y) Y = y Y=y X X F ( y ∣ x ) F(y|x) X = x X=x Y Y
3.4 随机变量的独立性
本目主要介绍随机变量的独立性。我们知道随机事件之间是有独立性的,即满足
定义:我们定义如果两个随机变量的分布函数满足下式,则两个随机变量相互独立:
F ( x , y ) = F X ( x ) F Y ( y ) F(x,y)=F_X(x)F_Y(y) 性质:对于随机向量
( X , Y ) (X,Y) 随机变量
X X Y Y 离散型: P ( X = x i , Y = y j ) = P ( X = x i ) P ( Y = y j ) 连续型: p ( x , y ) = p X ( x ) p Y ( y ) \begin{aligned}\text{离散型:}& P(X=x_i,Y=y_j) = P(X=x_i)P(Y=y_j) \\\text{连续型:}& p(x,y) = p_X(x)p_Y(y)\end{aligned} 若随机变量
X X Y Y h ( ⋅ ) h(\cdot) g ( ⋅ ) g(\cdot) h ( X ) , g ( Y ) h(X),g(Y)
3.5 随机向量函数的分布
在 2.4 目中我们了解到了随机变量函数的分布,现在我们讨论随机向量函数的分布。在生活中,假设我们已经知道了一个人群中所有人的身高和体重的分布情况,现在想要血糖根据身高和体重的分布情况,就需要用到本目的理念。我们从离散型和连续型随机向量
3.5.1 离散型随机向量函数的分布
按照规则枚举即可。
3.5.2 连续型随机向量函数的分布
与连续型随机变量函数的分布类似,这类题目一般也是:给定随机向量
(1) 和的分布:
先求分布函数
F Z ( z ) F_Z(z) F Z ( z ) = P ( X + Y ≤ z ) = ∬ x + y ≤ z p ( x , y ) d x d y = ∫ − ∞ z [ ∫ − ∞ + ∞ p ( x , t − x ) d x ] d t = ∫ − ∞ z [ ∫ − ∞ + ∞ p ( t − y , y ) d y ] d t \begin{aligned}F_Z(z) &= P(X+Y \le z) \\&= \iint\limits_{x+y \le z} p(x,y) dxdy \\&\begin{align}&= \int _{-\infty}^z \left [ \int_{-\infty}^{+\infty} p(x,t-x)dx \right ] dt \\&= \int _{-\infty}^z \left [ \int_{-\infty}^{+\infty} p(t-y,y)dy \right ] dt\end{align}\end{aligned} 由分布函数定义:
F X ( x ) = ∫ − ∞ x p ( u ) d u F_X(x) = \int_{-\infty}^xp(u)du 所以可得
Z = X + Y Z=X+Y p Z ( z ) p_Z(z) p Z ( z ) = ∫ − ∞ + ∞ p ( x , z − x ) d x ( 1 ) p Z ( z ) = ∫ − ∞ + ∞ p ( z − y , y ) d y ( 2 ) \begin{aligned}p_Z(z) = \int_{-\infty}^{+\infty} p(x,z-x)dx \quad &(1) \\p_Z(z) = \int_{-\infty}^{+\infty} p(z-y,y)dy \quad &(2) \\\end{aligned} 若 X 和 Y 相互独立,还可得卷积式:
p Z ( z ) = ∫ − ∞ + ∞ p ( x , z − x ) d x = ∫ − ∞ + ∞ p X ( x ) ⋅ p Y ( z − x ) d x ( 1 ) p Z ( z ) = ∫ − ∞ + ∞ p ( z − y , y ) d y = ∫ − ∞ + ∞ p X ( z − y ) ⋅ p Y ( y ) d y ( 2 ) \begin{aligned}p_Z(z) &= \int_{-\infty}^{+\infty} p(x,z-x)dx \\&= \int_{-\infty}^{+\infty} p_X(x)\cdot p_Y(z-x) dx \quad &(1) \\p_Z(z) &= \int_{-\infty}^{+\infty} p(z-y,y)dy \\&= \int_{-\infty}^{+\infty} p_X(z-y)\cdot p_Y(y) dy \quad &(2)\end{aligned}
(2) 次序统计量的分布(对于两个相互独立的随机变量 X 和 Y):
对于
M = max ( X , Y ) M=\max{(X,Y)} F M ( z ) = P ( M ≤ z ) = P ( max ( X , Y ) ≤ z ) = P ( X ≤ z , Y ≤ z ) = P ( X ≤ z ) ⋅ P ( Y ≤ z ) = F X ( z ) ⋅ F Y ( z ) \begin{aligned}F_M(z) &= P(M \le z) \\&= P(\max{(X,Y)} \le z) \\&= P(X \le z, Y \le z) \\&= P(X \le z) \cdot P(Y \le z) \\&= F_X(z) \cdot F_Y(z)\end{aligned} 对于
N = min ( X , Y ) N=\min{(X,Y)} F N ( z ) = P ( N ≤ z ) = P ( min ( X , Y ) ≤ z ) = 1 − P ( min ( X + Y ) ≥ z ) = 1 − P ( X ≥ z , Y ≥ z ) = 1 − P ( X ≥ z ) ⋅ P ( Y ≥ z ) = 1 − [ 1 − F X ( z ) ] ⋅ [ 1 − F Y ( z ) ] \begin{aligned}F_N(z) &= P(N \le z) \\&= P(\min{(X,Y)} \le z) \\&= 1 - P(\min{(X+Y)} \ge z) \\&= 1 - P(X \ge z,Y \ge z) \\&= 1 - P(X \ge z) \cdot P(Y \ge z) \\&= 1 - [1 - F_X(z)] \cdot [1 - F_Y(z)]\end{aligned} 若拓展到
n n F M ( z ) = [ F ( z ) ] n p M ( z ) = n p ( z ) [ F ( z ) ] n − 1 \begin{aligned}F_M(z) &= [F(z)]^n \\p_M(z) &= np(z)[F(z)]^{n-1}\end{aligned} F N ( z ) = 1 − [ 1 − F ( z ) ] n p N ( z ) = n p ( z ) [ 1 − F ( z ) ] n − 1 \begin{aligned}F_N(z) &= 1 - [1-F(z)]^n \\p_N(z) &= np(z)[1-F(z)]^{n-1}\end{aligned}
第4章 随机变量的数字特征
本章我们将学习随机变量的一些数字特征。所谓的数字特征其实就是随机变量分布的一些内在属性,比如均值、方差、协方差等等,有些分布特性甚至可以通过某个数字特征而直接觉得。其中期望和方差往往用来衡量单个随机变量的特征,而协方差与相关系数则是用来衡量随机变量之间的数字特征。接下来开始介绍。
4.1 数学期望
加权平均概念的严格数学定义。
4.1.1 随机变量的数学期望
离散型
E X = ∑ i = 1 ∞ x i p i EX = \sum_{i=1}^{\infty} x_i p_i 连续型
E X = ∫ − ∞ + ∞ x p ( x ) d x \begin{aligned}&EX = \int_{-\infty}^{+\infty} xp(x)dx\end{aligned}
4.1.2 随机变量函数的数学期望
离散型
一元
E g ( X ) = ∑ i = 1 ∞ g ( x i ) p i Eg(X) = \sum_{i=1}^{\infty}g(x_i)p_i 二元
E g ( X , Y ) = ∑ i = 1 ∞ ∑ j = 1 ∞ g ( x i , y i ) p i j Eg(X,Y) = \sum_{i=1}^{\infty}\sum_{j=1}^{\infty}g(x_i,y_i)p_{ij}
连续型
一元
E g ( X ) = ∫ − ∞ + ∞ g ( x ) p ( x ) d x Eg(X) = \int_{-\infty}^{+\infty}g(x)p(x)dx 二元
E g ( X , Y ) = ∫ − ∞ + ∞ ∫ − ∞ + ∞ g ( x i , y i ) p ( x , y ) d x d y Eg(X,Y) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x_i,y_i)p(x,y)dxdy
4.1.3 数学期望的性质
E C = C EC=C E ( C X ) = C E X E(CX)=CEX E ( X + Y ) = E X + E Y E(X+Y)=EX+EY - 若
X X Y Y E ( X Y ) = E X E Y E(XY)=EXEY
4.2 方差
随机变量的取值与均值之间的离散程度。
4.2.1 方差的定义
我们定义随机变量
4.2.2 方差的性质
下列方差的性质全部可由上述方差的定义式,结合期望的性质推导而来:
D ( a X + b ) = a 2 D ( X ) D(aX+b) = a^2D(X) 若
X 1 , X 2 , ⋯ X_1,X_2,\cdots D ( a X 1 ± b X 2 ± ⋯ ) = a 2 D ( X 1 ) + b 2 D ( X 2 ) + ⋯ D(aX_1 \pm bX_2 \pm \cdots) = a^2D(X_1) + b^2D(X_2) + \cdots E [ ( X − E X ) 2 ] ≤ E [ ( X − C ) 2 ] E\left[ (X-EX)^2 \right] \le E \left [ (X-C)^2 \right ] 切比雪夫不等式
(本以为不要求掌握的,但是被小测拷打了,补一下):∀ ϵ > 0 , P ( ∣ X − E X ∣ < ϵ ) ≥ 1 − D X ϵ 2 \forall \epsilon >0, P(|X - EX| < \epsilon) \ge 1 - \frac{DX}{\epsilon^2}
4.3 结论与推导(补)
| 类型 | 分布 | 符号 | 期望 | 方差 |
|---|---|---|---|---|
| 离散型 | 0-1 分布 | |||
| — | *二项分布 | |||
| — | 几何分布 | |||
| — | *泊松分布 | |||
| 连续型 | 均匀分布 | |||
| — | 指数分布 | |||
| — | *正态分布 |
注:打星号表示在两个随机变量
X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) → X ± Y ∼ N ( μ 1 ± μ 2 , σ 1 2 + σ 2 2 ) X \sim N(\mu_1,\sigma_1^2), Y \sim N(\mu_2,\sigma_2^2) \to X\pm Y\sim N(\mu_1\pm\mu_2,\sigma_1^2+\sigma_2^2) X ∼ B ( n 1 , p ) , Y ∼ B ( n 2 , p ) → X + Y ∼ B ( n 1 + n 2 , p ) X \sim B(n_1,p), Y \sim B(n_2,p) \to X+Y\sim B(n_1+n_2,p) X ∼ P ( λ 1 ) , Y ∼ P ( λ 2 ) → X + Y ∼ P ( λ 1 + λ 2 ) X \sim P(\lambda_1),Y\sim P(\lambda_2) \to X+Y \sim P(\lambda_1+\lambda_2)
推导的根本方式还是从定义出发。当然为了省事也可以从性质出发。
0-1 分布
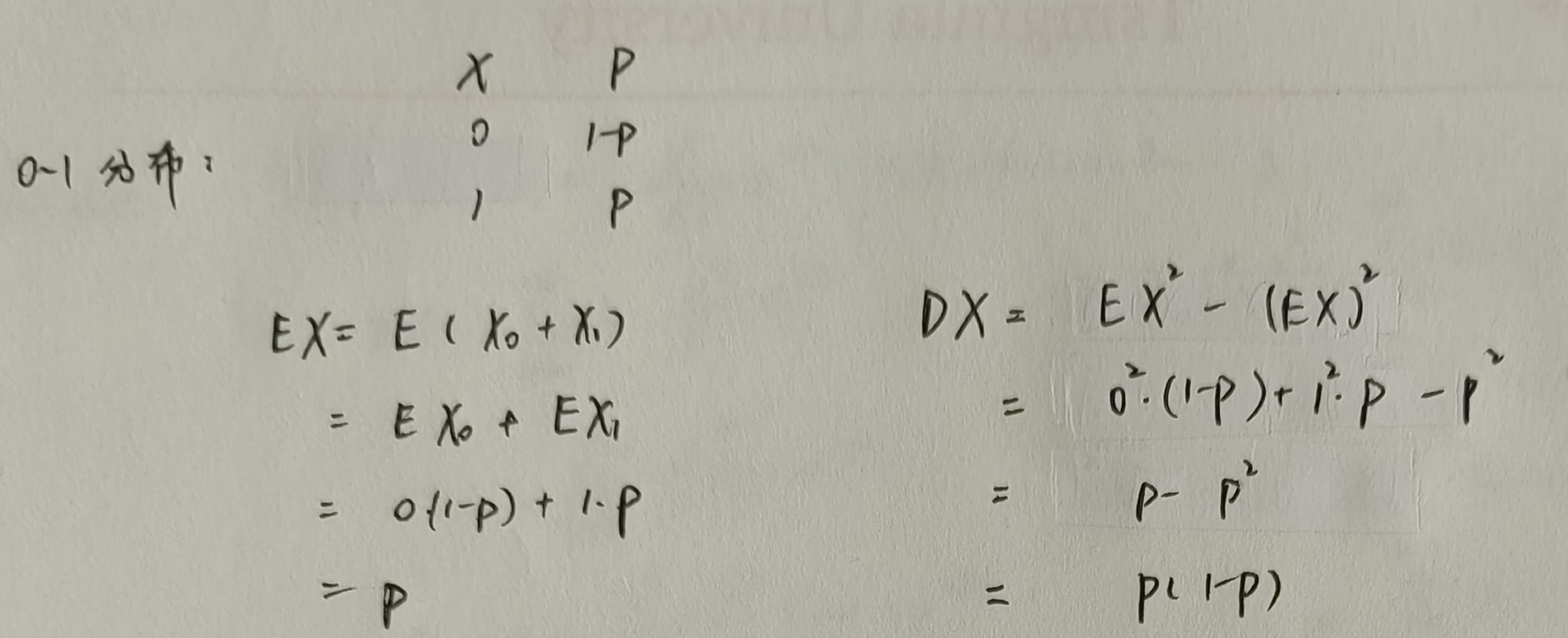
二项分布
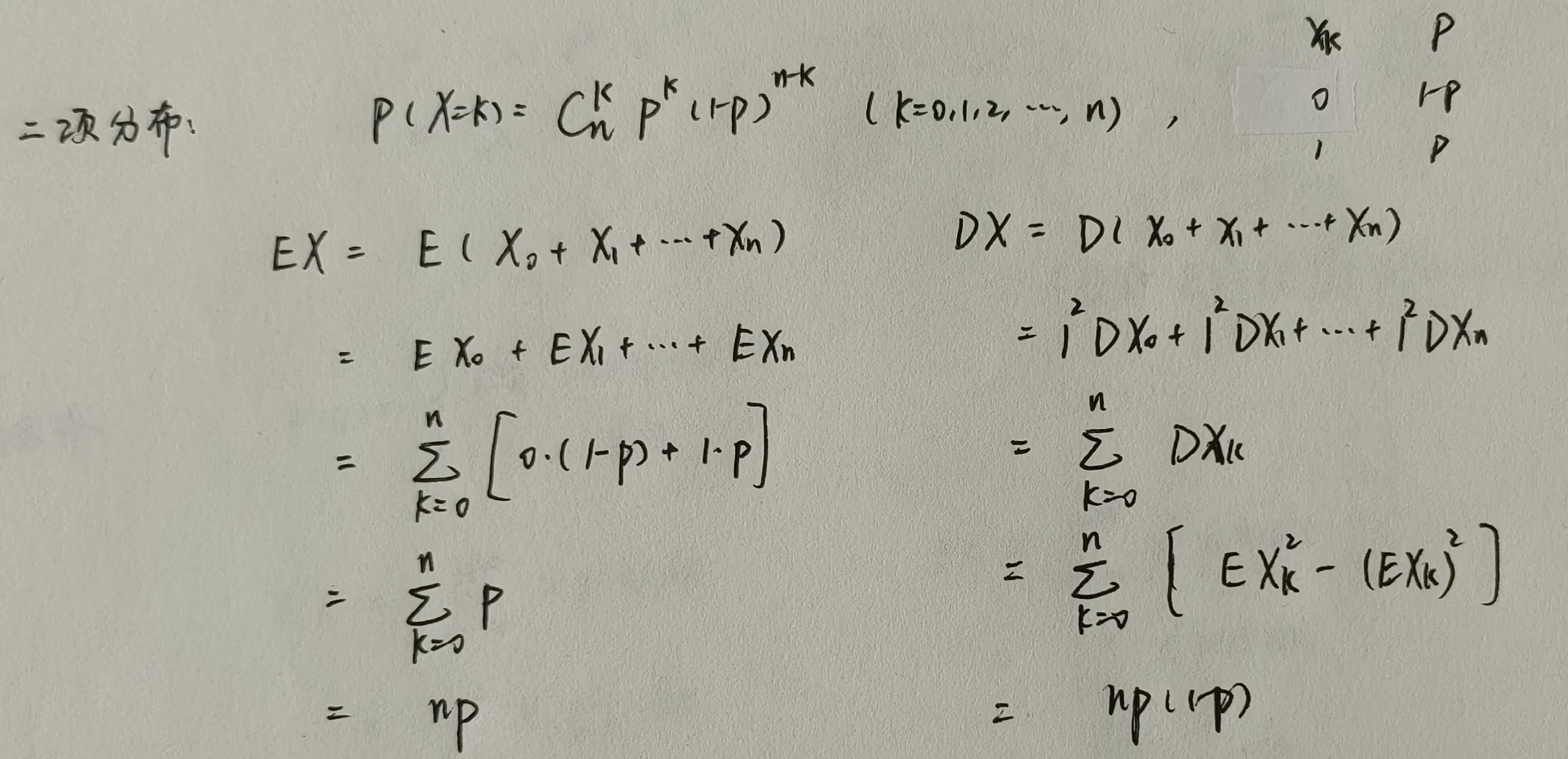
几何分布
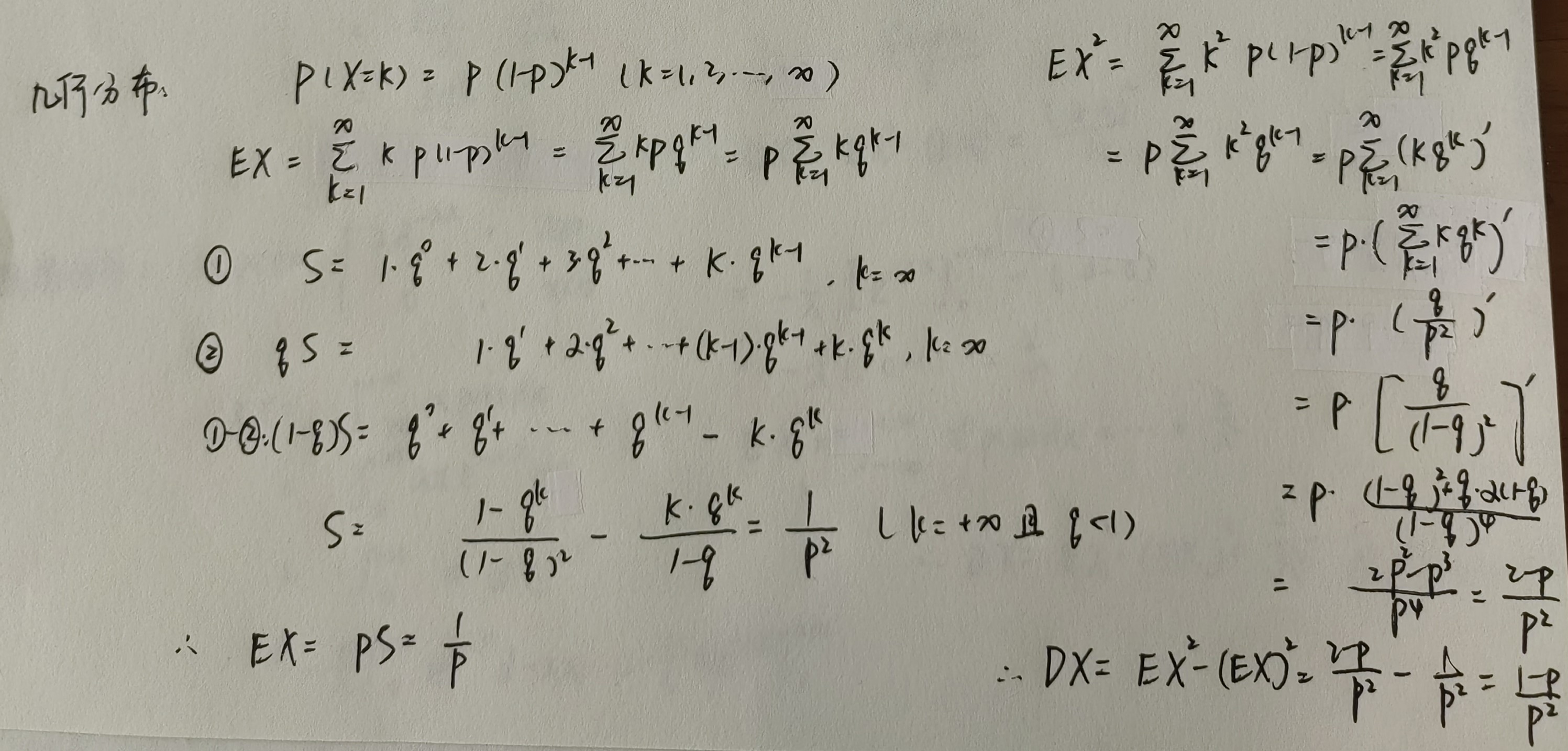
泊松分布
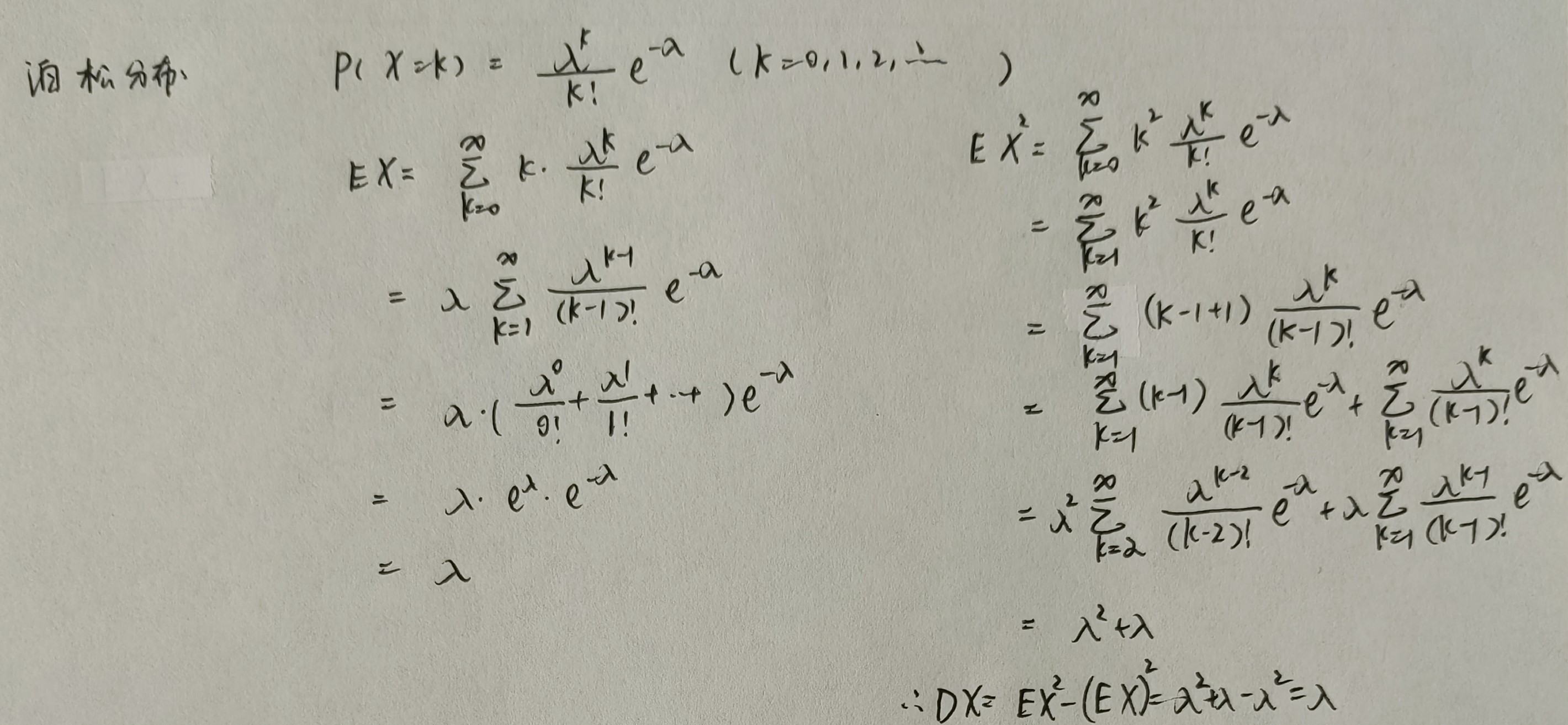
均匀分布
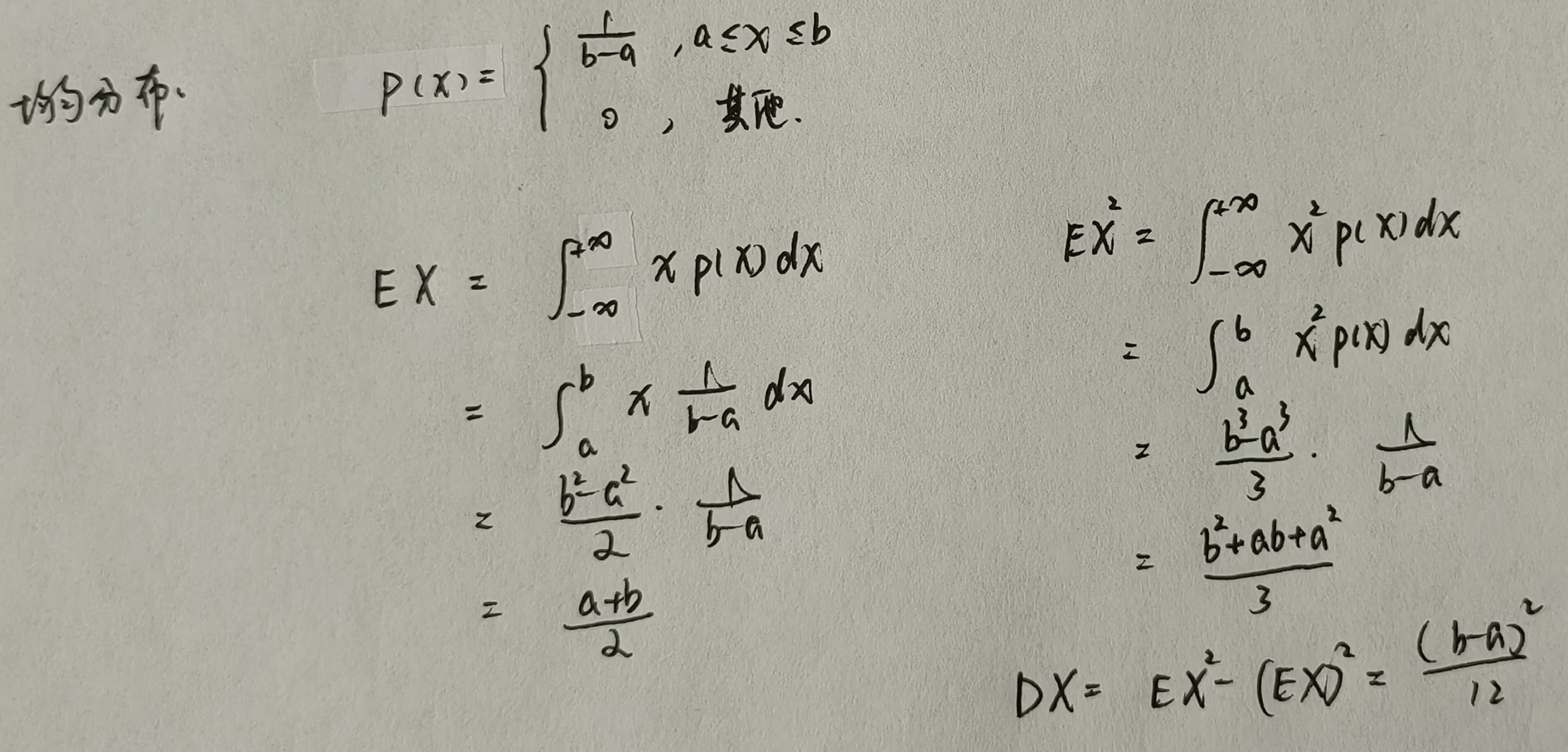
指数分布
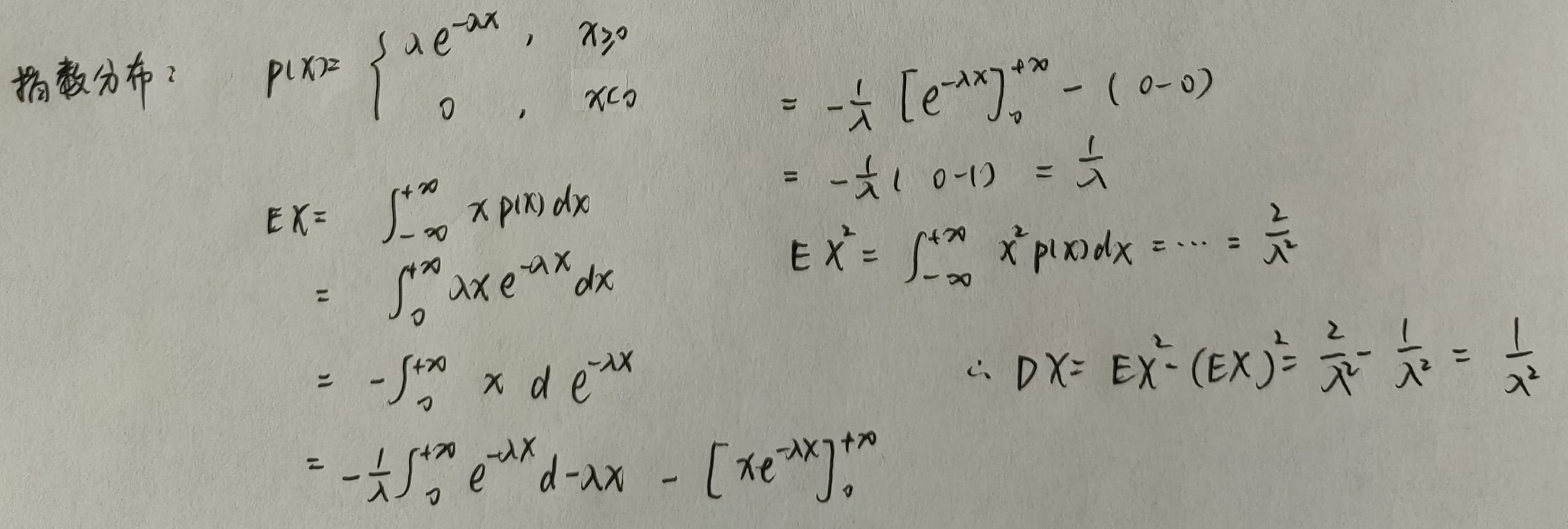
4.4 协方差与相关系数
4.4.1 协方差
定义:随机变量 X 与 Y 的协方差
特别的:
性质:
- 交换律:
C o v ( X , Y ) = C o v ( Y , X ) Cov(X,Y)=Cov(Y,X) - 提取率:
C o v ( a X , b Y ) = a b C o v ( X , Y ) Cov(aX,bY)=abCov(X,Y) - 分配率:
C o v ( X 1 + X 2 , Y ) = C o v ( X 1 , Y ) + C o v ( X 2 , Y ) Cov(X_1+X_2,Y) = Cov(X_1,Y)+Cov(X_2,Y) - 独立性:若 X 与 Y 相互独立,则
C o v ( X , Y ) = 0 Cov(X,Y)=0 - 放缩性:
[ C o v ( X , Y ) ] 2 ≤ D X ⋅ D Y \left[Cov(X,Y)\right]^2 \le DX \cdot DY
4.4.2 相关系数
定义:相关系数
特别的:
- 若
0 < ρ < 1 0 < \rho < 1 - 若
− 1 < ρ < 0 -1<\rho<0
性质:
- 放缩性(由协方差性质5可得):
∣ ρ ∣ ≤ 1 |\rho| \le 1 - 独立性(由协方差性质4可得):若 X 与 Y 相互独立,则
p = 0 p=0 - 线性相关性(不予证明):
∣ ρ ∣ = 1 |\rho|=1 a ( a ≠ 0 ) , b a(a\ne0),b P ( Y = a X + b ) = 1 P(Y=aX+b)=1
4.4.3 独立性与线性相关性(补)
一般的:对于两个随机变量
X X Y Y → \rightarrow X X Y Y X X Y Y ↚ \nleftarrow X X Y Y X X Y Y
特别的:对于满足二维正态分布的随机变量
X X Y Y → \rightarrow X X Y Y X X Y Y ← \leftarrow X X Y Y
第5章 大数定律与中心极限定理
本章只需要知道一个独立同分布中心极限定理即可,至于棣莫弗-拉普拉斯中心极限定理其实就是前者的
独立同分布中心极限定理
定义:
解释:其实就是对于独立同分布的随机事件
第6章 数理统计的基本概念
开始统计学之旅。
6.1 总体与样本
类比 ML:数据集=总体,样本=样本。
我们只研究一种样本:简单随机样本
( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n)
同样的,我们研究总体
分布:由于样本相互独立,故:
F ( x 1 , x 2 , . . . , x n ) = F ( x 1 ) F ( x 2 ) ⋯ F ( x n ) F(x_1,x_2,...,x_n)=F(x_1)F(x_2) \cdots F(x_n) 联合密度:同样由于样本相互独立,故:
p ( x 1 , x 2 , . . . , x n ) = p ( x 1 ) p ( x 2 ) ⋯ p ( x n ) p(x_1,x_2,...,x_n)=p(x_1)p(x_2) \cdots p(x_n)
6.2 经验分布与频率直方图
经验分布函数是利用样本得到的。也是给区间然后统计样本频度进而计算频率,只不过区间长度不是固定的。
频率直方图就是选定固定的区间长度,然后统计频度进而计算频率作图。
6.3 统计量
统计量定义:关于样本不含未知数的表达式。
常见统计量:假设
一、样本均值和样本方差
样本均值:
X ‾ = 1 n ∑ i = 1 n X i \displaystyle \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i 样本方差:
S 0 2 = 1 n ∑ i = 1 n ( X i − X ‾ ) 2 = 1 n ∑ i = 1 n X i 2 − X ‾ 2 \displaystyle S_0^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 = \frac{1}{n}\sum_{i=1}^n X_i^2 - \overline{X}^2 样本标准差:
S 0 = S 0 2 \displaystyle S_0 = \sqrt{S_0^2} 修正样本方差:
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 \displaystyle S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X})^2 修正样本标准差:
S = S 2 \displaystyle S = \sqrt{S^2} ▶推导设总体
X X μ \mu σ 2 \sigma^2 ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) 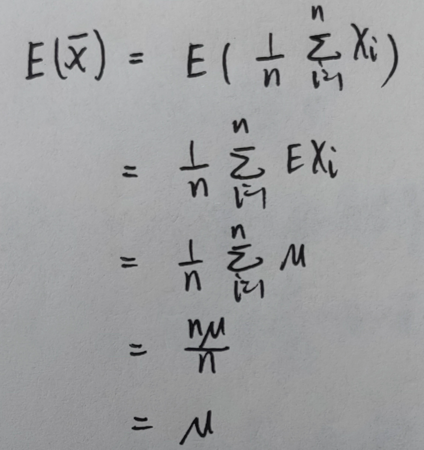
即:样本均值的数学期望
= = 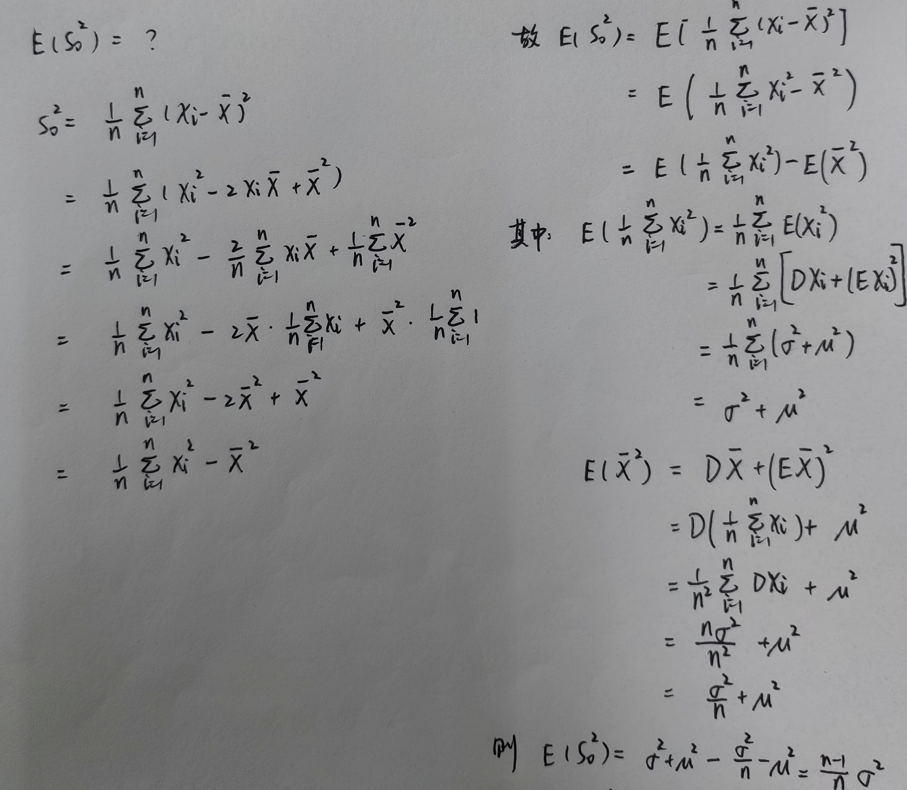
即:样本方差的数学期望
≠ \ne 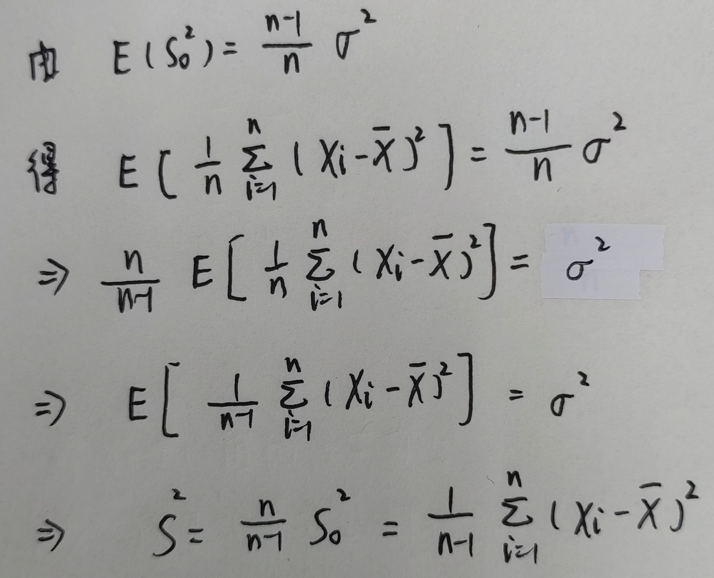
上图即:修正样本方差推导
样本
k k A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , ⋯ \displaystyle A_k = \frac{1}{n} \sum_{i=1}^n X_i^k,\quad k=1,2,\cdots 样本
k k B k = 1 n ∑ i = 1 n ( X i − X ‾ ) k , k = 2 , 3 , ⋯ \displaystyle B_k = \frac{1}{n} \sum_{i=1}^n (X_i-\overline{X})^k,\quad k=2,3,\cdots
二、次序统计量
- 序列最小值
- 序列最大值
- 极差 = 序列最大值 - 序列最小值
6.4 正态总体抽样分布定理
时刻牢记一句话:构造性定义!
6.4.1 卡方分布、t 分布、F 分布
分位数
- 我们定义实数
λ α \lambda_\alpha X X α \alpha P ( X > λ α ) = α P(X > \lambda_\alpha) = \alpha - 我们定义实数
λ 1 − β \lambda_{1-\beta} X X β \beta P ( X < λ 1 − β ) = β P(X < \lambda_{1-\beta})=\beta
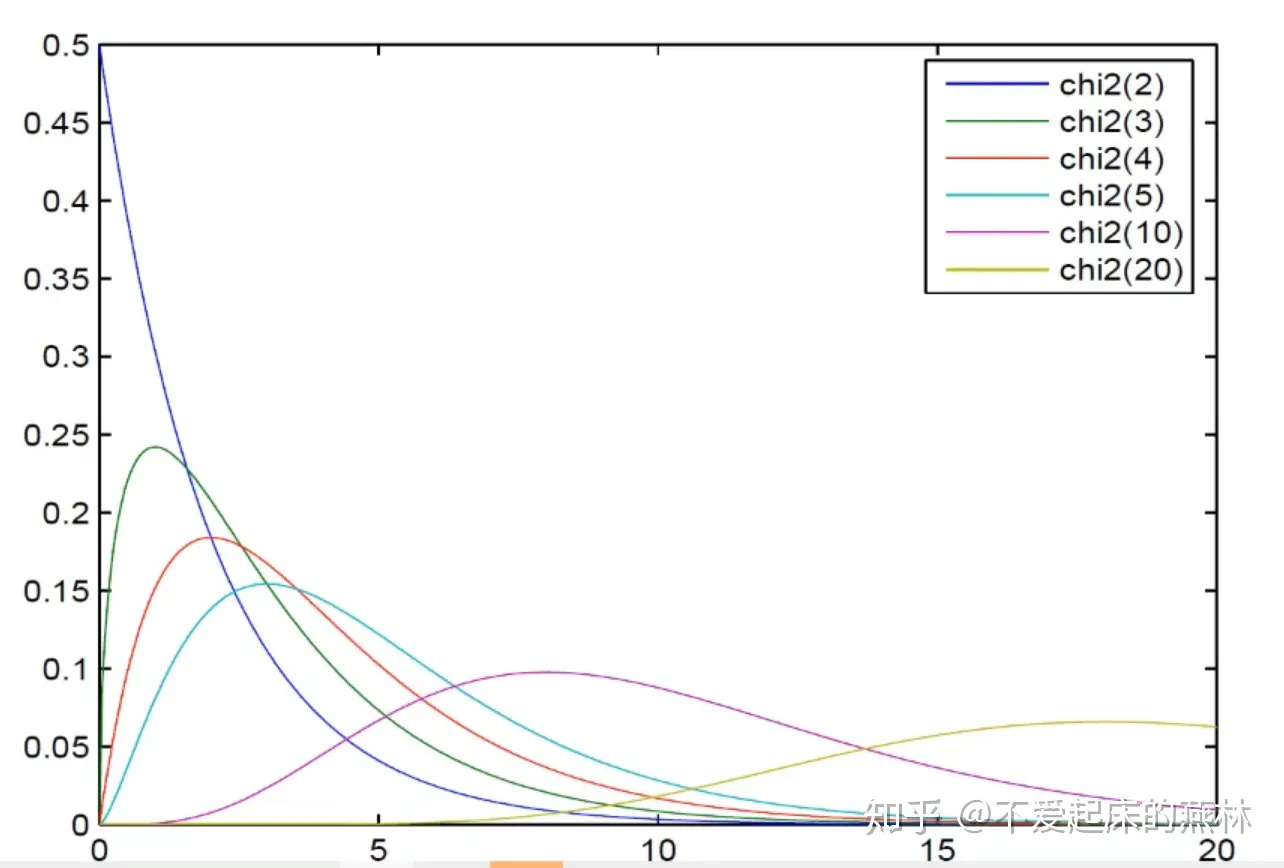
定义:
- 对于
n n X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots ,X_n Y = X 1 2 + X 2 2 + ⋯ + X n 2 Y = X_1^2 + X_2^2 + \cdots + X_n^2 - 则
Y Y n n χ 2 \chi^2 Y ∼ χ 2 ( n ) Y \sim \chi^2(n)
性质:
可加性:若
Y 1 ∼ χ 2 ( n 1 ) , Y 2 ∼ χ 2 ( n 2 ) Y_1 \sim \chi^2(n_1), Y_2 \sim \chi^2(n_2) Y 1 , Y 2 Y_1,Y_2 Y 1 + Y 2 ∼ χ 2 ( n 1 + n 2 ) Y_1+Y_2 \sim \chi^2(n_1+n_2) 统计性:对于
Y ∼ χ 2 ( n ) Y \sim \chi^2(n) E Y = n , D Y = 2 n EY = n, DY = 2n ▶推导EY 的推导利用:
E X 2 = D X − ( E X ) 2 EX^2 = DX - (EX)^2 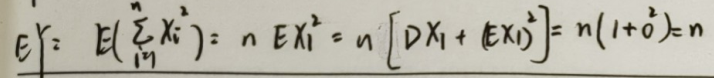
DY 的推导利用:方差计算公式、随机变量函数的数学期望进行计算
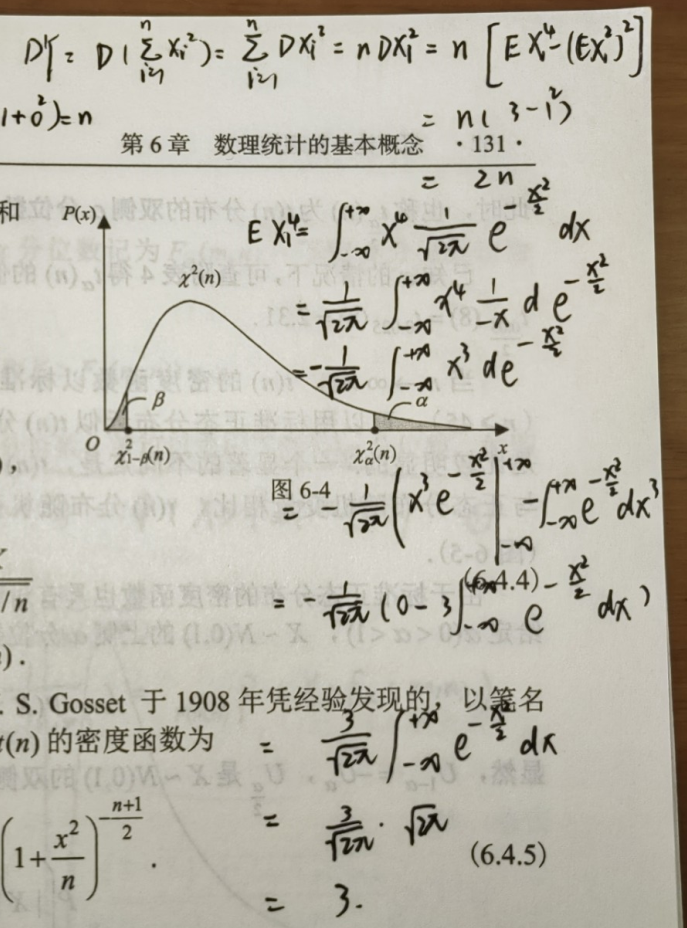
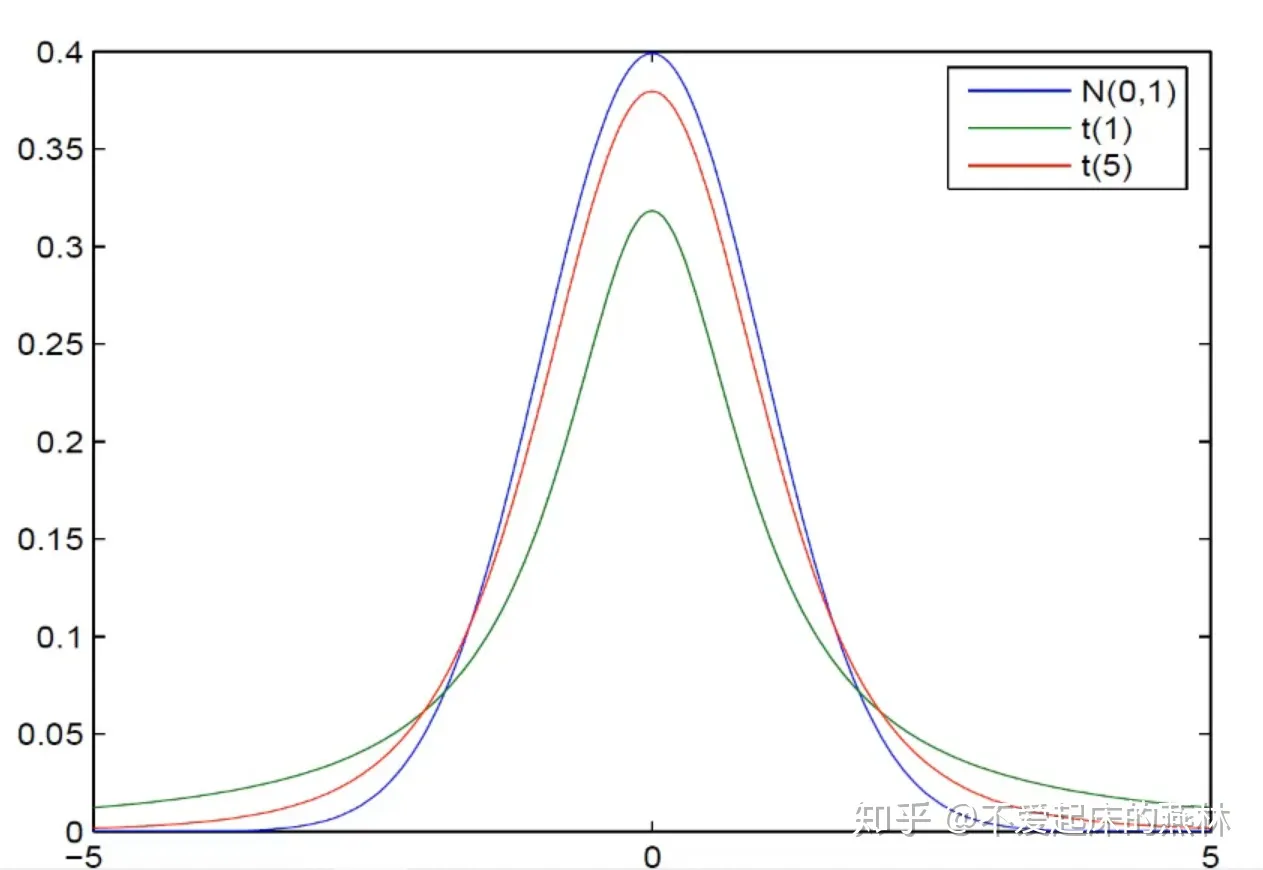
定义:
- 若随机变量
X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0, 1),Y \sim \chi^2 (n) X , Y X,Y - 则称随机变量
T = X Y / n T = \displaystyle \frac{X}{\sqrt{Y/n}} n n t t T ∼ t ( n ) T \sim t(n)
性质:
- 密度函数是偶函数,具备对称性
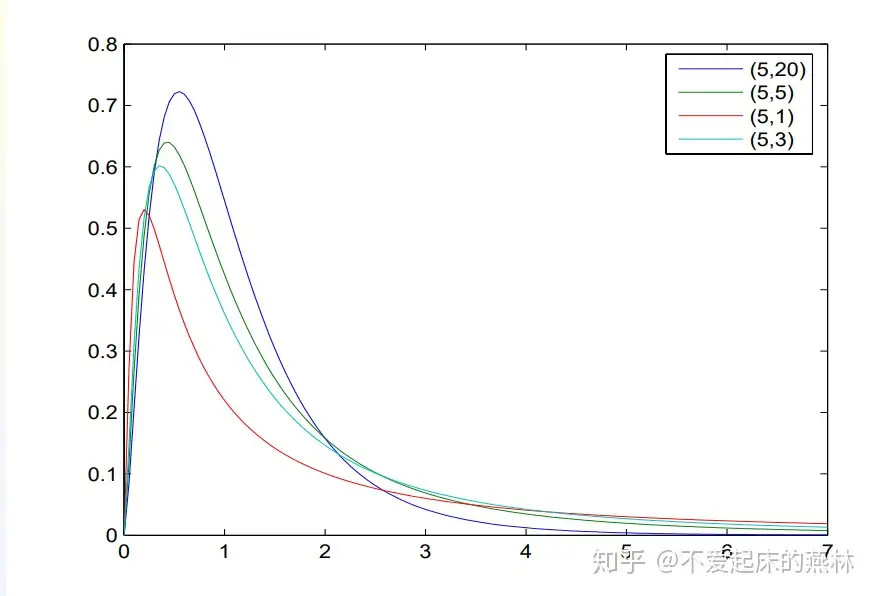
定义:
- 若随机变量
X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) - 则称随机变量
G = X / m Y / n G=\displaystyle \frac{X/m}{Y/n} ( m , n ) (m,n) F F G ∼ F ( m , n ) G \sim F(m, n)
性质:
- 倒数自由度转换:
1 G ∼ F ( n , m ) \displaystyle \frac{1}{G} \sim F(n, m) - 三变性质:
F 1 − α ( m , n ) = [ F α ( n , m ) ] − 1 \displaystyle F_{1-\alpha}(m, n) = \left [F_\alpha (n, m)\right]^{-1}
6.4.2 正态总体抽样分布基本定理
设
定理:
X ‾ ∼ N ( μ , σ 2 n ) \displaystyle \overline{X} \sim N(\mu, \frac{\sigma^2}{n}) ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \displaystyle \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) X ‾ \overline{X} S 2 S^2
推论:
n ( X ‾ − μ ) S ∼ t ( n − 1 ) \displaystyle \frac{\sqrt{n}(\overline{X} - \mu)}{S} \sim t(n-1)
第7章 参数估计
有些时候我们知道数据的分布类型,但是不清楚表达式中的某些参数,这就需要我们利用「已有的样本」对分布表达式中的参数进行估计。本章我们将从点估计、估计评价、区间估计三部分出发进行介绍。
7.1 点估计
所谓点估计策略,就是直接给出参数的一个估计值。本目我们介绍点估计策略中的两个方法:矩估计法、极大似然估计法。
7.1.1 矩估计法
其实就一句话:我们用样本的原点矩
7.1.2 极大似然估计法
基本原理是:在当前样本数据的局面下,我们希望找到合适的参数使得当前的样本分布情况发生的概率最大。由于各样本相互独立,因此我们可以用连乘的概率公式来计算当前局面的概率值:
上述
- 写出似然函数
L ( θ ) L(\theta) - 将上述似然函数取对数
- 求对数似然函数关于所有未知参数的偏导并计算极值点
- 解出参数关于样本统计量的表达式
离散型随机变量的似然函数表达式
连续型随机变量的似然函数表达式
可以看出极大似然估计本质上就是一个多元函数求极值的问题。特别地,当我们没法得到参数关于样本统计量的表达式
7.2 估计量的评价标准
如何衡量不同的点估计方法好坏?我们引入三种点估计量的评价指标:无偏性、有效性、一致性。其中一致性一笔带过,不做详细讨论。补充一点,参数的估计量
7.2.1 无偏性
顾名思义,就是希望估计出来的参数量尽可能不偏离真实值。我们定义满足下式的估计量
7.2.2 有效性
有效性是基于比较的定义方法。对于两个无偏估计
7.2.3 一致性
即当样本容量 n 趋近于无穷时,参数的估计值也能趋近于真实值,则称该估计量
7.3 区间估计
由于点估计只能进行比较,无法对单一估计进行性能度量。因此引入「主元法」的概念与「区间估计」策略
7.3.1 基本概念
可靠程度:参数估计区间越长,可靠程度越高
精确程度:参数估计区间越短,可靠程度越高
7.3.2 区间估计常用方法之主元法
主元法的核心逻辑就一个:在已知数据总体分布的情况下,构造一个关于样本
7.3.3 正态总体的区间估计
我们只需要掌握「一个总体服从正态分布」的情况。这种情况下的区间估计分为三种,其中估计均值
- 构造主元
Z ( X , θ ) Z(X,\theta) - 利用置信度
1 − α 1-\alpha Z Z - 对主元
Z Z θ \theta
为了提升区间估计的可信度,我们希望上述第 2 步计算出来的关于主元的取值范围尽可能准确。我们不加证明的给出以下结论:取主元的取值范围为 主元服从的分布的上下
(一) 求
构造主元
利用置信度
对主元
(二) 求
构造主元
利用置信度
对主元
(三) 求
构造主元
利用置信度
对主元
第8章 假设检验
第 7 章的参数估计是在总体分布已知且未知分布表达式中某些参数的情况下,基于「抽取的少量样本」进行的参数估计。
现在的局面同样,我们已知总体分布和不完整的分布表达式参数。现在需要我们利用抽取的少量样本判断样本所在向量空间是否符合某种性质。本章的「假设检验」策略就是为了解决上述情况而诞生的。我们主要讨论单个正态总体的情况并针对均值和方差两个参数进行假设和检验:
- 假设均值满足某种趋势,利用已知数据判断假设是否成立
- 假设方差满足某种趋势,利用已知数据判断假设是否成立
8.1 假设检验的基本概念
基本思想:首先做出假设并构造一个关于样本观察值和已知参数的检验统计量,接着计算假设发生的情况下小概率事件发生时该检验统计量的取值范围(拒绝域),最终代入已知样本数据判断计算结果是否在拒绝域内。如果在,则说明在当前假设的情况下小概率事件发生了,对应的假设为假;反之说明假设为真。
为了量化「小概率事件发生」这个指标,我们引入显著性水平
基于数据的实验导致我们无法避免错误,因此我们定义以下两类错误:
- 第一类错误:弃真错误。即假设正确,但由于数据采样不合理导致拒绝了真实的假设
- 第二类错误:存伪错误。即假设错误,同样因为数据的不合理导致接受了错误的假设
8.2 单个正态总体均值的假设检验
设
当总体方差
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
当总体方差
注:之所以这样构造是因为当总体
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
8.3 单个正态总体方差的假设检验
设
我们直接构造样本统计量
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
前言
学科情况:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 周效尧 | 4 | 学科基础课 |
成绩组成:
| 平时 | 测验(×2) | 期末 |
|---|---|---|
| 10% | 30% | 60% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 概率论与数理统计Ⅰ | 《概率论与数理统计》 | 第一版 | 刘国祥王晓谦 等主编 | 科学出版社 | 978-7-03-038317-4 |
学习资源:
- 📺 视频资源:《概率论与数理统计》教学视频全集(宋浩)
- 📖 教材答案:
- 本地路径(自用):[概率论答案.pdf](D:\华为云盘\2. Score\4. 概率论与数理统计\概率论答案.pdf)
- 网盘资源(共享):提取码:448w
第1章 事件与概率
1.1 随机事件与样本空间
1.1.1 样本空间
随机事件发生的总集合
1.1.2 随机事件
事件是否发生取决于观察结果的事件
1.1.3 事件之间的关系与运算
- 包含:
A ⊂ B A \subset B B ⊂ A B \subset A - 相等:
A = B A=B - 并(和):
A ∪ B A \cup B - 交(积):
A ∩ B ( A B ) A \cap B \quad (AB) - 互斥(互不相容):
A B = Φ AB=\Phi - 对立事件(余事件):
A ∩ B = Φ ∧ A ∪ B = Ω A \cap B=\Phi \land A \cup B=\Omega - 差:
A − B = A ∩ B ‾ = A B ‾ A-B=A \cap \overline{B} = A \overline B - 德摩根律
将事件发生的概率论转化为集合论进行计算与分析
1.2 概率的三种定义及其性质
1.2.1 概率的统计定义
从频率出发得到。
1.2.2 概率的古典定义
特征:
- 样本空间是有限集
- 等可能性(试验中每个基本事件发生的概率是等可能的)
内容:
- 模型与计算公式
- 基本组合分析公式
- 乘法、加法原理
- 排列公式
- 组合公式
- 实例
- 超几何概率
- 分房问题
- 生日问题
- 古典概率的基本性质
1.2.3 概率的几何定义
特征:
- 样本空间不可列
- 等可能性
内容:
- 模型与计算公式
- 实例
- 一维几何图形:公交车乘车问题
- 二维几何图形:会面问题、蒲丰(Buffon)投针问题
- 几何概率的基本性质
1.2.4 概率的性质
pass
1.3 常用概型公式
1.3.1 条件概率计算公式
1.3.2 乘法原理计算公式
基本 : 前提 : P ( A ) > 0 \text{基本}:\text{前提}:P(A)>0 P ( A B ) = P ( A ) P ( B ∣ A ) P(AB) = P(A)P(B|A) 推广 : 前提 : P ( A 1 A 2 , . . . , A n ) > 0 \text{推广}:\text{前提}:P(A_1A_2,...,A_n)>0 P ( A 1 A 2 . . . A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) ⋯ P ( A n ∣ A 1 A 2 . . . A n − 1 ) P(A_1A_2...A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2) \cdots P(A_n|A_1A_2...A_{n-1})
1.3.3 全概公式
我们将样本空间
1.3.4 贝叶斯公式
在上述全概公式的背景之下,现在希望求解事件
可以发现全概公式是计算事件发生的所有子样本空间的概率贡献,而贝叶斯公式是计算事件发生的总概率中某些子样本空间的概率贡献,前者是正向思维,后者是逆向思维
1.4 事件的独立性及伯努利概型
1.4.1 独立性
定义
基本:若
A , B A,B P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) 推广:若
A 1 , A 2 , . . . , A n A_1,A_2,...,A_n ∀ 1 ≤ i 1 < i 2 < ⋯ < i k ≤ n ( k = 2 , 3 , ⋯ , n ) s . t . P ( A i 1 A i 2 ⋯ A i k ) = P ( A i 1 ) P ( A i 2 ) ⋯ P ( A i k ) \begin{aligned}\forall \quad 1 \le i_1<i_2<\cdots<i_k \le n\ (k=2,3,\cdots,n) \\s.t. \quad P(A_{i_1}A_{i_2}\cdots A_{i_k}) = P(A_{i_1})P(A_{i_2})\cdots P(A_{i_k})\end{aligned}
定理
基本:若
A , B A,B A , B ‾ A,\overline{B} A ‾ , B \overline{A},B A ‾ , B ‾ \overline{A},\overline{B} 推广:若
A 1 , A 2 , . . . , A n A_1,A_2,...,A_n k ( 2 ≤ k ≤ n ) k(2 \le k \le n) P ( A i 1 ^ A i 2 ^ ⋯ A i k ^ ) = P ( A i 1 ^ ) P ( A i 2 ^ ) ⋯ P ( A i k ^ ) s . t . A i j ^ = A o r A ‾ ( j = 1 , 2 , ⋯ , k ) \begin{aligned}P(\hat{A_{i_1}}\hat{A_{i_2}}\cdots \hat{A_{i_k}}) = P(\hat{A_{i_1}})P(\hat{A_{i_2}})\cdots P(\hat{A_{i_k}}) \\s.t. \quad \hat{A_{i_j}} = A \ or \ \overline{A}\ (j=1,2,\cdots,k)\end{aligned}
概念辨析
两两独立:对于
n n 相互独立:对于
n n 2 → n 2 \to n 总结:对于
n n C n 2 C_n^2 2 n − ( n + 1 ) 2^n-(n+1) 两两独立 ⊂ 相互独立 \text{两两独立} \subset \text{相互独立}
1.4.2 伯努利概型
定义:
n n n n - 伯努利概型:每次试验只有两种可能的结果
模型:
二项概率公式:n 次独立重复试验发生 k 次的概率:
C n k p k ( 1 − p ) n − k C_n^k p^k (1-p)^{n-k} 几何概率公式:在第 n 次试验首次成功的概率:
( 1 − p ) n − 1 p (1-p)^{n-1}p
第2章 随机事件及其分布
我们知道,解决事件发生概率的问题,除了事件表示以外,我们还关心每一个事件发生的概率
- 首先介绍随机变量的概念以及分布函数的概念
- 接着介绍随机变量对应的概率发生情况组成的集合。离散型的叫分布列,连续型的叫概率密度函数,并在其中贯穿分布函数的应用
- 最后介绍分布函数的复合。从离散型和连续型随机变量两个方向展开
2.1 随机变量及其概率分布
2.1.1 随机变量的概念
总的来说,随机变量就是一个样本空间与实数集的映射。我们定义样本空间
2.1.2 随机变量的分布函数
- 分布函数的定义:
F ( x ) = P ( X ≤ x ) F(x)=P(X \le x) - 分布函数的性质:
- 非负有界性:
0 ≤ F ( x ) ≤ 1 0 \le F(x) \le 1 - 单调不减性:若
x 1 < x 2 x_1 < x_2 F ( x 1 ) ≤ F ( x 2 ) F(x_1) \le F(x_2) F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 \displaystyle F(-\infty) = \lim_{x \to -\infty} F(x) = 0 F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 \displaystyle F(+\infty) = \lim_{x \to +\infty} F(x) = 1 - 右连续性:
lim x → x 0 + F ( x ) = F ( x 0 ) ( − ∞ < x 0 < + ∞ ) \displaystyle \lim_{x\to x_0^+}F(x) = F(x_0)\quad(-\infty < x_0 < +\infty)
- 非负有界性:
2.2 离散型随机变量及其分布列
2.2.1 离散性随机变量的分布列
随机变量的取值都是整数,有以下三种表示方法
公式法
p k = P ( X = x k ) , k = 1 , 2 , ⋯ , p_k = P(X=x_k),\quad k = 1,2,\cdots, 服从法
X ∼ ( x 1 x 2 x 3 ⋯ p 1 p 2 p 3 ⋯ ) X \sim \begin{pmatrix}x_1 & x_2 & x_3 & \cdots \\p_1 & p_2 & p_3 & \cdots\end{pmatrix} 表格法
X x 1 x 2 x 3 ⋯ P p 1 p 2 p 3 ⋯ \begin{array}{c|cccc}X & x_1 & x_2 & x_3 & \cdots \\\hlineP & p_1 & p_2 & p_3 & \cdots\end{array}
2.2.2 常用离散性随机变量及其分布列
0-1分布:即一个事件只有两面性,我们称这样的随机变量服从0-1分布或者两点分布,记作
X ∼ ( 0 1 1 − p p ) X \sim \begin{pmatrix}0 & 1 \\1-p & p\end{pmatrix} 二项分布:其实就是 n 重伯努利试验,我们称这样的随机变量服从二项分布,分布列为
P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k) = C_n^kp^k(1-p)^{n-k} X ∼ B ( n , p ) X \sim B(n,p) 几何分布:同样是伯努利事件,现在需要求解第
k k P ( X = k ) = ( 1 − p ) k − 1 p P(X=k)=(1-p)^{k-1}p X ∼ G ( p ) X \sim G(p) 超几何分布:就是在 N 件含有 M 件次品的样品中无放回的抽取 n 件,问其中含有次品数量的分布列,为
P ( X = k ) = C M k C N − M n − k C N n , k = 0 , 1 , 2 , ⋯ , min ( n , M ) \displaystyle P(X=k)=\frac{C_M^k C_{N-M}^{n-k}}{C_N^n}, \quad k=0,1,2,\cdots,\min{(n, M)} X ∼ 超几何分布 ( n , N , M ) X \sim \text{超几何分布}(n,N,M) 泊松分布:当二项分布中,试验次数很大或者概率很小时,可以近似为泊松分布,即
P ( X = k ) = C n k p k ( 1 − p ) n − k → λ k k ! e − λ \displaystyle P(X=k)=C_n^k p^k(1-p)^{n-k} \to \frac{\lambda^k}{k!}e^{-\lambda} λ > 0 \lambda > 0 X ∼ P ( λ ) X \sim P(\lambda) 显然,泊松分布含有下面两个性质
P ( X = k ) > 0 , k = 0 , 1 , ⋯ P(X=k) > 0,k=0,1,\cdots ∑ k = 0 ∞ P ( X = k ) = 1 \displaystyle \sum_{k=0}^\infty P(X=k)=1 ▶泊松分布正规性证明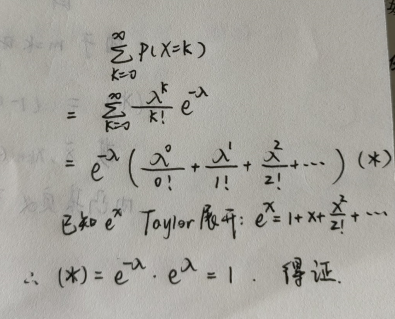
2.3 连续型随机变量及其概率密度函数
说白了其实就是离散性随机变量的积分加强版。现在随着事件发生的不同取值
2.3.1 连续型随机变量的密度函数
概率密度函数,简称:密度函数 or 概率密度
定义:设随机变量
X X F ( x ) F(x) p ( x ) p(x) X X p ( x ) p(x) X X ∀ x ∈ R , F ( x ) = ∫ − ∞ x p ( t ) d t \forall x \in R,F(x) = \int_{-\infty}^{x} p(t)dt 性质:
非负性:
p ( x ) ≥ 0 p(x) \ge 0 正规性:
∫ − ∞ + ∞ p ( x ) d x = 1 \int_{-\infty}^{+\infty} p(x)dx = 1 可积性:
∀ x 1 ≤ x 2 , P ( x 1 ≤ X ≤ x 2 ) = F ( x 2 ) − F ( x 1 ) = ∫ x 1 x 2 p ( x ) d x \forall x_1 \le x_2,P(x_1 \le X \le x_2) = F(x_2) - F(x_1) = \int_{x_1}^{x_2}p(x)dx 分布函数可导性:若
p ( x ) p(x) x x F ′ ( x ) = p ( x ) F'(x) = p(x) 已知事件但无意义性:
∀ x ∈ R , P ( X = x ) = F ( x ) − F ( x ) = 0 \forall x \in R, P(X=x) = F(x) - F(x) = 0 - 离散型变量可以通过列举随机变量
X X P ( A ) = 0 P(A) = 0 A A P ( A ) = 1 P(A)=1 A A - 对于连续型随机变量
X X P ( x 1 < X < X 2 ) = P ( x 1 < X ≤ X 2 ) = P ( x 1 ≤ X < X 2 ) = P ( x 1 ≤ X ≤ X 2 ) P(x_1 < X < X_2)=P(x_1 < X \le X_2)=P(x_1 \le X < X_2)=P(x_1 \le X \le X_2)
- 离散型变量可以通过列举随机变量
实际描述性:密度函数的数值反映了随机变量
X X x x p ( x ) Δ x ≈ ∫ x x + Δ x p ( t ) d t = F ( x + Δ x ) − F ( x ) = P ( x ≤ X ≤ x + Δ x ) p(x)\Delta x \approx \int_{x}^{x+\Delta x} p(t)dt = F(x+\Delta x) - F(x) = P(x \le X \le x+\Delta x)
2.3.2 常用连续型随机变量及其密度函数
| 分布定义式 | 概率密度函数 | 分布函数 | |
|---|---|---|---|
| 均匀分布 | |||
| 指数分布 | |||
| 正态分布 |
补充说明:
指数分布:其中参数
λ > 0 \lambda >0 正态分布:一般正态函数
F ( x ) F(x) Φ ( x ) \Phi(x) F ( x ) = Φ ( x − μ σ ) F(x) = \Phi(\frac{x - \mu}{\sigma}) 于是对于计算一般正态函数的函数值,就可以通过下式将其转化为标准正态函数,最后查表即可:
2.4 随机变量函数的分布
本目主要介绍给定一个随机变量
2.4.1 离散型随机变量函数的分布
通过关系式
2.4.2 连续型随机变量函数的分布
给定随机变量
方法一:先求解随机变量
Y Y F Y ( y ) F_Y(y) p Y ( y ) p_Y(y) 即先
F Y ( y ) = P Y ( Y ≤ y ) = P Y ( g ( X ) ≤ y ) = P X ( X ≤ f ( y ) ) = F X ( f ( y ) ) F_Y(y) = P_Y(Y \le y) = P_Y(g(X) \le y) = P_X(X \le f(y)) = F_X(f(y)) Y Y 再对
F Y ( y ) F_Y(y) p Y ( y ) = d d y F Y ( y ) = d d y F X ( f ( y ) ) = F X ′ ( f ( y ) ) ⋅ f ′ ( y ) = p X ( f ( y ) ) ⋅ f ′ ( y ) \displaystyle p_Y(y) = \frac{d}{dy} F_Y(y) = \frac{d}{dy} F_X(f(y)) = F_X'(f(y)) \cdot f'(y) = p_X(f(y)) \cdot f'(y) 方法二:如果关系式
y = g ( x ) y=g(x) x = h ( y ) x=h(y) Y Y p Y ( y ) p_Y(y) α \alpha β \beta Y = g ( X ) Y=g(X) x x h ( y ) h(y) y y p Y ( y ) = { p X ( h ( y ) ) ⋅ ∣ h ′ ( y ) ∣ , α < y < β 0 , 其他 p_Y(y) = \begin{cases}p_X(h(y)) \cdot |h'(y)|, & \alpha < y < \beta \\0, & \text{其他}\end{cases}
第3章 随机向量及其分布
实际生活中,只采用一个随机变量描述事件往往是不够的。本章引入多维的随机变量概念,构成随机向量,从二维开始,推广到
3.1 二维随机向量的联合分布
现在我们讨论二维随机向量的联合分布。所谓的联合分布,其实就是一个曲面的概率密度(离散型就是点集),而分布函数就是对其积分得到的三维几何体的体积(散点和)而已。
3.1.1 联合分布函数
定义:我们定义满足下式的二元函数

性质:其实配合几何意义理解就会很容易了
- 固定某一维度,另一维度是单调不减的
- 对于每个维度都是右连续的
- 固定某一维度,另一维度趋近于负无穷对应的函数值为
0 0 - 二维前缀和性质,右上角的矩阵面积
≥ 0 \ge 0
3.1.2 联合分布列
定义:若二维随机向量
表示:有两种表示二维随机向量分布列的方法,如下
公式法
p i j = P ( X = x i , Y = y i ) , i , j = 1 , 2 , ⋯ p_{ij} = P(X=x_i,Y = y_i), \quad i,j=1,2,\cdots 表格法:

性质:
- 非负性:
p i j ≥ 0 , i , j = 1 , 2 , ⋯ p_{ij} \ge 0, \quad i,j=1,2,\cdots - 正规性:
∑ i ∑ j p i j = 1 \displaystyle \sum_{i} \sum_{j} p_{ij} = 1
3.1.3 联合密度函数
定义:
性质:
- 非负性:
∀ x , y ∈ R , p ( x , y ) ≥ 0 \forall x,y \in R,p(x,y) \ge 0 - 正规性:
∫ − ∞ + ∞ ∫ − ∞ + ∞ p ( x , y ) d x d y = 1 \displaystyle \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} p(x,y)dxdy = 1
结论:
- 联合分布函数相比于一元分布函数,其实就是从概率密度函数与
x x x O y xOy - 若概率密度曲面在
x O y xOy
常见的连续型二维分布:
二维均匀分布:假设该曲面与
x O y xOy S S 1 S \frac{1}{S} p ( x , y ) = { 1 S , ( x , y ) ∈ G 0 , 其他 p(x,y) = \begin{cases}\frac{1}{S}, &(x,y) \in G \\0, &\text{其他}\end{cases} 二元正态分布:不要求掌握密度函数,可以感受一下密度函数的图像:
▶二元正态分布 - 密度函数的图像
计算题:往往给出一个二元密度函数,然后让我们求解(1)密度函数中的参数、(2)分布函数、(3)联合事件某个区域下的概率
(1)我们利用二元密度函数的正规性,直接积分值为
(2)划分区间后进行曲面积分即可,在曲面积分时往往结合
(3)画出概率密度曲面在
3.2 二维随机向量的边缘分布
对于二元分布函数,我们也可以研究其中任意一个随机变量的分布情况,而不需要考虑另一个随机变量的取值情况。举一个实例就是,假如当前的随机向量是身高和体重,所谓的只研究其中一个随机变量,即边缘分布函数的情形就是,我们不考虑身高只考虑体重的分布情况;或者我们不考虑体重,只考虑身高的分布情况。接下来,我们将从边缘分布函数入手,逐渐学习离散型的分布列与连续型的分布函数。
3.2.1 边缘分布函数
我们称
3.2.2 边缘分布列
所谓的边缘分布列,就是固定一个随机变量,另外的随机变量取遍,组成的分布列。即:
我们称:
P ( X = x i ) P(X=x_i) ( X , Y ) (X,Y) X X P ( Y = y j ) P(Y=y_j) ( X , Y ) (X,Y) Y Y
3.2.3 边缘密度函数
所谓的的边缘密度函数,可以与边缘分布列进行类比,也就是固定一个随机变量,另外的随机变量取遍。只不过连续型的取遍就是无数个点,而离散型的取遍是可列个点,仅此而已。即:
我们称:
P ( X = x ) P(X=x) ( X , Y ) (X,Y) X X P ( Y = y ) P(Y=y) ( X , Y ) (X,Y) Y Y
3.3 随机向量的条件分布
本目主要介绍的是条件分布。所谓的条件分布,其实就是在约束一个随机变量为定值的情况下,另外一个随机变量的取值情况。与上述联合分布、边缘分布的区别在于:
- 联合分布、边缘分布的分布函数是一个体积(散点和),概率密度(分布列)是一个曲面(点集)
- 条件分布的分布函数是一个面积(散点和),概率密度(分布列)是一个曲线(点集)
3.3.1 离散型随机向量的条件分布列和条件分布函数
条件分布列,即散点情况:
我们称:
p i ∣ j p_{i|j} Y = y j Y=y_j X X p j ∣ i p_{j|i} X = x i X=x_i Y Y
条件分布函数,即点集情况:
我们称:
F ( x ∣ y j ) F(x|y_j) Y = y j Y=y_j X X F ( y ∣ x i ) F(y|x_i) X = x i X=x_i Y Y
3.3.2 连续型随机向量的条件密度函数和条件分布函数
条件密度函数,即联合分布的概率密度曲面上,约束了某一维度的随机变量为定值,于是条件密度函数的图像就是一个空间曲线:
我们称:
p ( x ∣ y ) p(x|y) Y = y Y=y X X p ( y ∣ x ) p(y|x) X = x X=x Y Y
条件分布函数,即上述曲线的分段积分结果:
我们称:
F ( x ∣ y ) F(x|y) Y = y Y=y X X F ( y ∣ x ) F(y|x) X = x X=x Y Y
3.4 随机变量的独立性
本目主要介绍随机变量的独立性。我们知道随机事件之间是有独立性的,即满足
定义:我们定义如果两个随机变量的分布函数满足下式,则两个随机变量相互独立:
F ( x , y ) = F X ( x ) F Y ( y ) F(x,y)=F_X(x)F_Y(y) 性质:对于随机向量
( X , Y ) (X,Y) 随机变量
X X Y Y 离散型: P ( X = x i , Y = y j ) = P ( X = x i ) P ( Y = y j ) 连续型: p ( x , y ) = p X ( x ) p Y ( y ) \begin{aligned}\text{离散型:}& P(X=x_i,Y=y_j) = P(X=x_i)P(Y=y_j) \\\text{连续型:}& p(x,y) = p_X(x)p_Y(y)\end{aligned} 若随机变量
X X Y Y h ( ⋅ ) h(\cdot) g ( ⋅ ) g(\cdot) h ( X ) , g ( Y ) h(X),g(Y)
3.5 随机向量函数的分布
在 2.4 目中我们了解到了随机变量函数的分布,现在我们讨论随机向量函数的分布。在生活中,假设我们已经知道了一个人群中所有人的身高和体重的分布情况,现在想要血糖根据身高和体重的分布情况,就需要用到本目的理念。我们从离散型和连续型随机向量
3.5.1 离散型随机向量函数的分布
按照规则枚举即可。
3.5.2 连续型随机向量函数的分布
与连续型随机变量函数的分布类似,这类题目一般也是:给定随机向量
(1) 和的分布:
先求分布函数
F Z ( z ) F_Z(z) F Z ( z ) = P ( X + Y ≤ z ) = ∬ x + y ≤ z p ( x , y ) d x d y = ∫ − ∞ z [ ∫ − ∞ + ∞ p ( x , t − x ) d x ] d t = ∫ − ∞ z [ ∫ − ∞ + ∞ p ( t − y , y ) d y ] d t \begin{aligned}F_Z(z) &= P(X+Y \le z) \\&= \iint\limits_{x+y \le z} p(x,y) dxdy \\&\begin{align}&= \int _{-\infty}^z \left [ \int_{-\infty}^{+\infty} p(x,t-x)dx \right ] dt \\&= \int _{-\infty}^z \left [ \int_{-\infty}^{+\infty} p(t-y,y)dy \right ] dt\end{align}\end{aligned} 由分布函数定义:
F X ( x ) = ∫ − ∞ x p ( u ) d u F_X(x) = \int_{-\infty}^xp(u)du 所以可得
Z = X + Y Z=X+Y p Z ( z ) p_Z(z) p Z ( z ) = ∫ − ∞ + ∞ p ( x , z − x ) d x ( 1 ) p Z ( z ) = ∫ − ∞ + ∞ p ( z − y , y ) d y ( 2 ) \begin{aligned}p_Z(z) = \int_{-\infty}^{+\infty} p(x,z-x)dx \quad &(1) \\p_Z(z) = \int_{-\infty}^{+\infty} p(z-y,y)dy \quad &(2) \\\end{aligned} 若 X 和 Y 相互独立,还可得卷积式:
p Z ( z ) = ∫ − ∞ + ∞ p ( x , z − x ) d x = ∫ − ∞ + ∞ p X ( x ) ⋅ p Y ( z − x ) d x ( 1 ) p Z ( z ) = ∫ − ∞ + ∞ p ( z − y , y ) d y = ∫ − ∞ + ∞ p X ( z − y ) ⋅ p Y ( y ) d y ( 2 ) \begin{aligned}p_Z(z) &= \int_{-\infty}^{+\infty} p(x,z-x)dx \\&= \int_{-\infty}^{+\infty} p_X(x)\cdot p_Y(z-x) dx \quad &(1) \\p_Z(z) &= \int_{-\infty}^{+\infty} p(z-y,y)dy \\&= \int_{-\infty}^{+\infty} p_X(z-y)\cdot p_Y(y) dy \quad &(2)\end{aligned}
(2) 次序统计量的分布(对于两个相互独立的随机变量 X 和 Y):
对于
M = max ( X , Y ) M=\max{(X,Y)} F M ( z ) = P ( M ≤ z ) = P ( max ( X , Y ) ≤ z ) = P ( X ≤ z , Y ≤ z ) = P ( X ≤ z ) ⋅ P ( Y ≤ z ) = F X ( z ) ⋅ F Y ( z ) \begin{aligned}F_M(z) &= P(M \le z) \\&= P(\max{(X,Y)} \le z) \\&= P(X \le z, Y \le z) \\&= P(X \le z) \cdot P(Y \le z) \\&= F_X(z) \cdot F_Y(z)\end{aligned} 对于
N = min ( X , Y ) N=\min{(X,Y)} F N ( z ) = P ( N ≤ z ) = P ( min ( X , Y ) ≤ z ) = 1 − P ( min ( X + Y ) ≥ z ) = 1 − P ( X ≥ z , Y ≥ z ) = 1 − P ( X ≥ z ) ⋅ P ( Y ≥ z ) = 1 − [ 1 − F X ( z ) ] ⋅ [ 1 − F Y ( z ) ] \begin{aligned}F_N(z) &= P(N \le z) \\&= P(\min{(X,Y)} \le z) \\&= 1 - P(\min{(X+Y)} \ge z) \\&= 1 - P(X \ge z,Y \ge z) \\&= 1 - P(X \ge z) \cdot P(Y \ge z) \\&= 1 - [1 - F_X(z)] \cdot [1 - F_Y(z)]\end{aligned} 若拓展到
n n F M ( z ) = [ F ( z ) ] n p M ( z ) = n p ( z ) [ F ( z ) ] n − 1 \begin{aligned}F_M(z) &= [F(z)]^n \\p_M(z) &= np(z)[F(z)]^{n-1}\end{aligned} F N ( z ) = 1 − [ 1 − F ( z ) ] n p N ( z ) = n p ( z ) [ 1 − F ( z ) ] n − 1 \begin{aligned}F_N(z) &= 1 - [1-F(z)]^n \\p_N(z) &= np(z)[1-F(z)]^{n-1}\end{aligned}
第4章 随机变量的数字特征
本章我们将学习随机变量的一些数字特征。所谓的数字特征其实就是随机变量分布的一些内在属性,比如均值、方差、协方差等等,有些分布特性甚至可以通过某个数字特征而直接觉得。其中期望和方差往往用来衡量单个随机变量的特征,而协方差与相关系数则是用来衡量随机变量之间的数字特征。接下来开始介绍。
4.1 数学期望
加权平均概念的严格数学定义。
4.1.1 随机变量的数学期望
离散型
E X = ∑ i = 1 ∞ x i p i EX = \sum_{i=1}^{\infty} x_i p_i 连续型
E X = ∫ − ∞ + ∞ x p ( x ) d x \begin{aligned}&EX = \int_{-\infty}^{+\infty} xp(x)dx\end{aligned}
4.1.2 随机变量函数的数学期望
离散型
一元
E g ( X ) = ∑ i = 1 ∞ g ( x i ) p i Eg(X) = \sum_{i=1}^{\infty}g(x_i)p_i 二元
E g ( X , Y ) = ∑ i = 1 ∞ ∑ j = 1 ∞ g ( x i , y i ) p i j Eg(X,Y) = \sum_{i=1}^{\infty}\sum_{j=1}^{\infty}g(x_i,y_i)p_{ij}
连续型
一元
E g ( X ) = ∫ − ∞ + ∞ g ( x ) p ( x ) d x Eg(X) = \int_{-\infty}^{+\infty}g(x)p(x)dx 二元
E g ( X , Y ) = ∫ − ∞ + ∞ ∫ − ∞ + ∞ g ( x i , y i ) p ( x , y ) d x d y Eg(X,Y) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x_i,y_i)p(x,y)dxdy
4.1.3 数学期望的性质
E C = C EC=C E ( C X ) = C E X E(CX)=CEX E ( X + Y ) = E X + E Y E(X+Y)=EX+EY - 若
X X Y Y E ( X Y ) = E X E Y E(XY)=EXEY
4.2 方差
随机变量的取值与均值之间的离散程度。
4.2.1 方差的定义
我们定义随机变量
4.2.2 方差的性质
下列方差的性质全部可由上述方差的定义式,结合期望的性质推导而来:
D ( a X + b ) = a 2 D ( X ) D(aX+b) = a^2D(X) 若
X 1 , X 2 , ⋯ X_1,X_2,\cdots D ( a X 1 ± b X 2 ± ⋯ ) = a 2 D ( X 1 ) + b 2 D ( X 2 ) + ⋯ D(aX_1 \pm bX_2 \pm \cdots) = a^2D(X_1) + b^2D(X_2) + \cdots E [ ( X − E X ) 2 ] ≤ E [ ( X − C ) 2 ] E\left[ (X-EX)^2 \right] \le E \left [ (X-C)^2 \right ] 切比雪夫不等式
(本以为不要求掌握的,但是被小测拷打了,补一下):∀ ϵ > 0 , P ( ∣ X − E X ∣ < ϵ ) ≥ 1 − D X ϵ 2 \forall \epsilon >0, P(|X - EX| < \epsilon) \ge 1 - \frac{DX}{\epsilon^2}
4.3 结论与推导(补)
| 类型 | 分布 | 符号 | 期望 | 方差 |
|---|---|---|---|---|
| 离散型 | 0-1 分布 | |||
| — | *二项分布 | |||
| — | 几何分布 | |||
| — | *泊松分布 | |||
| 连续型 | 均匀分布 | |||
| — | 指数分布 | |||
| — | *正态分布 |
注:打星号表示在两个随机变量
X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) → X ± Y ∼ N ( μ 1 ± μ 2 , σ 1 2 + σ 2 2 ) X \sim N(\mu_1,\sigma_1^2), Y \sim N(\mu_2,\sigma_2^2) \to X\pm Y\sim N(\mu_1\pm\mu_2,\sigma_1^2+\sigma_2^2) X ∼ B ( n 1 , p ) , Y ∼ B ( n 2 , p ) → X + Y ∼ B ( n 1 + n 2 , p ) X \sim B(n_1,p), Y \sim B(n_2,p) \to X+Y\sim B(n_1+n_2,p) X ∼ P ( λ 1 ) , Y ∼ P ( λ 2 ) → X + Y ∼ P ( λ 1 + λ 2 ) X \sim P(\lambda_1),Y\sim P(\lambda_2) \to X+Y \sim P(\lambda_1+\lambda_2)
推导的根本方式还是从定义出发。当然为了省事也可以从性质出发。
0-1 分布
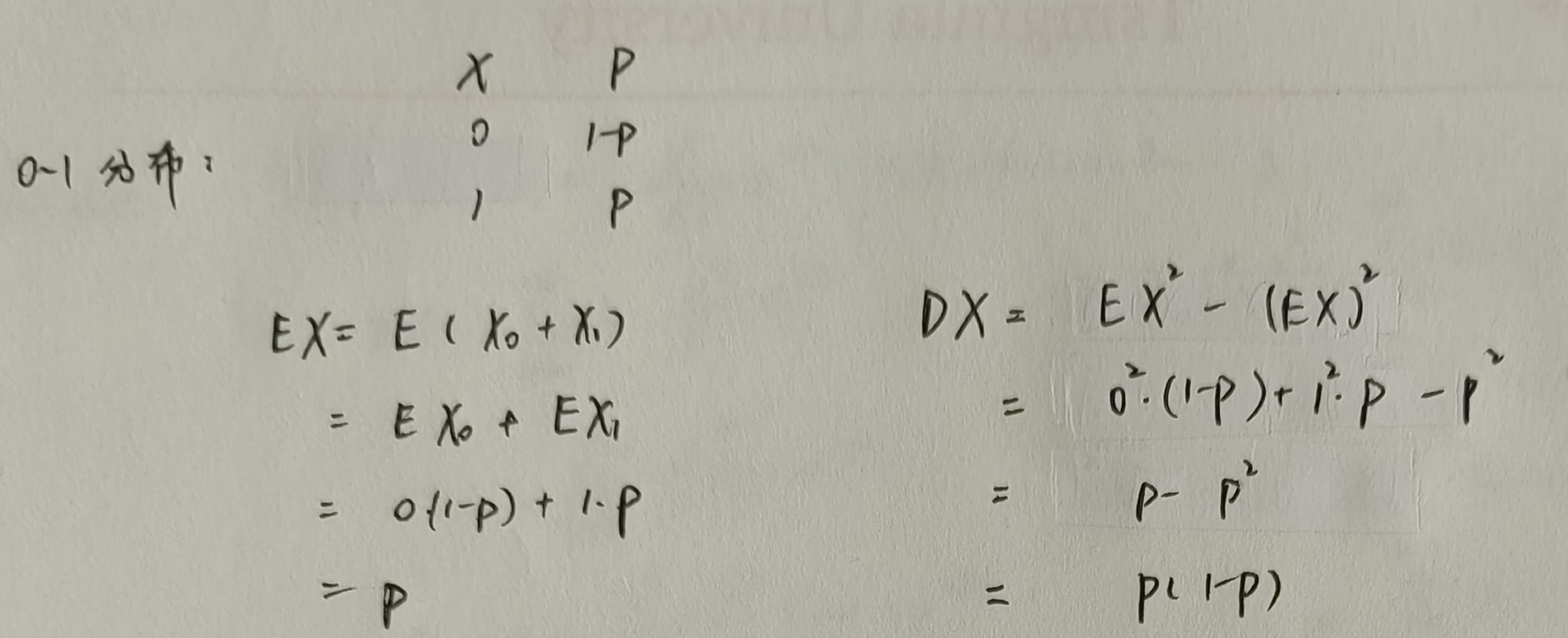
二项分布
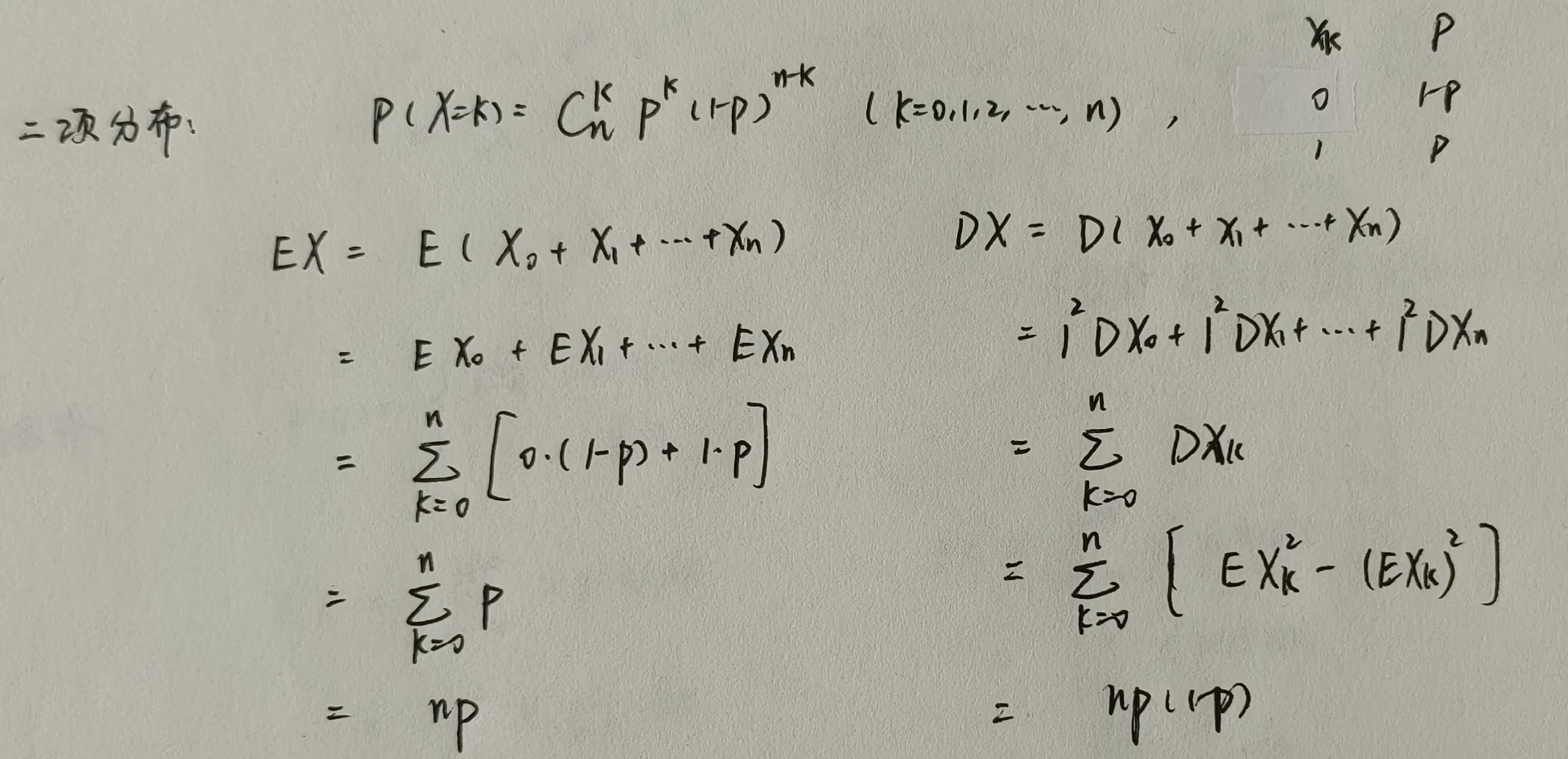
几何分布
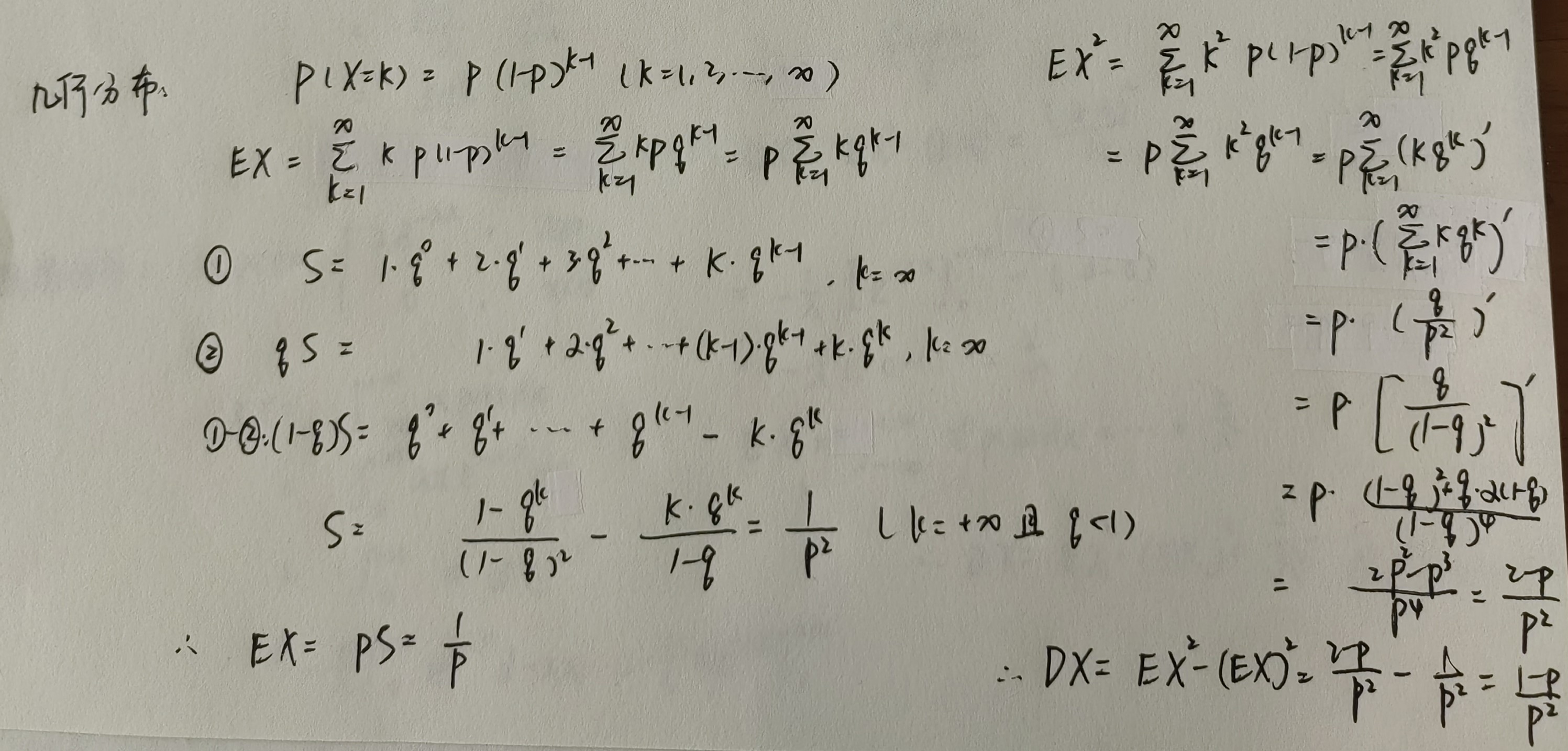
泊松分布
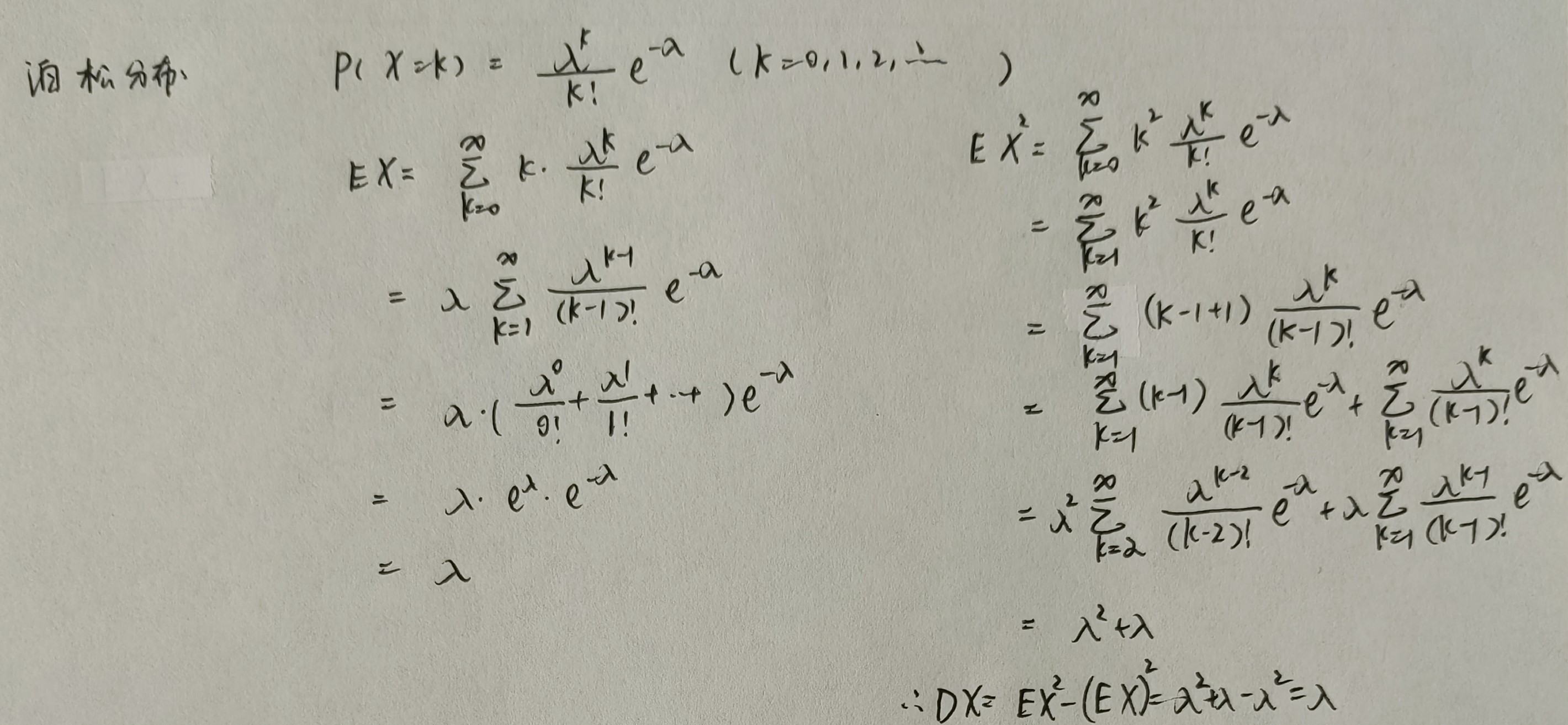
均匀分布
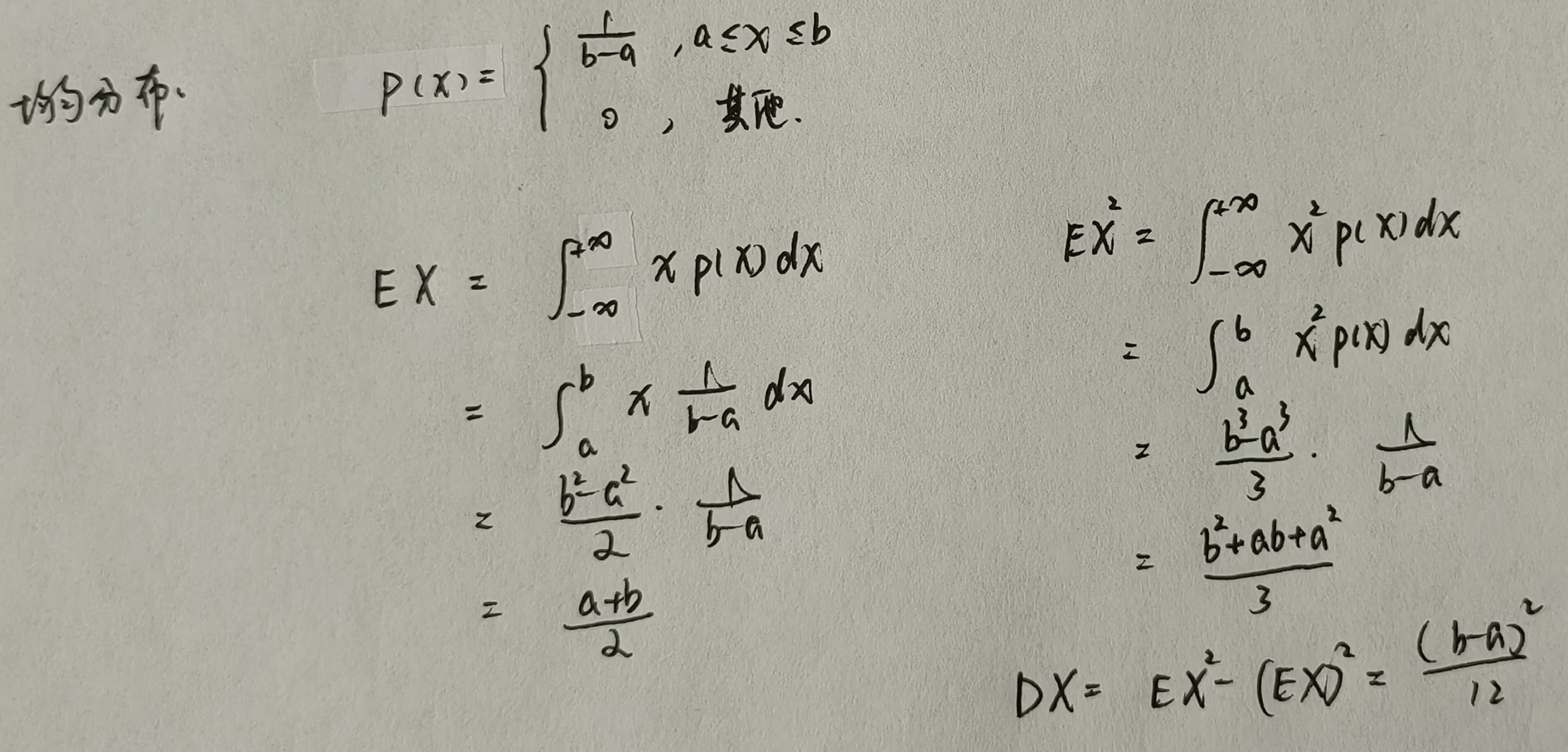
指数分布
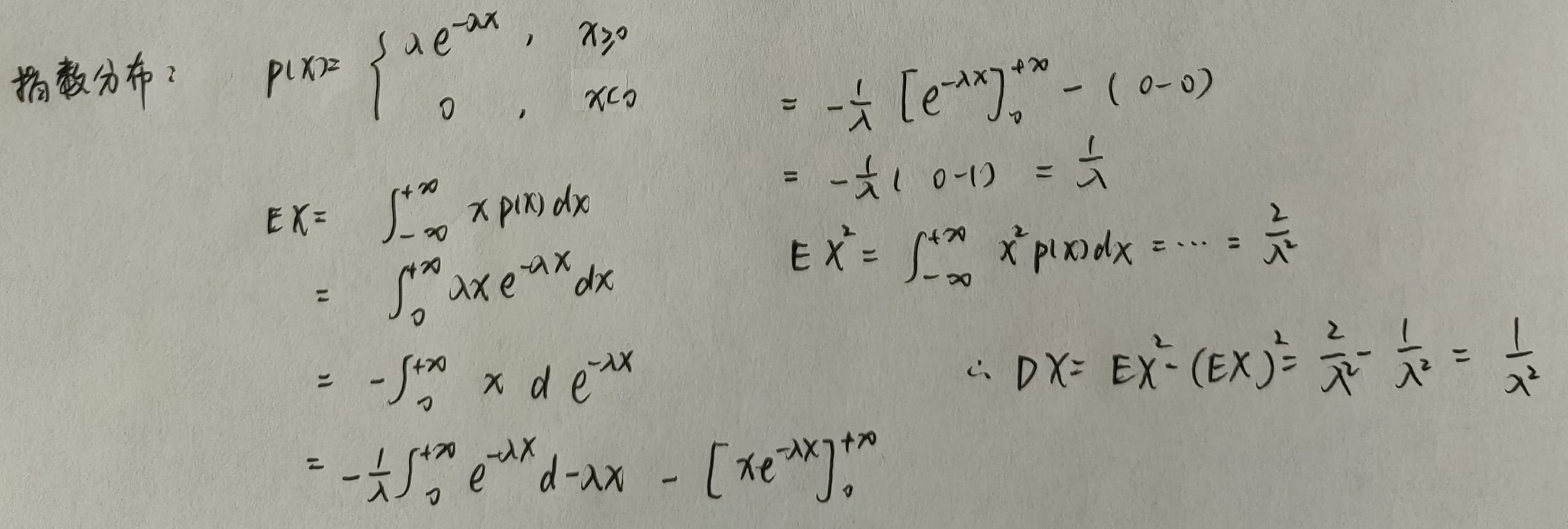
4.4 协方差与相关系数
4.4.1 协方差
定义:随机变量 X 与 Y 的协方差
特别的:
性质:
- 交换律:
C o v ( X , Y ) = C o v ( Y , X ) Cov(X,Y)=Cov(Y,X) - 提取率:
C o v ( a X , b Y ) = a b C o v ( X , Y ) Cov(aX,bY)=abCov(X,Y) - 分配率:
C o v ( X 1 + X 2 , Y ) = C o v ( X 1 , Y ) + C o v ( X 2 , Y ) Cov(X_1+X_2,Y) = Cov(X_1,Y)+Cov(X_2,Y) - 独立性:若 X 与 Y 相互独立,则
C o v ( X , Y ) = 0 Cov(X,Y)=0 - 放缩性:
[ C o v ( X , Y ) ] 2 ≤ D X ⋅ D Y \left[Cov(X,Y)\right]^2 \le DX \cdot DY
4.4.2 相关系数
定义:相关系数
特别的:
- 若
0 < ρ < 1 0 < \rho < 1 - 若
− 1 < ρ < 0 -1<\rho<0
性质:
- 放缩性(由协方差性质5可得):
∣ ρ ∣ ≤ 1 |\rho| \le 1 - 独立性(由协方差性质4可得):若 X 与 Y 相互独立,则
p = 0 p=0 - 线性相关性(不予证明):
∣ ρ ∣ = 1 |\rho|=1 a ( a ≠ 0 ) , b a(a\ne0),b P ( Y = a X + b ) = 1 P(Y=aX+b)=1
4.4.3 独立性与线性相关性(补)
一般的:对于两个随机变量
X X Y Y → \rightarrow X X Y Y X X Y Y ↚ \nleftarrow X X Y Y X X Y Y
特别的:对于满足二维正态分布的随机变量
X X Y Y → \rightarrow X X Y Y X X Y Y ← \leftarrow X X Y Y
第5章 大数定律与中心极限定理
本章只需要知道一个独立同分布中心极限定理即可,至于棣莫弗-拉普拉斯中心极限定理其实就是前者的
独立同分布中心极限定理
定义:
解释:其实就是对于独立同分布的随机事件
第6章 数理统计的基本概念
开始统计学之旅。
6.1 总体与样本
类比 ML:数据集=总体,样本=样本。
我们只研究一种样本:简单随机样本
( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n)
同样的,我们研究总体
分布:由于样本相互独立,故:
F ( x 1 , x 2 , . . . , x n ) = F ( x 1 ) F ( x 2 ) ⋯ F ( x n ) F(x_1,x_2,...,x_n)=F(x_1)F(x_2) \cdots F(x_n) 联合密度:同样由于样本相互独立,故:
p ( x 1 , x 2 , . . . , x n ) = p ( x 1 ) p ( x 2 ) ⋯ p ( x n ) p(x_1,x_2,...,x_n)=p(x_1)p(x_2) \cdots p(x_n)
6.2 经验分布与频率直方图
经验分布函数是利用样本得到的。也是给区间然后统计样本频度进而计算频率,只不过区间长度不是固定的。
频率直方图就是选定固定的区间长度,然后统计频度进而计算频率作图。
6.3 统计量
统计量定义:关于样本不含未知数的表达式。
常见统计量:假设
一、样本均值和样本方差
样本均值:
X ‾ = 1 n ∑ i = 1 n X i \displaystyle \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i 样本方差:
S 0 2 = 1 n ∑ i = 1 n ( X i − X ‾ ) 2 = 1 n ∑ i = 1 n X i 2 − X ‾ 2 \displaystyle S_0^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \overline{X})^2 = \frac{1}{n}\sum_{i=1}^n X_i^2 - \overline{X}^2 样本标准差:
S 0 = S 0 2 \displaystyle S_0 = \sqrt{S_0^2} 修正样本方差:
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 \displaystyle S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X})^2 修正样本标准差:
S = S 2 \displaystyle S = \sqrt{S^2} ▶推导设总体
X X μ \mu σ 2 \sigma^2 ( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) 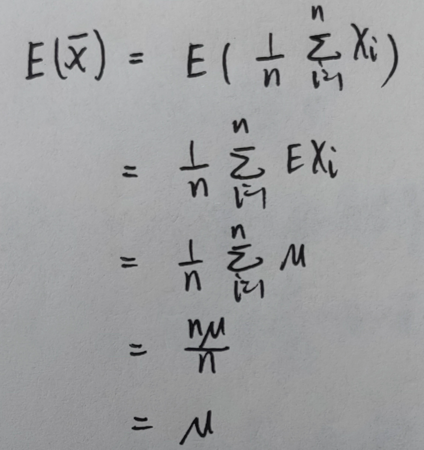
即:样本均值的数学期望
= = 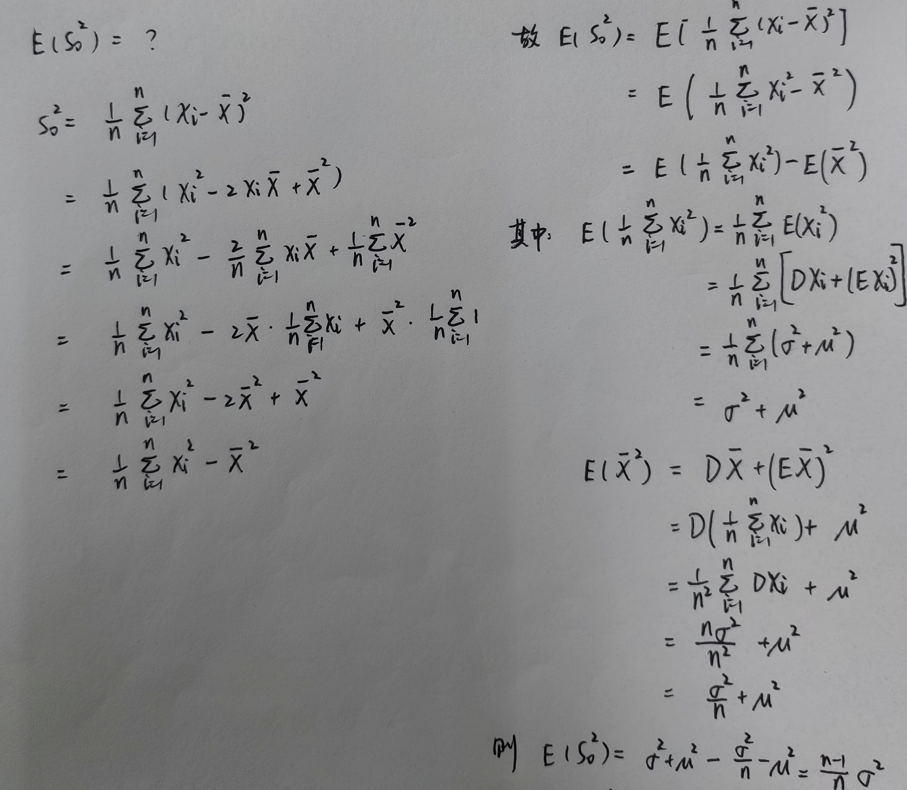
即:样本方差的数学期望
≠ \ne 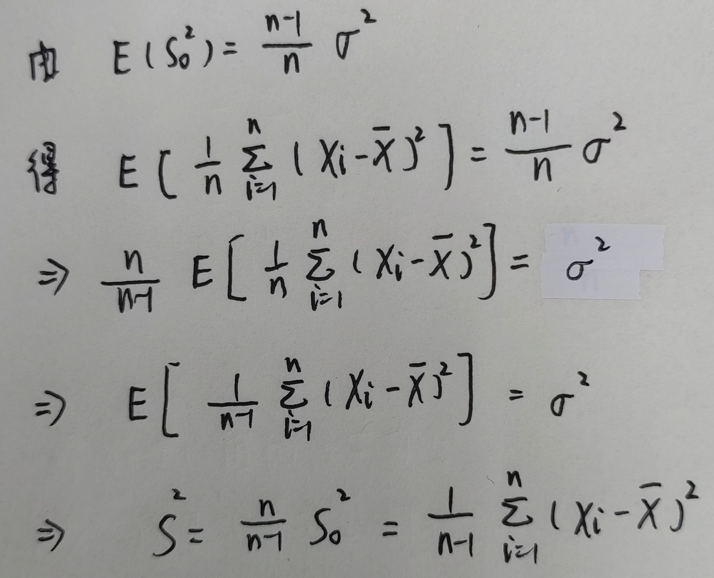
上图即:修正样本方差推导
样本
k k A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , ⋯ \displaystyle A_k = \frac{1}{n} \sum_{i=1}^n X_i^k,\quad k=1,2,\cdots 样本
k k B k = 1 n ∑ i = 1 n ( X i − X ‾ ) k , k = 2 , 3 , ⋯ \displaystyle B_k = \frac{1}{n} \sum_{i=1}^n (X_i-\overline{X})^k,\quad k=2,3,\cdots
二、次序统计量
- 序列最小值
- 序列最大值
- 极差 = 序列最大值 - 序列最小值
6.4 正态总体抽样分布定理
时刻牢记一句话:构造性定义!
6.4.1 卡方分布、t 分布、F 分布
分位数
- 我们定义实数
λ α \lambda_\alpha X X α \alpha P ( X > λ α ) = α P(X > \lambda_\alpha) = \alpha - 我们定义实数
λ 1 − β \lambda_{1-\beta} X X β \beta P ( X < λ 1 − β ) = β P(X < \lambda_{1-\beta})=\beta

定义:
- 对于
n n X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots ,X_n Y = X 1 2 + X 2 2 + ⋯ + X n 2 Y = X_1^2 + X_2^2 + \cdots + X_n^2 - 则
Y Y n n χ 2 \chi^2 Y ∼ χ 2 ( n ) Y \sim \chi^2(n)
性质:
可加性:若
Y 1 ∼ χ 2 ( n 1 ) , Y 2 ∼ χ 2 ( n 2 ) Y_1 \sim \chi^2(n_1), Y_2 \sim \chi^2(n_2) Y 1 , Y 2 Y_1,Y_2 Y 1 + Y 2 ∼ χ 2 ( n 1 + n 2 ) Y_1+Y_2 \sim \chi^2(n_1+n_2) 统计性:对于
Y ∼ χ 2 ( n ) Y \sim \chi^2(n) E Y = n , D Y = 2 n EY = n, DY = 2n ▶推导EY 的推导利用:
E X 2 = D X − ( E X ) 2 EX^2 = DX - (EX)^2 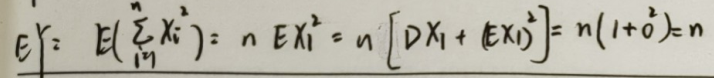
DY 的推导利用:方差计算公式、随机变量函数的数学期望进行计算


定义:
- 若随机变量
X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0, 1),Y \sim \chi^2 (n) X , Y X,Y - 则称随机变量
T = X Y / n T = \displaystyle \frac{X}{\sqrt{Y/n}} n n t t T ∼ t ( n ) T \sim t(n)
性质:
- 密度函数是偶函数,具备对称性

定义:
- 若随机变量
X ∼ χ 2 ( m ) , Y ∼ χ 2 ( n ) X \sim \chi^2(m), Y \sim \chi^2(n) - 则称随机变量
G = X / m Y / n G=\displaystyle \frac{X/m}{Y/n} ( m , n ) (m,n) F F G ∼ F ( m , n ) G \sim F(m, n)
性质:
- 倒数自由度转换:
1 G ∼ F ( n , m ) \displaystyle \frac{1}{G} \sim F(n, m) - 三变性质:
F 1 − α ( m , n ) = [ F α ( n , m ) ] − 1 \displaystyle F_{1-\alpha}(m, n) = \left [F_\alpha (n, m)\right]^{-1}
6.4.2 正态总体抽样分布基本定理
设
定理:
X ‾ ∼ N ( μ , σ 2 n ) \displaystyle \overline{X} \sim N(\mu, \frac{\sigma^2}{n}) ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \displaystyle \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) X ‾ \overline{X} S 2 S^2
推论:
n ( X ‾ − μ ) S ∼ t ( n − 1 ) \displaystyle \frac{\sqrt{n}(\overline{X} - \mu)}{S} \sim t(n-1)
第7章 参数估计
有些时候我们知道数据的分布类型,但是不清楚表达式中的某些参数,这就需要我们利用「已有的样本」对分布表达式中的参数进行估计。本章我们将从点估计、估计评价、区间估计三部分出发进行介绍。
7.1 点估计
所谓点估计策略,就是直接给出参数的一个估计值。本目我们介绍点估计策略中的两个方法:矩估计法、极大似然估计法。
7.1.1 矩估计法
其实就一句话:我们用样本的原点矩
7.1.2 极大似然估计法
基本原理是:在当前样本数据的局面下,我们希望找到合适的参数使得当前的样本分布情况发生的概率最大。由于各样本相互独立,因此我们可以用连乘的概率公式来计算当前局面的概率值:
上述
- 写出似然函数
L ( θ ) L(\theta) - 将上述似然函数取对数
- 求对数似然函数关于所有未知参数的偏导并计算极值点
- 解出参数关于样本统计量的表达式
离散型随机变量的似然函数表达式
连续型随机变量的似然函数表达式
可以看出极大似然估计本质上就是一个多元函数求极值的问题。特别地,当我们没法得到参数关于样本统计量的表达式
7.2 估计量的评价标准
如何衡量不同的点估计方法好坏?我们引入三种点估计量的评价指标:无偏性、有效性、一致性。其中一致性一笔带过,不做详细讨论。补充一点,参数的估计量
7.2.1 无偏性
顾名思义,就是希望估计出来的参数量尽可能不偏离真实值。我们定义满足下式的估计量
7.2.2 有效性
有效性是基于比较的定义方法。对于两个无偏估计
7.2.3 一致性
即当样本容量 n 趋近于无穷时,参数的估计值也能趋近于真实值,则称该估计量
7.3 区间估计
由于点估计只能进行比较,无法对单一估计进行性能度量。因此引入「主元法」的概念与「区间估计」策略
7.3.1 基本概念
可靠程度:参数估计区间越长,可靠程度越高
精确程度:参数估计区间越短,可靠程度越高
7.3.2 区间估计常用方法之主元法
主元法的核心逻辑就一个:在已知数据总体分布的情况下,构造一个关于样本
7.3.3 正态总体的区间估计
我们只需要掌握「一个总体服从正态分布」的情况。这种情况下的区间估计分为三种,其中估计均值
- 构造主元
Z ( X , θ ) Z(X,\theta) - 利用置信度
1 − α 1-\alpha Z Z - 对主元
Z Z θ \theta
为了提升区间估计的可信度,我们希望上述第 2 步计算出来的关于主元的取值范围尽可能准确。我们不加证明的给出以下结论:取主元的取值范围为 主元服从的分布的上下
(一) 求
构造主元
利用置信度
对主元
(二) 求
构造主元
利用置信度
对主元
(三) 求
构造主元
利用置信度
对主元
第8章 假设检验
第 7 章的参数估计是在总体分布已知且未知分布表达式中某些参数的情况下,基于「抽取的少量样本」进行的参数估计。
现在的局面同样,我们已知总体分布和不完整的分布表达式参数。现在需要我们利用抽取的少量样本判断样本所在向量空间是否符合某种性质。本章的「假设检验」策略就是为了解决上述情况而诞生的。我们主要讨论单个正态总体的情况并针对均值和方差两个参数进行假设和检验:
- 假设均值满足某种趋势,利用已知数据判断假设是否成立
- 假设方差满足某种趋势,利用已知数据判断假设是否成立
8.1 假设检验的基本概念
基本思想:首先做出假设并构造一个关于样本观察值和已知参数的检验统计量,接着计算假设发生的情况下小概率事件发生时该检验统计量的取值范围(拒绝域),最终代入已知样本数据判断计算结果是否在拒绝域内。如果在,则说明在当前假设的情况下小概率事件发生了,对应的假设为假;反之说明假设为真。
为了量化「小概率事件发生」这个指标,我们引入显著性水平
基于数据的实验导致我们无法避免错误,因此我们定义以下两类错误:
- 第一类错误:弃真错误。即假设正确,但由于数据采样不合理导致拒绝了真实的假设
- 第二类错误:存伪错误。即假设错误,同样因为数据的不合理导致接受了错误的假设
8.2 单个正态总体均值的假设检验
设
当总体方差
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
当总体方差
注:之所以这样构造是因为当总体
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
8.3 单个正态总体方差的假设检验
设
我们直接构造样本统计量
- 检验是否则求解双侧
α \alpha - 检验单边则求解单侧
α \alpha
前言
学科地位:
| 主讲教师 | 学分配额 | 学科类别 |
|---|---|---|
| 段博佳 | 3 | 自发课 |
成绩组成:
| 平时(5次作业+签到) | 期末(书本+讲义) |
|---|---|
| 60% | 40% |
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 算法设计与分析 | 《算法设计与分析(python版)》 | 1 | 王秋芬 | 清华大学出版社 | 978-7-302-57072-1 |
一、贪心
Dijkstra、Prim、Kruskal、Huffman
二、分治
二分、归并、快排(第 k 个数)
三、动规
- 区间dp:矩阵连乘
- 网格图dp:LCS
- 背包:完全背包、多重背包
四、深搜
- 排列树:TSP、图染色、调度、n 皇后
- 子集树:01背包
考后碎碎念
考的中规中矩,但是忘带修正带导致卷面一坨hh。按照试卷顺序罗列一下:表达式树、大根堆、Dijkstra、图染色、第 k 个数、Kruskal、完全背包。
试卷一看就是 wq 出的,但还是用 python 写的代码。有一说一这次考试还加深了我对快排的理解,尤其是在让我给出分治后的序列时hh。硬要按照上面四个标签分类的话大概就是:
- 贪心:Dijkstra、Kruskal
- 分治:第 k 个数
- 动规:完全背包
- 深搜:表达式树、大根堆、图染色
效果演示
[!note]
以下为课设报告内容
一、必做题
题目:编程实现希尔、快速、堆排序、归并排序算法。要求随机产生 10000 个数据存入磁盘文件,然后读入数据文件,分别采用不同的排序方法进行排序,并将结果存入文件中。
1.1 数据结构设计与算法思想
本程序涉及到四种排序算法,其中:
- 希尔排序:通过倍增方法逐渐扩大选择插入数据量的规模,而达到减小数据比较的次数,时间复杂度优化到近似
O ( n 1.65 ) O(n^{1.65}) - 快速排序:通过分治的算法策略,不断确定每一个数的最终位置,从而达到近似
O ( n log n ) O(n \log n) - 堆排序:通过堆的树形结构,减小两数的比较次数,最终通过不断维护堆结构来获得有序序列,时间复杂度为
O ( n log n ) O(n \log n) - 归并排序:通过分治排序回溯时左右两支有序的特点,进行归并,使算法整体的时间复杂度为固定的
O ( n log n ) O(n \log n)
1.2 程序结构
为了更好的了解排序算法内部的机制,我统计了每一种排序算法内部的比较次数,并结合了 Qt 的可视化框架进行编写。将四种排序作为算法内核嵌入 GUI 界面,程序结构如下:
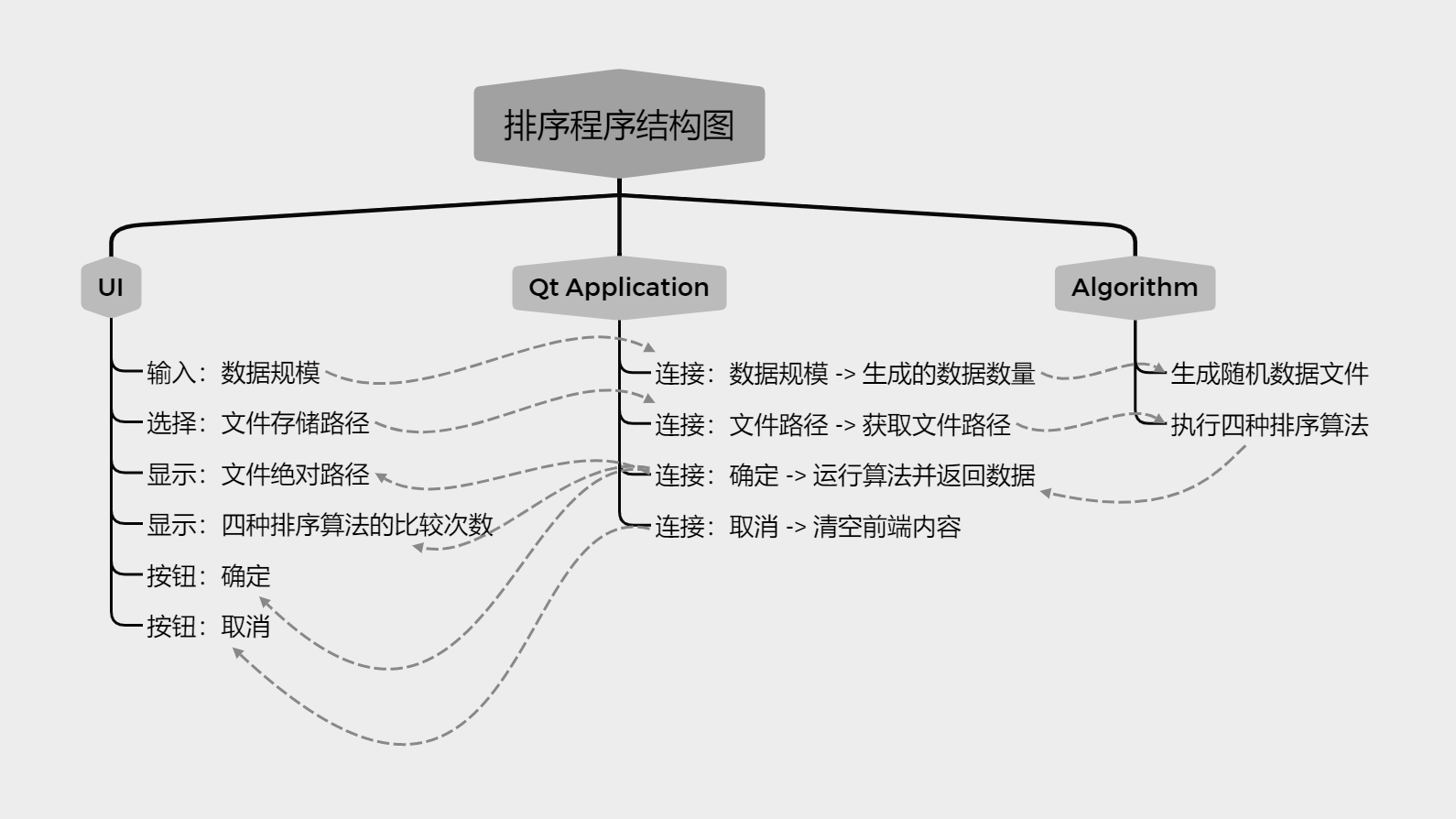
UI
1 | |
Qt Application
1 | |
Algorithm
1 | |
1.3 实验数据与测试结果分析
原始数据序列生成算法使用时间种子的除留余数法,在数据规模为
| shell | heap | quick | merge | |
|---|---|---|---|---|
| 1 | 129419 | 231824 | 39061 | 120488 |
| 2 | 128051 | 232204 | 38723 | 120487 |
| 3 | 134873 | 231945 | 39052 | 120251 |
| 4 | 135719 | 232096 | 39158 | 120510 |
| 5 | 128821 | 232051 | 38747 | 120434 |
| average | 131376 | 232024 | 38948 | 120434 |
可以发现:在数据规模在
1.4 程序清单
/Src/Algorithm/sortAlgorithm.cpp:内核排序算法/Src/Forms/SortWidget.ui:ui 界面/Src/Headers/SortWidget.h:排序组件逻辑头文件/Src/Post/SortWidget.cpp:排序组件逻辑源文件/Src/Test/TestSort.cpp:程序测试文件
其中,除了 ui 界面使用 Qt Designer 设计师工具进行编写,其余文件均为与文件名同名的 C++ 类,便于维护与扩展
二、选做题
题三:扫描一个 C 源程序,利用两种方法统计该源程序中的关键字出现的频度,并比较各自查找的比较次数。
用 Hash 表存储源程序中出现的关键字,利用 Hash 查找技术统计该程序中的关键字出现的频度。用线性探测法解决 Hash 冲突。设 Hash 函数为 Hash(key) = [(key 的第一个字母序号) × 100 + (key 的最后一个字母序号)] % 41
用顺序表存储源程序中出现的关键字,利用二分查找技术统计该程序中的关键字出现的频度。
2.1 数据结构设计与算法思想
- 第一问:
首先用关键字序列构造哈希表,哈希函数使用题中所给,容易算出哈希表的最大容量为
25 × 100 + 40 25 \times 100+40 3000 3000 int: <string, int>的键值对形式,可以使用动态数组容器std::vector<std::pair>进行存储。其中键设为int可以使得对于一个int类型的哈希值进行O ( 1 ) O(1) <word, cnt>,即<std::string, int>然后对于文件中的每一个单词采用哈希搜索。利用哈希函数计算出每一个单词的哈希值,然后通过线性探测法进行搜索比对。关键在于如何解析出一个完整的单词,对于流读入的字符串(不包含空格、换行符、制表符等空白符),我们删除其中的符号后将剩余部分进行合并,之后进行异常处理,排除空串后进行哈希查找。查找次数包含成功和失败的比较次数
- 第二问:将关键字存储于顺序表中,排序后,利用二分查找技术进行搜索统计。查找次数包含成功和失败的比较次数
2.2 程序结构
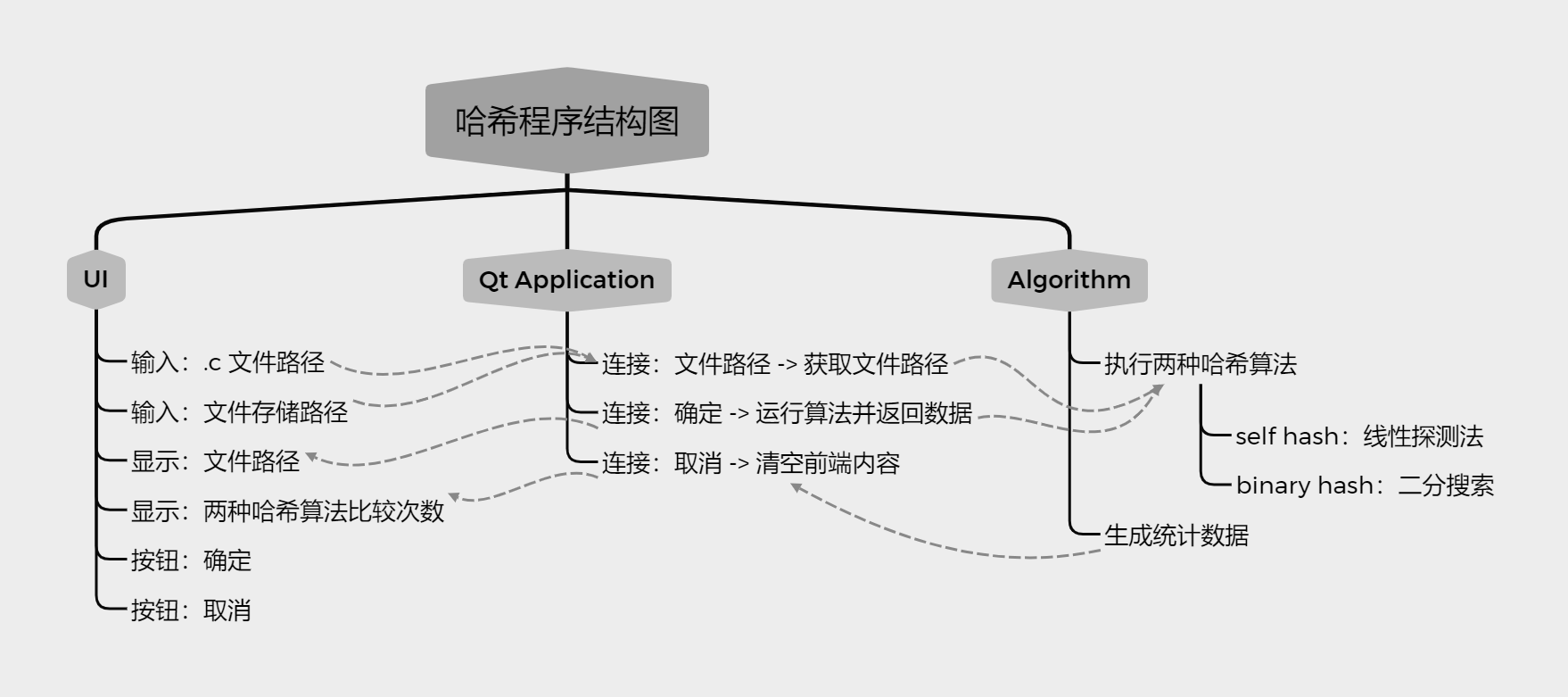
UI
1 | |
Qt Application
1 | |
Algorithm
1 | |
2.3 实验数据与测试结果分析
代码文件从 github 上下载而来,其中 100 行与 500 行的代码文件为完整程序,2500 行代码文件为手动构造程序,三种文件数据规模的查找比较次数如下:
| self hash | binary hash | |
|---|---|---|
| 100 lines | 120 | 775 |
| 500 lines | 1546 | 10300 |
| 2500 lines | 5561 | 39097 |
可以发现:使用线性探测法进行哈希的比较次数远小于二分搜索的比较次数
2.4 程序清单
/Src/Algorithm/hashAlgorithm.cpp:内核哈希算法/Src/Forms/HashWidget.ui:ui 界面/Src/Headers/HashWidget.h:哈希组件逻辑头文件/Src/Post/HashWidget.cpp:哈希组件逻辑源文件/Src/Test/TestHash.cpp:程序测试文件
其中,除了 ui 界面使用 Qt Designer 设计师工具进行编写,其余文件均为与文件名同名的 C++ 类,便于维护与扩展
三、收获与体会
算法思维。四种排序算法总共也就 100 行,加上堆排序采用树形迭代,快排与归并排序采用递归,整体编码难度并不算高。即使加上了文件 I/O 操作也不过 150 行。而第二道题也是 hash 查找与 binary 查找加上文件 I/O 操作,整体算法难度也十分有限。但是对于我来说也加强了 hash 构建与查找的逻辑。
前后端开发。为了锻炼设计模式思维与软件工程思维,我加入了 Qt 集成的 GUI 界面,不仅体会到了算法对于软件的核心作用所在,也体会到了窗口程序的数据交互与数据接口的开发过程。比如 Qt 中信号与槽的概念,其实就是一种数据交互的 API 格式。同时在体验开发过程的同时,也感受到了用户体验的前端板块,通过使用 Qt Designer 的设计师开发界面,可以通过拖动组件的形式进行可视化设计界面,提高了开发效率,如果可以多人组队,也实现了前后端分离的同步开发模式。
异常处理。与传统 OJ 不同的是,一个软件还需要考虑更多的异常处理,没有标准的 std 数据,加上用户输入、操作的无穷性,注定了软件的异常处理不是一个简单的事,比如在解析用户输入的字符串以及解析用户按钮操作的过程中,需要添加很多的字符串处理结构以及事件触发处理结构,这对于我强化软件开发的健壮性很有帮助。
版本管理。通过 Git 版本管理与 Github 的云端同步功能,也更能体会到开发留痕与 bug 检测的优势。
当然美中不足的也有很多,比如单人全栈开发并不利于锻炼团队协作的能力,同时对于程序的架构设计也没有经过深度考虑,仅仅有界面,数据正常交互就戛然而止。希望在未来的算法与开发路上可以走的更远、更坚定。
仓库地址
github: https://github.com/Explorer-Dong/DataStructureClassDesign
gitee: https://gitee.com/explorer-dong/DataStructureClassDesign
]]>第1章 行列式
1.1 二阶与三阶行列式
1.1.1 二元线性方程组与二阶行列所式
线性代数是为了解决多元线性方程组而诞生的
1.1.2 三阶行列式
记住对角线法则即可
1.2 全排列和对换
1.2.1 排列及其逆序数
排列:就是每个数位上数字的排序方式
逆序数:就是一个排列
1.2.2 对换
对换:就是排列中某两个数位之间的数字进行交换的操作
- 定理一:一个排列中两个元素对换,排列逆序数的奇偶性改变
- 推论:奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数
1.3 n阶行列式的定义
n阶行列式的值为
1.4 行列式的性质
性质一:行列式与它的转置行列式相等
性质二:对换行列式的两个行或者列,行列式变号
- 推论:若行列式有两行或两列完全相同,则行列式为零
性质三:行列式中若某一行(列)都乘以k,等于整个行列式的值乘以k
- 推论一:行列式的某一行(列)中的公因子可以提出到行列式之外
- 推论二:若行列式中有两行(列)成比例,则行列式的值为零
性质四:若行列式中某一行(列)都是两数之和,则可以拆分成两个行列式之和
性质五:把行列式中的某一行(列)乘以一个常数加到另一个行(列)上,行列式的值不变
技巧
- 计算技巧:在一开始对换行或者列的时候,尽可能保证左上角是数字1
- 所有的行(列)之和相等:先全部加到一行(列),再配凑上三角(下三角)
1.5 行列式按行(列)展开
余子式:
M i j M_{ij} 代数余子式:
A i j A_{ij} 关系:
A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij}
1.5.1 引理
一行(列)只有一个元素不为零,则
证明:
对于特殊情况,即不为零的元素在左上角,则根据上述分块矩阵,可知
D = ( − 1 ) 1 + 1 a i j M i j = a i j A i j D=(-1)^{1+1}a_{ij}M_{ij}=a_{ij}A_{ij} 对于一般情况,即某行(列)唯一不为零的元素在任意位置,则经过
i + j − 2 i+j-2 D = ( − 1 ) i + j − 2 a i j M i j = ( − 1 ) i + j a i j M i j = a i j A i j D=(-1)^{i+j-2}a_{ij}M_{ij}=(-1)^{i+j}a_{ij}M_{ij}=a_{ij}A_{ij}
1.5.2 定理
某行(列)(x)有多个元素不为零,则
证明:就是将展开的那一行(列)通过加法原理进行拆分,然后利用上述引理的一般情况进行证明即可
1.5.3 推论
对于上述的定理,讨论代数余子式前面的系数数组
如果系数数组不是第x行(列)的元素,而是其他行(列),那么上述Σ之和就为0
证明很简单,就是从原行列式出发,如果两行(列)元素完全一致,那么行列式显然为0
考点:
一般就是把不同行(列)的元素乘上其他行(列)的元素,然后适当配凑即可
几种特殊的行列式(补)
分块行列式
0 在左下或右上就是左上角与右下角行列式之积(
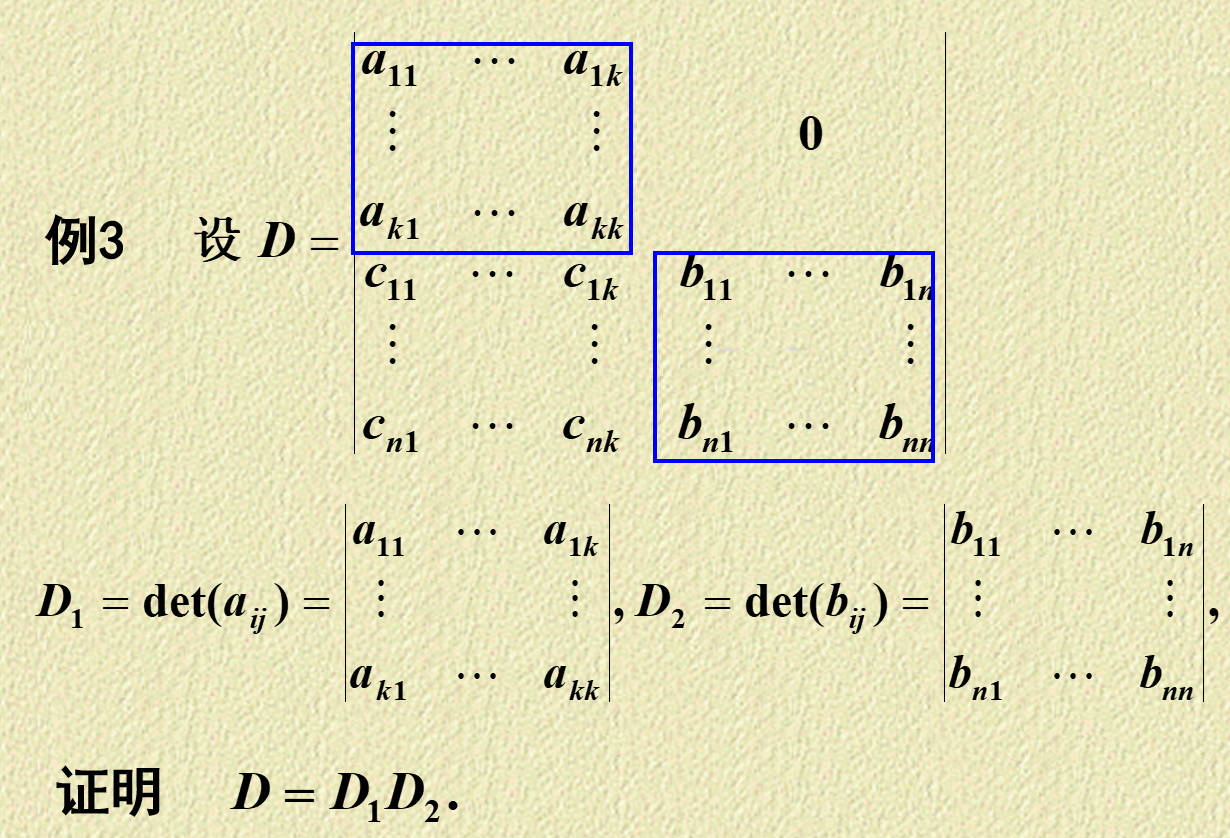
证明:分区域转换为上三角即可
2n 阶行列式
先行对换,再列对换,通过分块行列式和数学归纳法,可得答案为一个等比数列
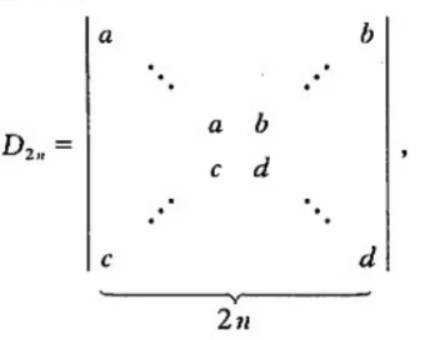
范德蒙德行列式 ⭐

证明:首先从最后一行开始,依次减去前一行的
第2章 矩阵及其运算
2.1 线性方程组和矩阵
2.1.1 线性方程组
把线性方程组中的数据搬到了矩阵中而已
2.1.2 矩阵的定义
相较于行列式是一个数,矩阵就是一个数表
- n阶矩阵
- 行(列)矩阵
- 零矩阵
- 对角矩阵:
Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ n ) \Lambda=diag(\lambda_1,\lambda_2,\cdots,\lambda_n) - 单位矩阵: 即主对角线全1,其余全0
- 线性变换:
y = x 1 + x 2 . . . y = x_1 + x_2 ...
2.2 矩阵的运算
2.2.1 矩阵的加法
按元素一个一个加
2.2.2 数与矩阵相乘
按元素一个一个乘
2.2.3 矩阵与矩阵相乘
- 基本规则:
A B = C AB=C c i j c_{ij} - 没有交换律:
A B AB - 有结合律、分配率
- 单位矩阵:主对角线上元素全为1,其余全为0
- 纯量矩阵:主对角线上元素全为
λ \lambda - 幂运算:当A、B两个方阵可交换时,有幂运算规律(因为有结合律)
矩阵乘法算律:

2.2.4 矩阵的转置
矩阵转置算律:

证明 (4):左边的
对称矩阵:对于一个方阵 A,如果

2.2.5 方阵的行列式
行列式算律:
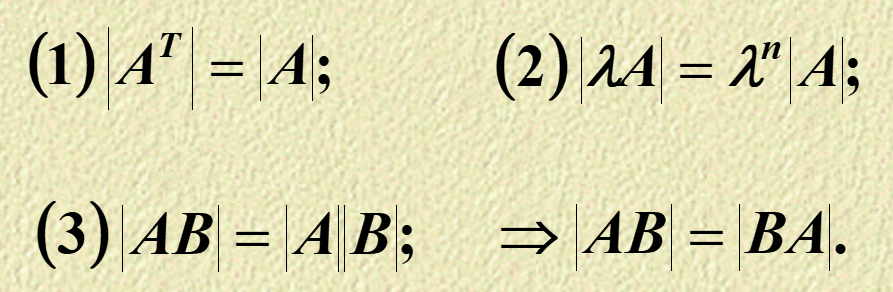
伴随矩阵:

2.3 逆矩阵
2.3.1 逆矩阵的定义、性质、求法
定义:
- 如果对于矩阵 A,有
A B = B A = E AB = BA = E
性质:
唯一性:如果矩阵 A 可逆,则 A 的逆矩阵是唯一的
行列式:如果矩阵A可逆,则
∣ A ∣ ≠ 0 |A| \ne 0 奇异矩阵:
∣ A ∣ = 0 |A| = 0 ∣ A ∣ ≠ 0 |A| \ne 0 必要条件:若
A B = E AB=E B A = E BA = E B = A − 1 B = A^{-1}
求法:
- 若
∣ A ∣ ≠ 0 |A| \ne 0 A − 1 = 1 ∣ A ∣ A ∗ A^{-1} = \frac{1}{|A|}A^*
逆矩阵算律:
2.3.2 逆矩阵的初步应用
(一)求逆矩阵:
(二)矩阵多项式:
定义:
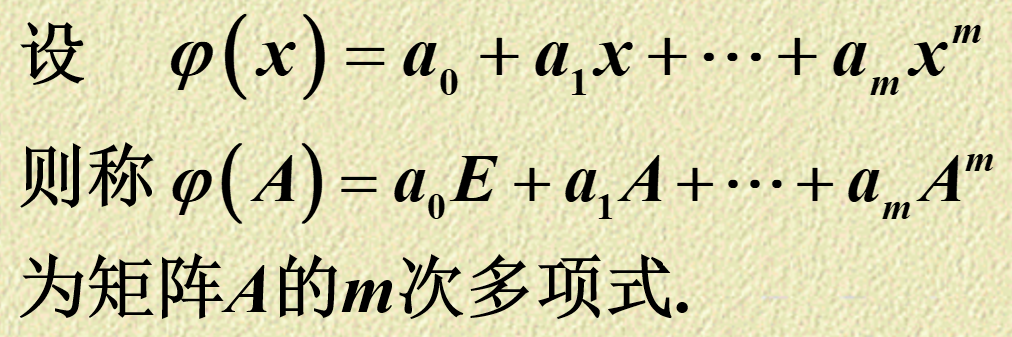
计算技巧一:直接代入
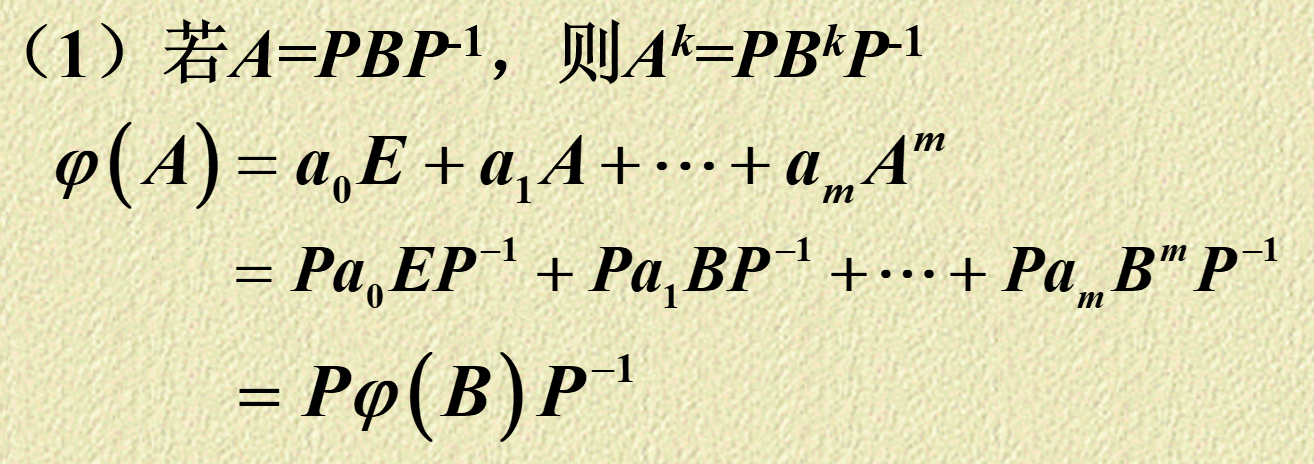
计算技巧二:对角阵幂运算
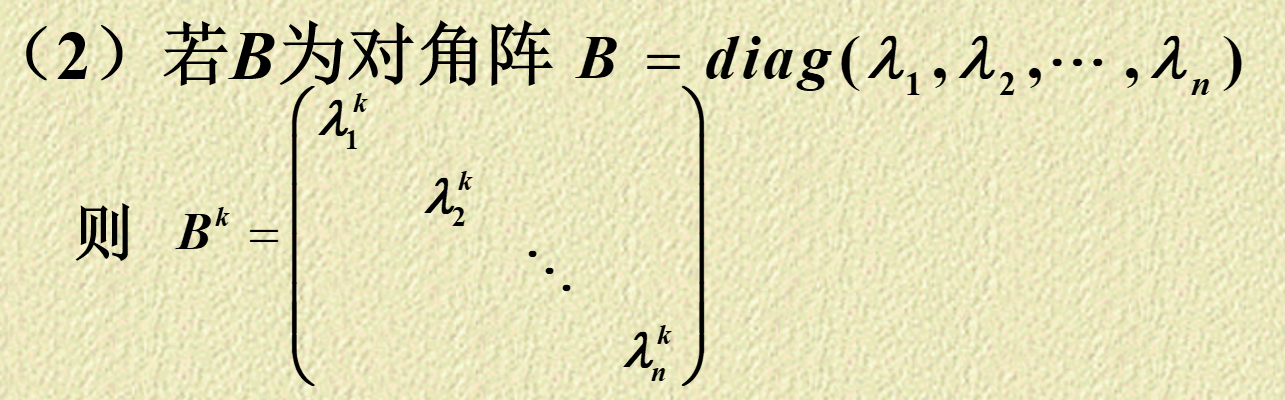
计算技巧三:对角矩阵多项式转化为数的多项式计算
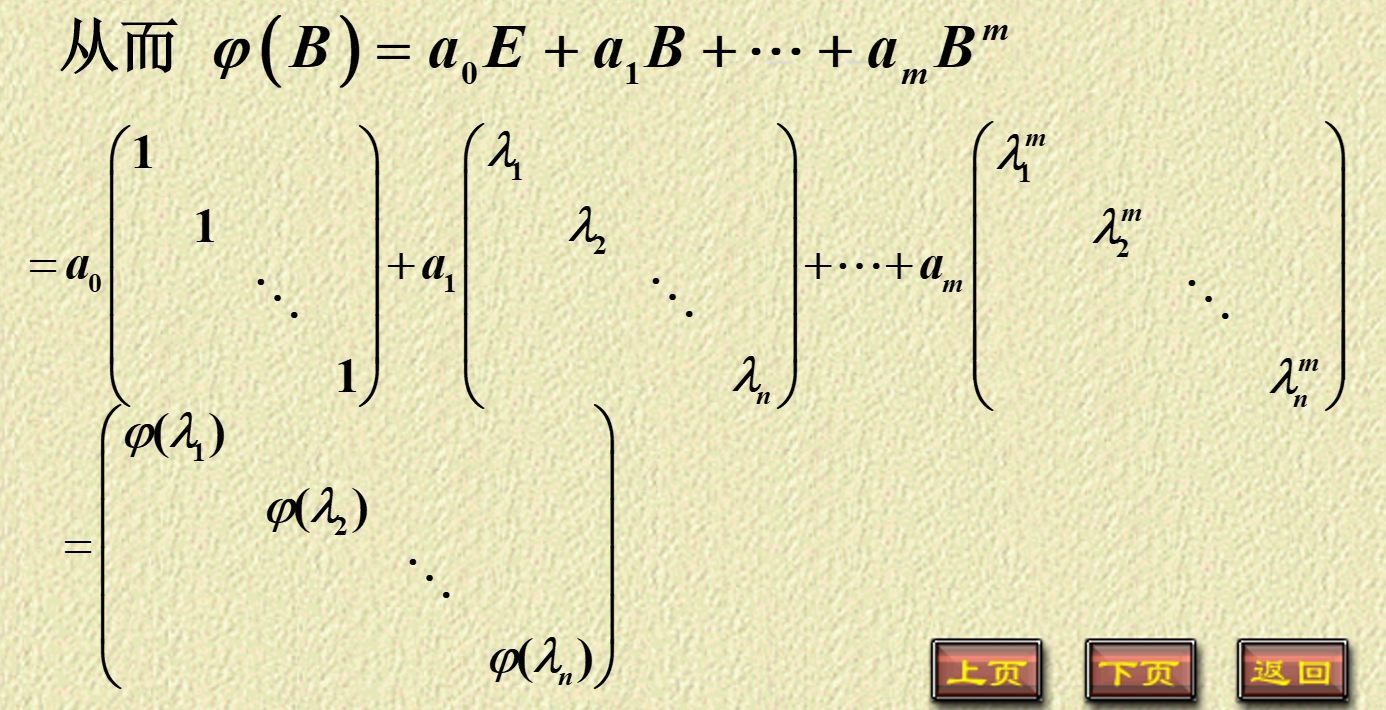
2.4 克拉默法则
应用:
求解未知数数量和方程个数相等,且系数行列式不为零的线性方程组
是求解一般线性方程组的一个特殊场景
结论:
如果线性方程组
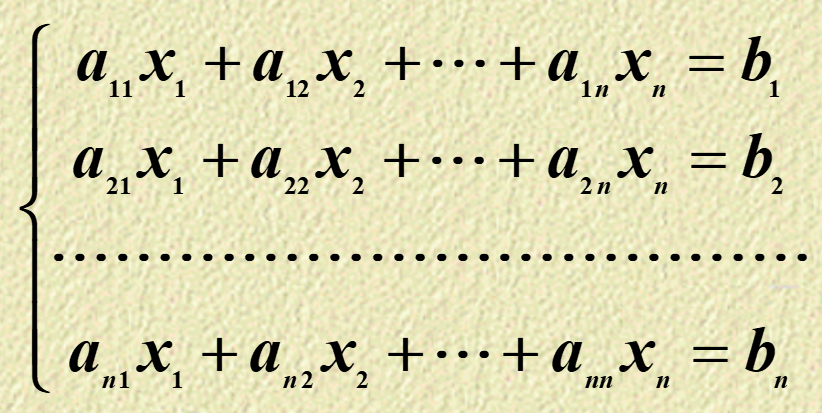
的系数矩阵 A 的行列式不为零,即

则方程组有唯一解
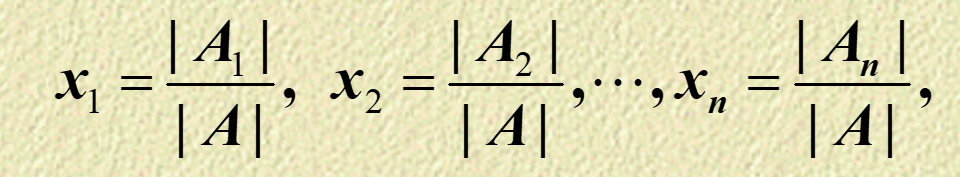
其中
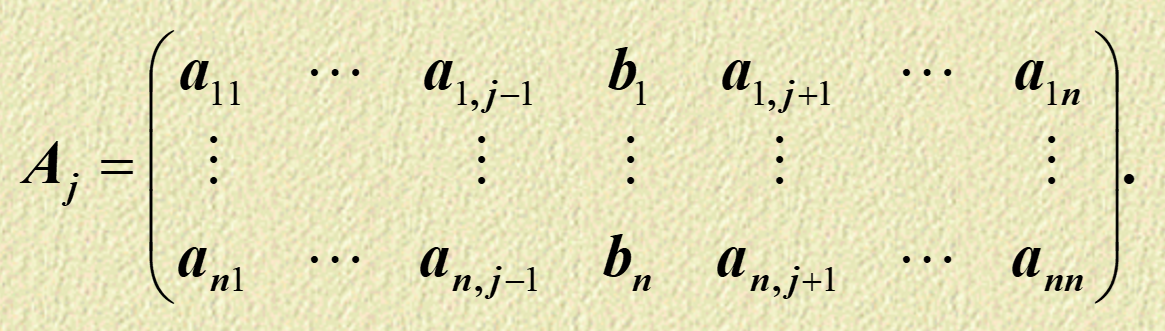
证明:
第一步:方程组转化为矩阵方程

第二步:应用逆矩阵消元

第三步:应用行列式的性质计算
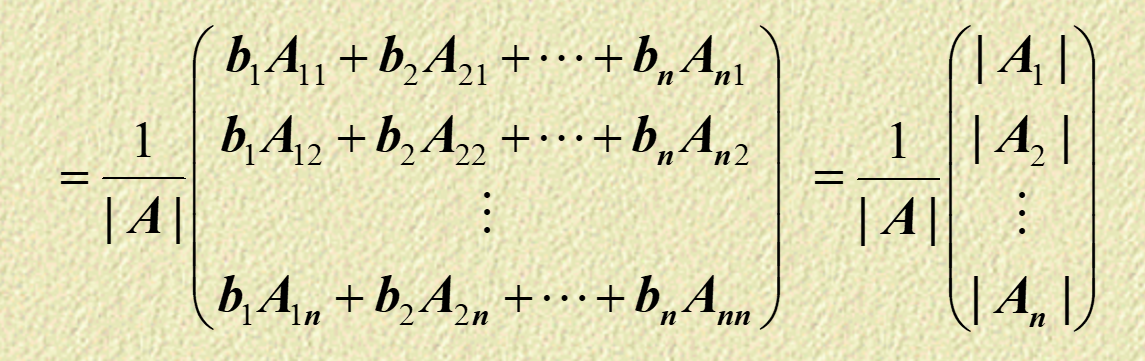
2.5 矩阵分块法
个人感觉就是一种向量化的更高级的思维,对于一个向量,进行全新向量的拆解,从而实现拆分计算。以下是 5 个拆分规则,重点关注第 5 点,即分块对角矩阵以及最后的按行按列分块的两个应用。
2.5.1 拆分规则
首先需要知道的是,在对矩阵进行分块计算的时候,前提有两个:一个是两个矩阵一开始的规格要相同,另一个是两个矩阵分块之后的规格也要相同。
按位加:
若
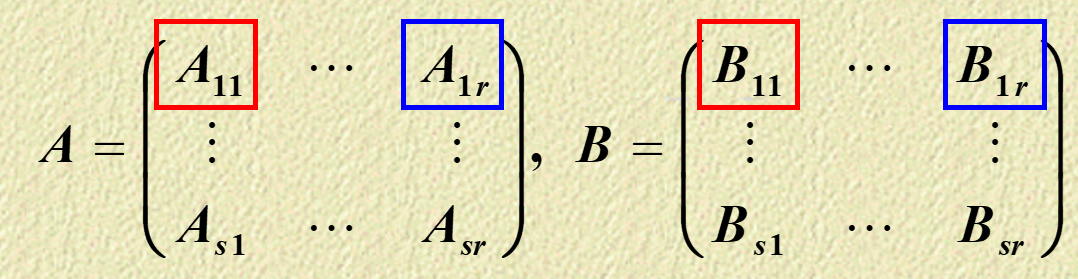
则

按位数乘:
若
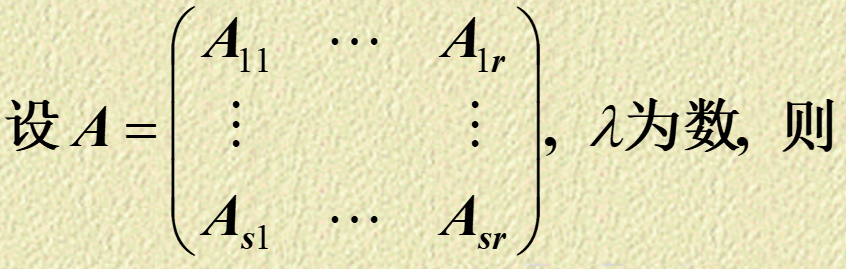
则
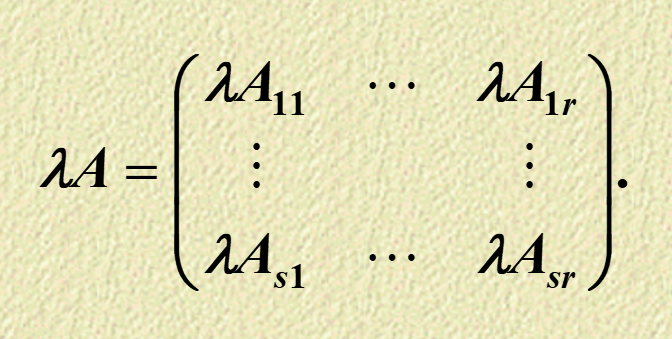
矩阵乘法:
若

则

其中
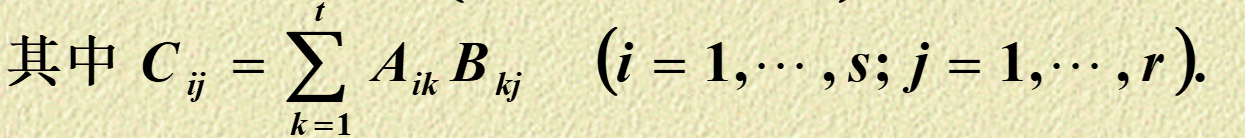
按位转置:
若

则
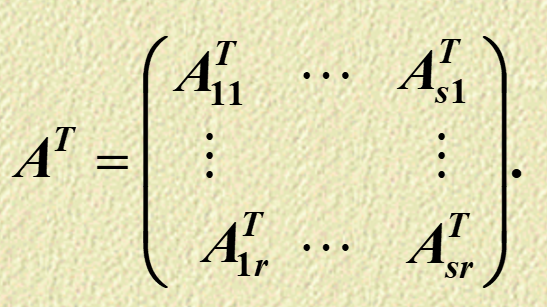
对角分块矩阵:

其中
2.5.2 运算性质
幂运算就是主对角线相应元素的幂运算

矩阵行列式运算性质
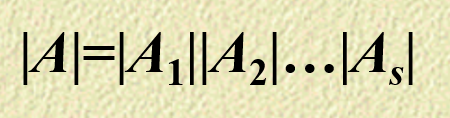
矩阵的逆就是主对角线的块按位取逆

按行按列分块的应用
A T A = O A^T A=O A = O A=O - 线性方程组的三种表示方式:
- 就是类似于一开始的矩阵数表的表示方式
- 将系数表示为一个矩阵,将未知数表示成一个矩阵,将常数项也表示成一个矩阵
- 同上,只是未知数保持不变,即
x 1 a 1 + x 2 a 2 + ⋯ + x n a 3 = b x_1 {a_1} + x_2 {a_2} + \cdots + x_n {a_3} = {b}
- 线性方程组的解的两种表示方式:
- 一一表示
- 列向量表示
2.5.3 好题举例
分块的整体运算思想 + 矩阵提取公因子

逆矩阵的按定义的求法,即配凑求出逆矩阵(常规计算法是利用了伴随矩阵的计算思想)
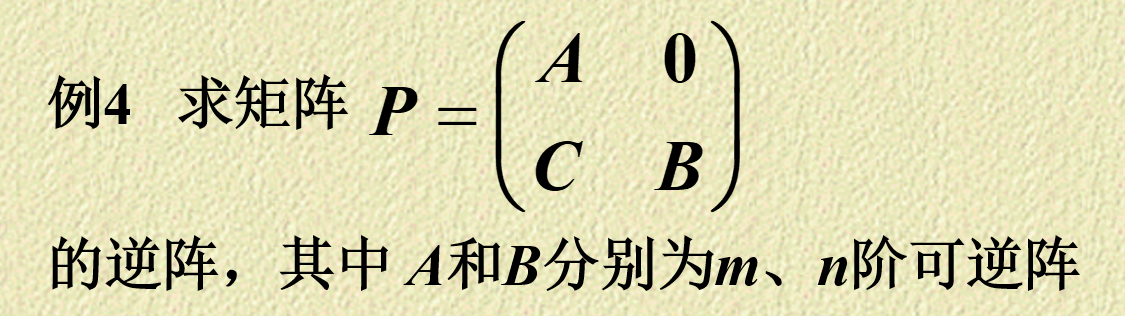
第3章 矩阵的初等变换与线性方程组
3.1 矩阵的初等变换
3.1.1 引入
矩阵的变换
3.1.2 矩阵的初等行变换
定义:
r i ↔ r j r_i \leftrightarrow r_j r i ← r i × k ( k ≠ 0 ) r_i \leftarrow r_i \times k\ (k \neq 0) r i ← r i + k r j r_i \leftarrow r_i + kr_j
性质:
- 将行变为列,就是矩阵的初等列变换
- 初等行变换与初等列变化统称初等变换
- 三种变换都是可逆的
3.1.3 矩阵的等价关系
定义:
A A B B A A B B A ∼ r B A \stackrel{r}{\sim} B A A B B A A B B A ∼ c B A \stackrel{c}{\sim} B A A B B A A B B A ∼ B A \sim B
性质:
- 反身性:
A ∼ A A \sim A - 对称性:若
A ∼ B \ A \sim B B ∼ A \ B \sim A - 传递性:若
A ∼ B \ A \sim B B ∼ C B \sim C A ∼ C \ A \sim C
3.1.3 三种形式的矩阵
行阶梯型矩阵

行最简形矩阵

标准形


3.1.4 性质1:矩阵初等变换的性质
对
A m × n A_{m\times n} A A m m 对
A m × n A_{m\times n} A A n n
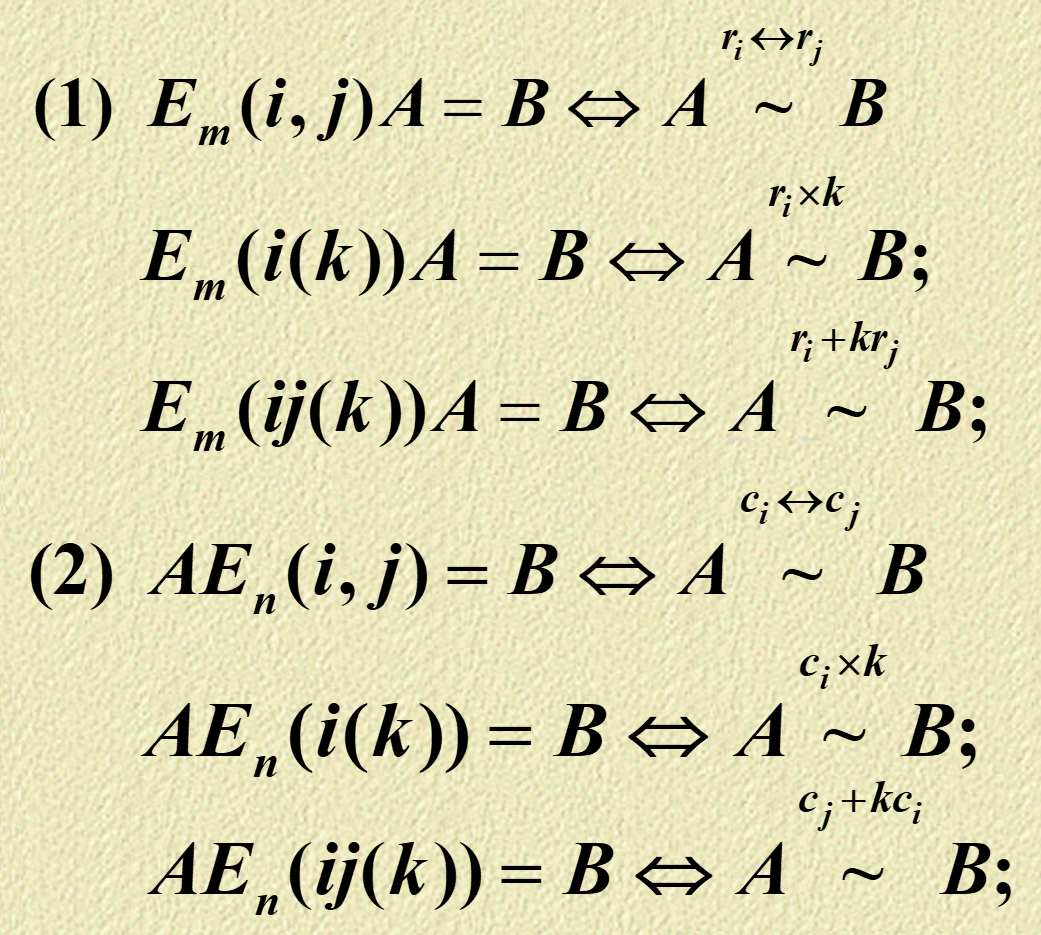
其中:
E m ( i , j ) E_m(i,j) i i j j E m ( i ( k ) ) E_m(i(k)) i i k k E m ( i j ( k ) ) E_m(ij(k)) i i j j k k
3.1.5 性质2:可逆的充要条件

3.1.6 定理:矩阵初等变换的存在性定理

对于(1)计算

3.1.7 推论:方阵可逆的等价推导

于是证明一个方阵
对于(1)当

3.1.8 初等变换的应用
(一)解方程
问题:已知矩阵
思路:首先需要证明
答案:最终的目标就是将拼接后的矩阵转化为行最简形矩阵,左边是一个单位矩阵即可
(二)解线性方程组
问题:求解方程数量和未知数数量一致的线性方程组
思路:同上方解方程的思路
补充:解这种线性方程组的策略:
- 高中学的:消元
- 第二章第 3 目:求
A − 1 b A^{-1}b - 第二章第 4 目:克拉默法则
- 上面刚学的:线性变换
3.2 矩阵的秩
定义:矩阵的非零子式的最高阶数,记作
性质:
转置不变性:
R ( A T ) = R ( A ) R(A^T)=R(A) 相似不变性:若 $A \sim B $,则
R ( A ) = R ( B ) R(A)=R(B) 初等变换不变性:若
P , Q P,Q R ( P A Q ) = R ( A ) R(PAQ)=R(A) 乘法性质:
0 ≤ R ( A m × n ) ≤ min { m , n } 0 \le R(A_{m\times n}) \le \min \{m, n\} 加法性质:
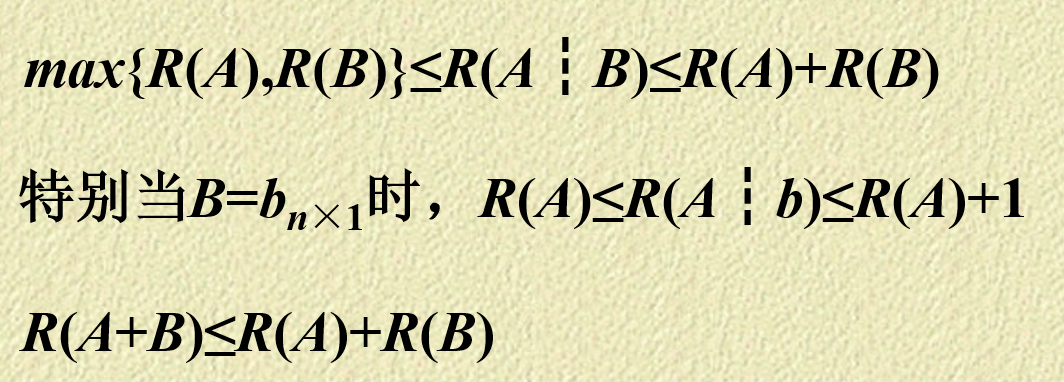
压缩性:若
A m × n A_{m\times n} r r A A [ E r O O O ] \begin{bmatrix}E_r & O \\O & O\end{bmatrix}
3.3 线性方程组的解
求解策略:利用 矩阵的初等变换 和 矩阵的秩 求解一般的线性方程组
对于
- 无解的充要条件:
R ( A ) < R ( A , b ) R(A)<R(A,b) - 有唯一解的充要条件:
R ( A ) = R ( A , b ) = n R(A)=R(A,b)=n - 有无限多解的充要条件:
R ( A ) = R ( A , b ) < n R(A)=R(A,b)<n
求解齐次线性方程组:
- 化简为行最简 or 行阶梯
求解非齐次线性方程组:
- 化简为行最简 or 行阶梯
第4章 向量组的线性相关性
4.1 向量组及其线性组合
4.1.1 n维向量的概念
显然的
向量组与矩阵的关系:
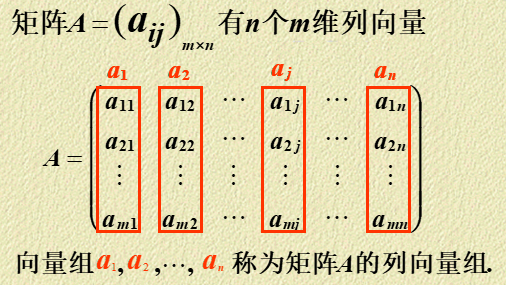
4.1.2 线性组合和线性表示
定义:
(一)线性组合:

(二)线性表示:

判定:转化为判定方程组有解问题,从而转化为求解矩阵的秩的问题 5
判定向量
b b A A 
判定向量组
B B A A 
该判定定理有以下推论:

判定向量组
B B A A 
4.2 向量组的线性相关性
定义:


判定:
定理一:

证明:按照定义,只需要移项 or 同除,进行构造即可
定理二:

证明:按照定义,转化为齐次线性方程组解的问题
- 有非零解
⇔ \Leftrightarrow R ( A ) = R ( A , 0 ) < m R(A)=R(A,0)<m - 仅有零解
⇔ \Leftrightarrow R ( A ) = R ( A , 0 ) = m R(A)=R(A,0)=m
- 有非零解
结论:
结论一:
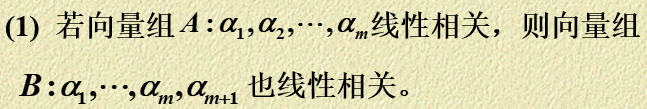
证明:
R ( A ) < m → R ( B ) ≤ R ( A ) + 1 < m + 1 R(A)<m \to R(B)\le R(A)+1 <m+1 结论二:

证明:
R ( A x × m ) = m → R ( A b ) = m R(A_{x\times m})=m \to R\binom{A}{b}=m 结论三:

证明:
R ( A ) ≤ n < m R(A)\le n <m 结论四:

证明:
R ( A ) = m , R ( A , b ) < m + 1 → A x = b 有唯一解 R(A)=m,R(A,b)<m+1 \to Ax=b\text{有唯一解} max { R ( A ) , R ( b ) } ≤ R ( A , b ) ≤ m + 1 → m ≤ R ( A , b ) ≤ m + 1 \max \{ R(A),R(b) \} \le R(A,b) \le m+1 \to m \le R(A,b) \le m+1 - 又
R ( A , b ) < m + 1 R(A,b)<m+1 - 故
R ( A , b ) = m R(A,b)=m - 因此
R ( A ) = R ( A , b ) = m → 有唯一解 R(A)=R(A,b)=m \to \text{有唯一解}
4.3 向量组的秩
4.3.1 最大无关组的定义
定义一:

注意:
- 最大无关组之间等价
- 最大无关组
A 0 A_0 A A
定义二:

4.3.2 向量组的秩和矩阵的秩的关系

4.3.3 向量组的秩的结论


证明:全部可以使用矩阵的秩的性质进行证明
4.4 向量空间
4.4.1 向量空间的概念
可以从高中学到的平面向量以及空间向量入手进行理解,即平面向量就是一个二维向量空间,同理空间向量就是一个三维向量空间,那么次数就是拓展到 n 维向量空间,道理是一样的,只不过超过三维之后就没有直观的效果展示罢了。
4.4.2 向量空间的基与维数
同样可以从高中学到的向量入手,此处的基就是基底,维数就是有几个基底。所有的基之间都是线性无关的,这是显然的。然后整个向量空间中任意一个向量都可以被基线性表示,也就很显然了,此处有三个考点,分别为:
考点一:求解空间中的某向量 x 在基 A 下的坐标
其实就是求解向量 x 在基 A 的各个“轴”上的投影。我们定义列向量
考点二:求解过度矩阵 P
我们已知一个向量空间中的两个基分别为 A 和 B,若有矩阵 P 满足基变换公式:
考点三:已知空间中的某向量 x 在基 A 下坐标为

4.5 线性方程组的解的结构
本目其实就是 3.3 目的一个知识补充,具体的线性方程组求解方法与 3.3 目几乎完全一致,只不过通过解的结构将解的结构进行了划分从而看似有些不同。但是殊途同归,都是一个东西。下面介绍本目与 3.3 目不同的地方:
我们从 3.3 目可以知道,无论是齐次线性方程组还是非齐次线性方程组,求解步骤都是:将系数矩阵(非齐次就是增广矩阵)进行行等价变换,然后对得到的方程组进行相对应未知变量的赋值即可。区别在于:
解释:我们将
- 齐次线性方程组记为
A x = 0 Ax=0 η \eta A η = 0 A \eta = 0 - 非齐次线性方程组记为
A x = b Ax=b η ∗ \eta^* A η ∗ = b A\eta^*=b η \eta A η = 0 A\eta=0 A ( η ∗ + η ) = b A(\eta^*+\eta)=b η ∗ + η \eta^* + \eta
也就是说本目对 3.3 目的线性方程组的求解给出了进一步的结构上的解释,即非齐次线性方程组的解的结构是基于本身的一个特解与齐次的通解之上的,仅此而已。当然了,本目在介绍齐次线性方程组解的结构时还引入了一个新的定理:
该定理可以作为一些证明秩相等的证明题的切入点。若想要证明两个$ n$ 元矩阵
第5章 相似矩阵及二次型
5.1 向量的内积、长度及正交性
5.1.1 内积
即各个位置的数依次相乘。运算规律如下:

推导全部按照内积的定义来,肥肠煎蛋
5.1.2 长度
类似于模长,有以下性质:

n 维向量与 n 维向量间的夹角:
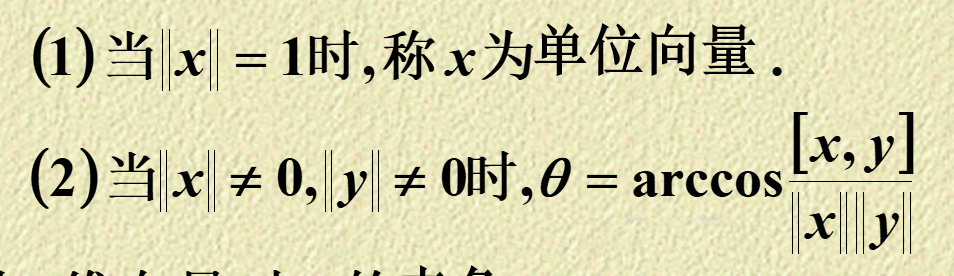
5.1.3 正交
类似于两个非零向量垂直的关系,即两向量内积为 0。
(一)正交向量组
- 定义:向量组之间的任意两两向量均正交
- 性质:正交向量组一定线性无关
(二)标准正交基
定义:是某空间向量的基+正交向量组+每一个向量都是单位向量
求解方法:施密特正交化
正交化:(其实就是对基础解系的一个线性组合)
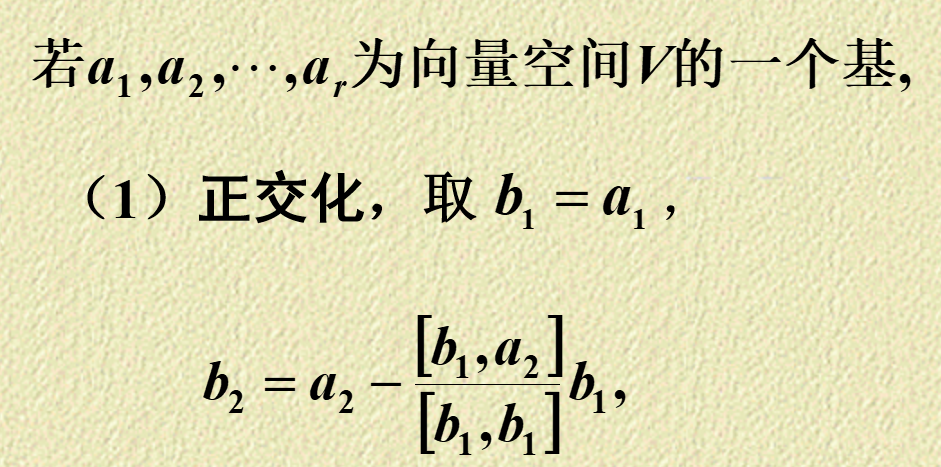
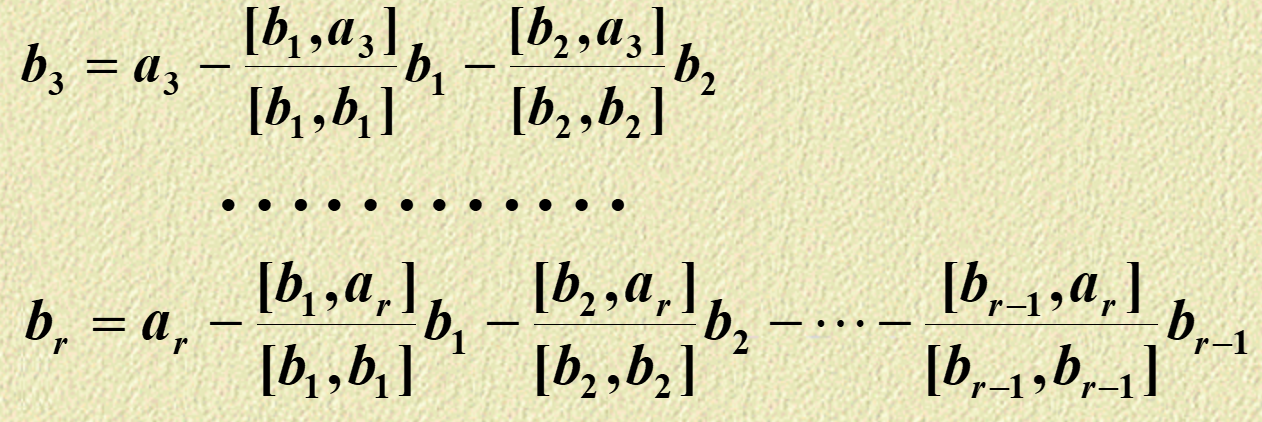
单位化:
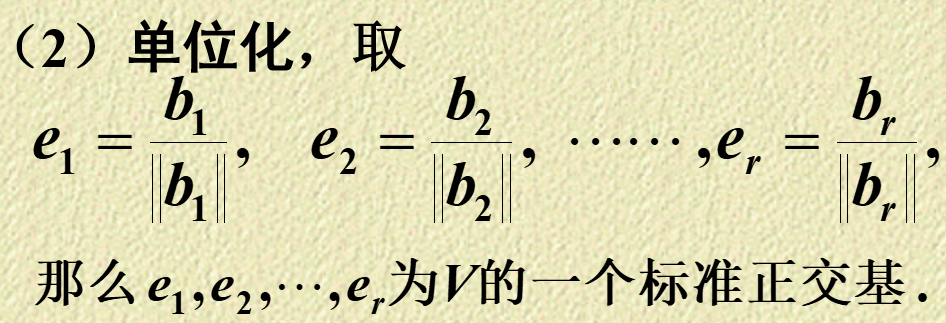
5.1.4 正交矩阵与正交变换
正交矩阵:(方阵)
- 定义:满足
A T A = E or A A T = E A^TA=E\ \text{or} \ AA^T=E - 定理:正交矩阵的充要条件为矩阵的行(列)向量为单位向量且两两正交
正交变换:
- 定义:对于正交矩阵
A A y = A x y=Ax - 性质:
∣ ∣ y ∣ ∣ = y T y = x T A T A x = x T E x = x T x = ∣ ∣ x ∣ ∣ ||y||=\sqrt{y^Ty}=\sqrt{x^TA^TAx}=\sqrt{x^TEx}=\sqrt{x^Tx}=||x||
5.2 方阵的特征值与特征向量
5.2.1 定义
对于一个n阶方阵 A,存在一个复数
则称 x 为特征向量,
5.2.2 特征值的性质
性质一
n阶矩阵 A 在复数范围内含有 n 个特征值,且
性质二
若
5.2.3 特征向量的性质
对于同一个矩阵,不同的特征值对应的特征向量之间是线性无关的
5.3 相似矩阵
5.3.1 定义
对于两个 n 阶方阵 A, B 而言,若存在可逆矩阵 P 使得
则称 B 为 A 的相似矩阵,A 与 B 相似,也称对 A 进行相似变换,P 为相似变换矩阵
5.3.2 性质
若矩阵 A 与 B 相似,则 A 与 B 的特征多项式相同,则 A 与 B 的特征值也就相同,A 与 B 的行列式也就相同
5.3.3 矩阵多项式
一个矩阵 A 的多项式
5.4 对称矩阵的对角化
本目讨论一个 n 阶方阵具备什么条件才能拥有 n 个线性无关的特征向量,从而可对角化。但是对于一般的方阵,情况过于复杂,此处只讨论 n 阶对称矩阵。即:一个 n 阶对角矩阵具备什么条件才能拥有 n 个线性无关的特征向量,从而可对角化。
答案是 n 阶对角矩阵一定是可对角化的。因为有一个定理是这样的:对于一个对称矩阵 A 而言,一定可以找到一个正交矩阵 P 使得
对称矩阵的性质
- 对称矩阵的特征值均为实数
- 对称矩阵 A 的两个特征值
λ 1 \lambda _1 λ 2 \lambda _2 P 1 P_1 P 2 P_2 λ 1 ≠ λ 2 \lambda_1 \ne \lambda_2 P 1 P_1 P 2 P_2 P 1 P_1 P 2 P_2 - 对称矩阵的每一个 k 重根,一定对应有 k 个线性无关的特征向量
因此本目相较于 5.3 目其实就是通过可对角化这一个概念,来告诉我们对称矩阵是一定可以求出对角矩阵的。而不用判断当前矩阵是否可对角化了。只不过在此基础之上还附加了一个小定理(也没给出证明),就是对称矩阵的相似变换矩阵一定是一个正交矩阵,那么也就复习回顾了 5.1 目中学到的正交矩阵的概念。为了求解出这个正交矩阵,我们需要在 5.3 目求解特征向量之后再加一个操作,即:对于一个 k 重根,根据上面的性质3我们知道当前的根一定有 k 个线性无关的特征向量,为了凑出最终的正交矩阵,我们需要对这 k 个线性无关的特征向量正交化。那么所有的特征值下的特征向量都正交化之后,又由性质2可知,不同的特征值下的特征向量又是正交的,于是最终的正交的相似变换矩阵也就求出来了,也就得到了对角矩阵
5.5 二次型及其标准型(部分)
本目只需要掌握到:将一个二次型转化为标准型,即可。其实就是比 5.4 目多一个将二次齐次函数的系数取出组成一个二次型的步骤。其中二次型就是一个对称矩阵。接着就是重复 5.4 目中的将对称矩阵转化为对角矩阵的过程了。
补
对称矩阵和正定性之间的关系
在最优化方法中我们需要通过目标函数海塞矩阵的正定性来判断凸性,显然的海塞矩阵是对称方阵。可以分别从特征值和行列式的角度进行判断。
特征值角度
- 一个对称矩阵 A 是正定的,当且仅当它的所有特征值
λ i > 0 \lambda_i>0 - 一个对称矩阵 A 是正半定的,当且仅当它的所有特征值
λ i ≥ 0 \lambda_i \ge 0
行列式角度
- 一个对称矩阵 A 是正定的,当且仅当所有主子矩阵的行列式都大于零
- 一个对称矩阵 A 是正半定的,当且仅当所有主子矩阵的行列式都大于或等于零
第1章 行列式
1.1 二阶与三阶行列式
1.1.1 二元线性方程组与二阶行列所式
线性代数是为了解决多元线性方程组而诞生的
1.1.2 三阶行列式
记住对角线法则即可
1.2 全排列和对换
1.2.1 排列及其逆序数
排列:就是每个数位上数字的排序方式
逆序数:就是一个排列
1.2.2 对换
对换:就是排列中某两个数位之间的数字进行交换的操作
- 定理一:一个排列中两个元素对换,排列逆序数的奇偶性改变
- 推论:奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数
1.3 n阶行列式的定义
n阶行列式的值为
1.4 行列式的性质
性质一:行列式与它的转置行列式相等
性质二:对换行列式的两个行或者列,行列式变号
- 推论:若行列式有两行或两列完全相同,则行列式为零
性质三:行列式中若某一行(列)都乘以k,等于整个行列式的值乘以k
- 推论一:行列式的某一行(列)中的公因子可以提出到行列式之外
- 推论二:若行列式中有两行(列)成比例,则行列式的值为零
性质四:若行列式中某一行(列)都是两数之和,则可以拆分成两个行列式之和
性质五:把行列式中的某一行(列)乘以一个常数加到另一个行(列)上,行列式的值不变
技巧
- 计算技巧:在一开始对换行或者列的时候,尽可能保证左上角是数字1
- 所有的行(列)之和相等:先全部加到一行(列),再配凑上三角(下三角)
1.5 行列式按行(列)展开
余子式:
M i j M_{ij} 代数余子式:
A i j A_{ij} 关系:
A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij}
1.5.1 引理
一行(列)只有一个元素不为零,则
证明:
对于特殊情况,即不为零的元素在左上角,则根据上述分块矩阵,可知
D = ( − 1 ) 1 + 1 a i j M i j = a i j A i j D=(-1)^{1+1}a_{ij}M_{ij}=a_{ij}A_{ij} 对于一般情况,即某行(列)唯一不为零的元素在任意位置,则经过
i + j − 2 i+j-2 D = ( − 1 ) i + j − 2 a i j M i j = ( − 1 ) i + j a i j M i j = a i j A i j D=(-1)^{i+j-2}a_{ij}M_{ij}=(-1)^{i+j}a_{ij}M_{ij}=a_{ij}A_{ij}
1.5.2 定理
某行(列)(x)有多个元素不为零,则
证明:就是将展开的那一行(列)通过加法原理进行拆分,然后利用上述引理的一般情况进行证明即可
1.5.3 推论
对于上述的定理,讨论代数余子式前面的系数数组
如果系数数组不是第x行(列)的元素,而是其他行(列),那么上述Σ之和就为0
证明很简单,就是从原行列式出发,如果两行(列)元素完全一致,那么行列式显然为0
考点:
一般就是把不同行(列)的元素乘上其他行(列)的元素,然后适当配凑即可
几种特殊的行列式(补)
分块行列式
0 在左下或右上就是左上角与右下角行列式之积(

证明:分区域转换为上三角即可
2n 阶行列式
先行对换,再列对换,通过分块行列式和数学归纳法,可得答案为一个等比数列

范德蒙德行列式 ⭐

证明:首先从最后一行开始,依次减去前一行的
第2章 矩阵及其运算
2.1 线性方程组和矩阵
2.1.1 线性方程组
把线性方程组中的数据搬到了矩阵中而已
2.1.2 矩阵的定义
相较于行列式是一个数,矩阵就是一个数表
- n阶矩阵
- 行(列)矩阵
- 零矩阵
- 对角矩阵:
Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ n ) \Lambda=diag(\lambda_1,\lambda_2,\cdots,\lambda_n) - 单位矩阵: 即主对角线全1,其余全0
- 线性变换:
y = x 1 + x 2 . . . y = x_1 + x_2 ...
2.2 矩阵的运算
2.2.1 矩阵的加法
按元素一个一个加
2.2.2 数与矩阵相乘
按元素一个一个乘
2.2.3 矩阵与矩阵相乘
- 基本规则:
A B = C AB=C c i j c_{ij} - 没有交换律:
A B AB - 有结合律、分配率
- 单位矩阵:主对角线上元素全为1,其余全为0
- 纯量矩阵:主对角线上元素全为
λ \lambda - 幂运算:当A、B两个方阵可交换时,有幂运算规律(因为有结合律)
矩阵乘法算律:

2.2.4 矩阵的转置
矩阵转置算律:

证明 (4):左边的
对称矩阵:对于一个方阵 A,如果

2.2.5 方阵的行列式
行列式算律:
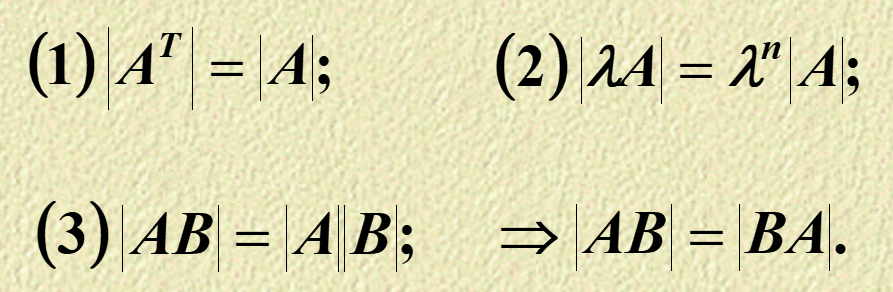
伴随矩阵:

2.3 逆矩阵
2.3.1 逆矩阵的定义、性质、求法
定义:
- 如果对于矩阵 A,有
A B = B A = E AB = BA = E
性质:
唯一性:如果矩阵 A 可逆,则 A 的逆矩阵是唯一的
行列式:如果矩阵A可逆,则
∣ A ∣ ≠ 0 |A| \ne 0 奇异矩阵:
∣ A ∣ = 0 |A| = 0 ∣ A ∣ ≠ 0 |A| \ne 0 必要条件:若
A B = E AB=E B A = E BA = E B = A − 1 B = A^{-1}
求法:
- 若
∣ A ∣ ≠ 0 |A| \ne 0 A − 1 = 1 ∣ A ∣ A ∗ A^{-1} = \frac{1}{|A|}A^*
逆矩阵算律:
2.3.2 逆矩阵的初步应用
(一)求逆矩阵:
(二)矩阵多项式:
定义:
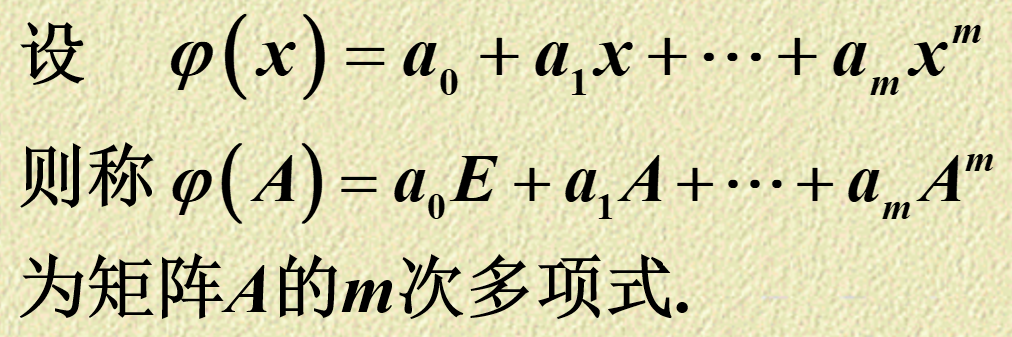
计算技巧一:直接代入
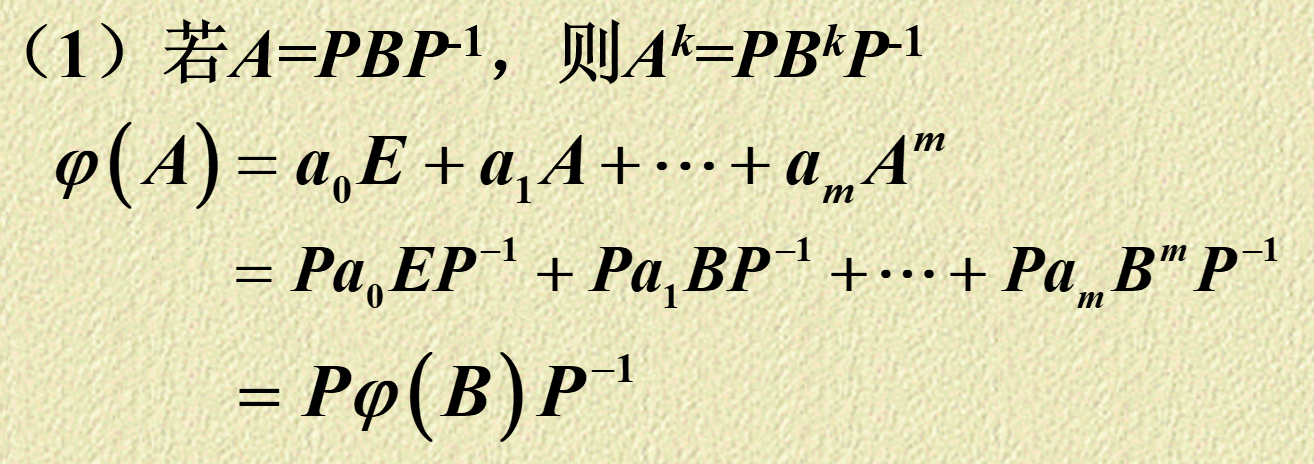
计算技巧二:对角阵幂运算
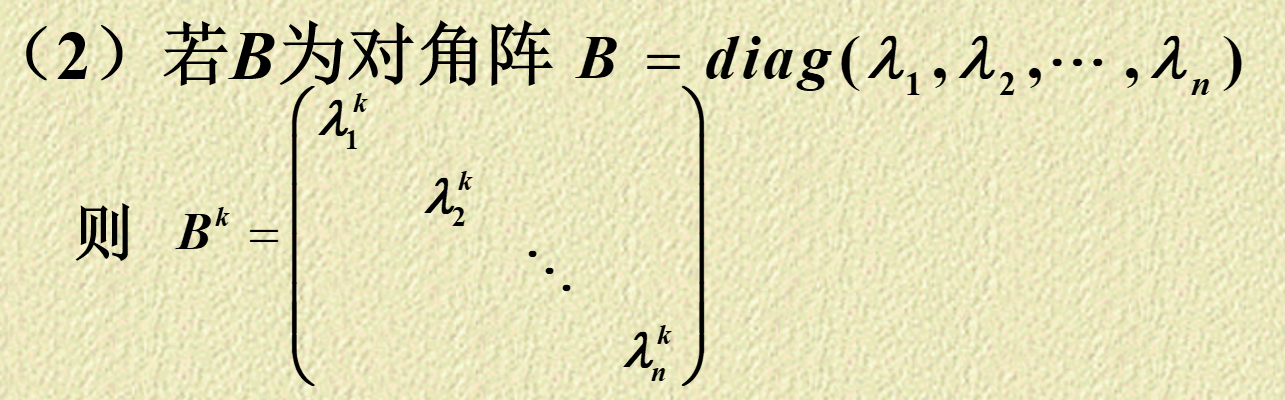
计算技巧三:对角矩阵多项式转化为数的多项式计算
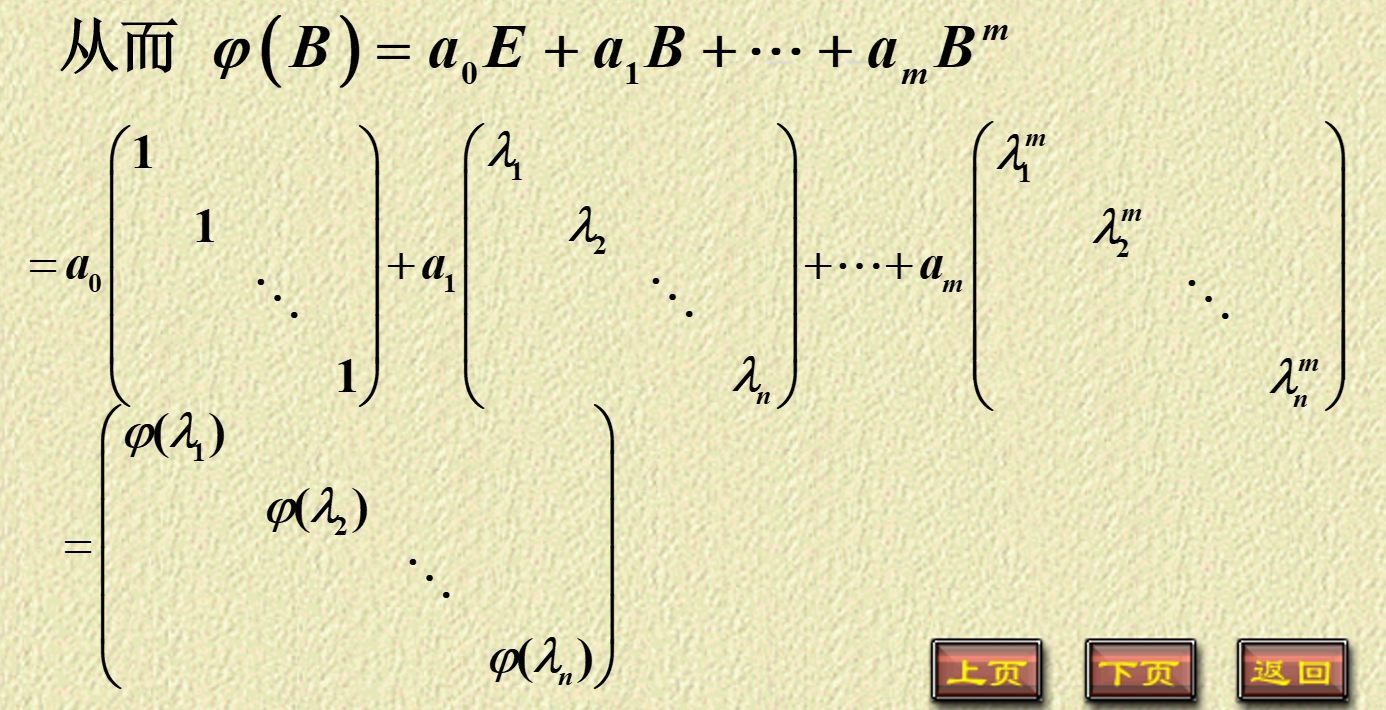
2.4 克拉默法则
应用:
求解未知数数量和方程个数相等,且系数行列式不为零的线性方程组
是求解一般线性方程组的一个特殊场景
结论:
如果线性方程组
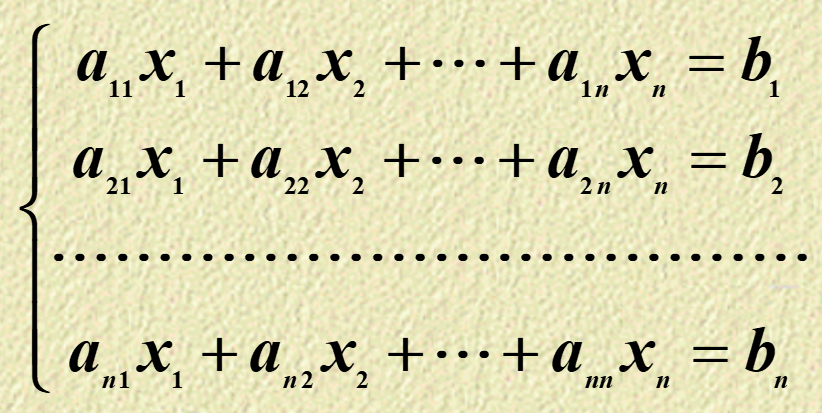
的系数矩阵 A 的行列式不为零,即

则方程组有唯一解
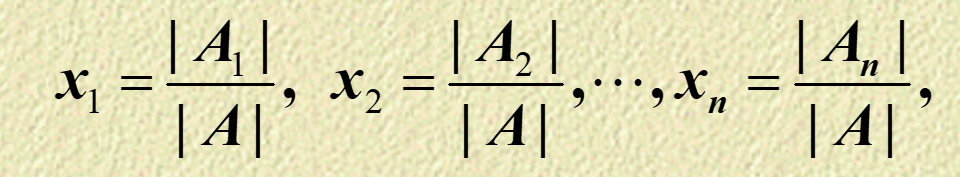
其中
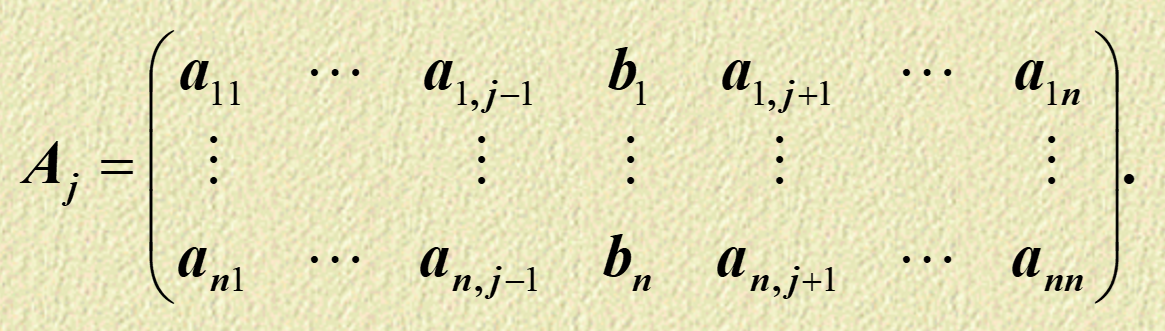
证明:
第一步:方程组转化为矩阵方程

第二步:应用逆矩阵消元

第三步:应用行列式的性质计算
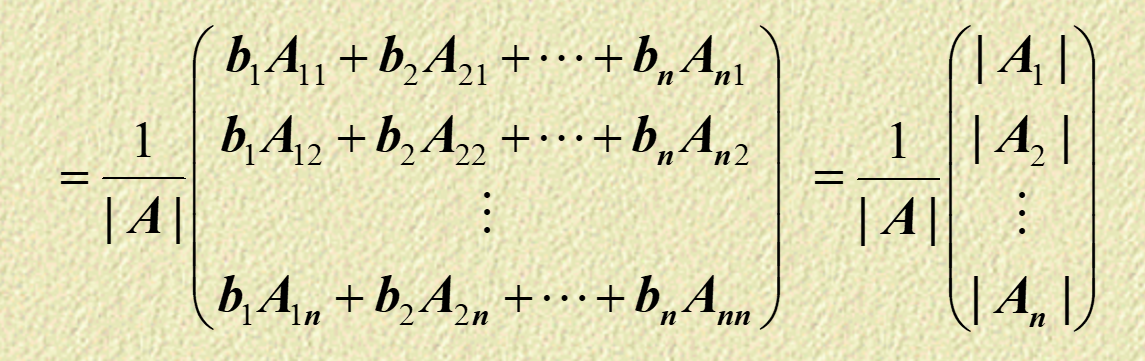
2.5 矩阵分块法
个人感觉就是一种向量化的更高级的思维,对于一个向量,进行全新向量的拆解,从而实现拆分计算。以下是 5 个拆分规则,重点关注第 5 点,即分块对角矩阵以及最后的按行按列分块的两个应用。
2.5.1 拆分规则
首先需要知道的是,在对矩阵进行分块计算的时候,前提有两个:一个是两个矩阵一开始的规格要相同,另一个是两个矩阵分块之后的规格也要相同。
按位加:
若
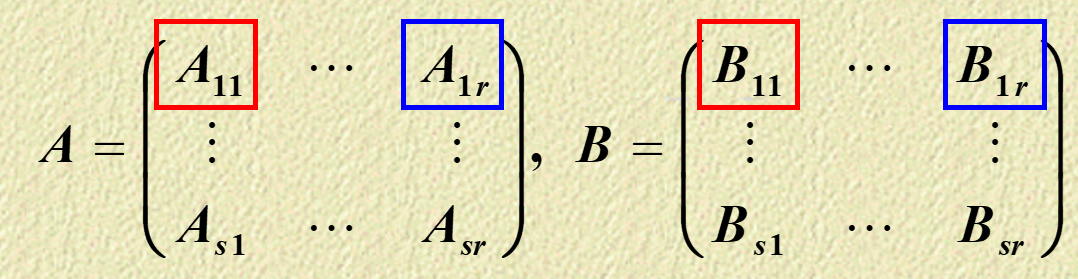
则

按位数乘:
若

则
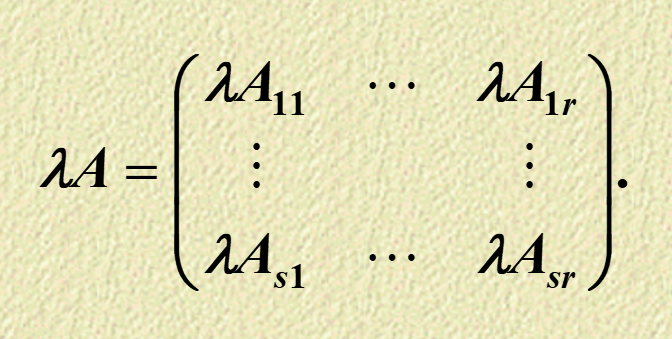
矩阵乘法:
若

则

其中
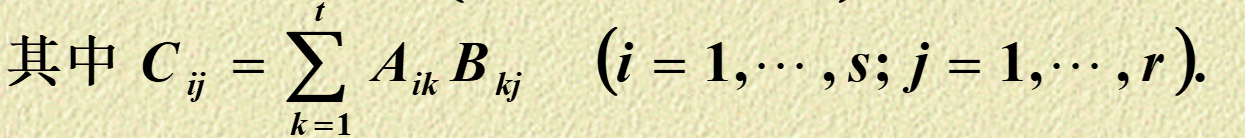
按位转置:
若

则
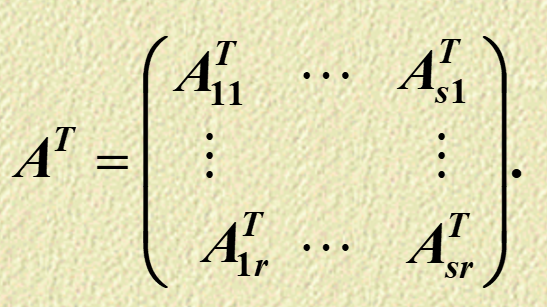
对角分块矩阵:

其中
2.5.2 运算性质
幂运算就是主对角线相应元素的幂运算

矩阵行列式运算性质
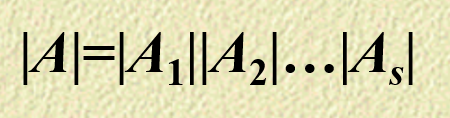
矩阵的逆就是主对角线的块按位取逆

按行按列分块的应用
A T A = O A^T A=O A = O A=O - 线性方程组的三种表示方式:
- 就是类似于一开始的矩阵数表的表示方式
- 将系数表示为一个矩阵,将未知数表示成一个矩阵,将常数项也表示成一个矩阵
- 同上,只是未知数保持不变,即
x 1 a 1 + x 2 a 2 + ⋯ + x n a 3 = b x_1 {a_1} + x_2 {a_2} + \cdots + x_n {a_3} = {b}
- 线性方程组的解的两种表示方式:
- 一一表示
- 列向量表示
2.5.3 好题举例
分块的整体运算思想 + 矩阵提取公因子

逆矩阵的按定义的求法,即配凑求出逆矩阵(常规计算法是利用了伴随矩阵的计算思想)
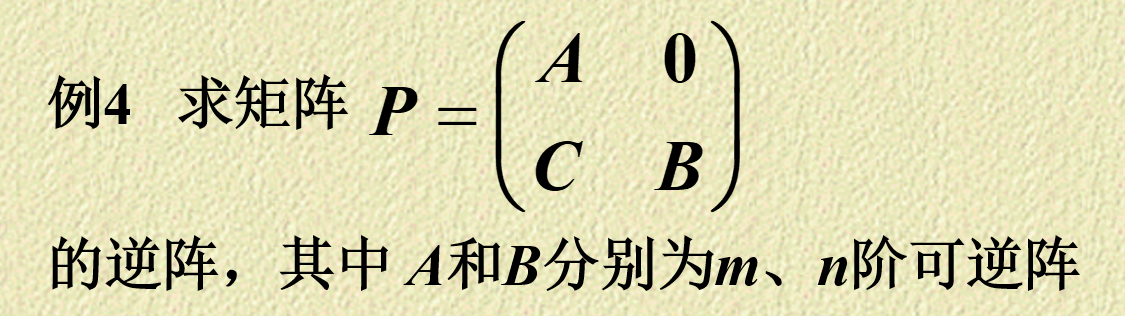
第3章 矩阵的初等变换与线性方程组
3.1 矩阵的初等变换
3.1.1 引入
矩阵的变换
3.1.2 矩阵的初等行变换
定义:
r i ↔ r j r_i \leftrightarrow r_j r i ← r i × k ( k ≠ 0 ) r_i \leftarrow r_i \times k\ (k \neq 0) r i ← r i + k r j r_i \leftarrow r_i + kr_j
性质:
- 将行变为列,就是矩阵的初等列变换
- 初等行变换与初等列变化统称初等变换
- 三种变换都是可逆的
3.1.3 矩阵的等价关系
定义:
A A B B A A B B A ∼ r B A \stackrel{r}{\sim} B A A B B A A B B A ∼ c B A \stackrel{c}{\sim} B A A B B A A B B A ∼ B A \sim B
性质:
- 反身性:
A ∼ A A \sim A - 对称性:若
A ∼ B \ A \sim B B ∼ A \ B \sim A - 传递性:若
A ∼ B \ A \sim B B ∼ C B \sim C A ∼ C \ A \sim C
3.1.3 三种形式的矩阵
行阶梯型矩阵

行最简形矩阵

标准形


3.1.4 性质1:矩阵初等变换的性质
对
A m × n A_{m\times n} A A m m 对
A m × n A_{m\times n} A A n n
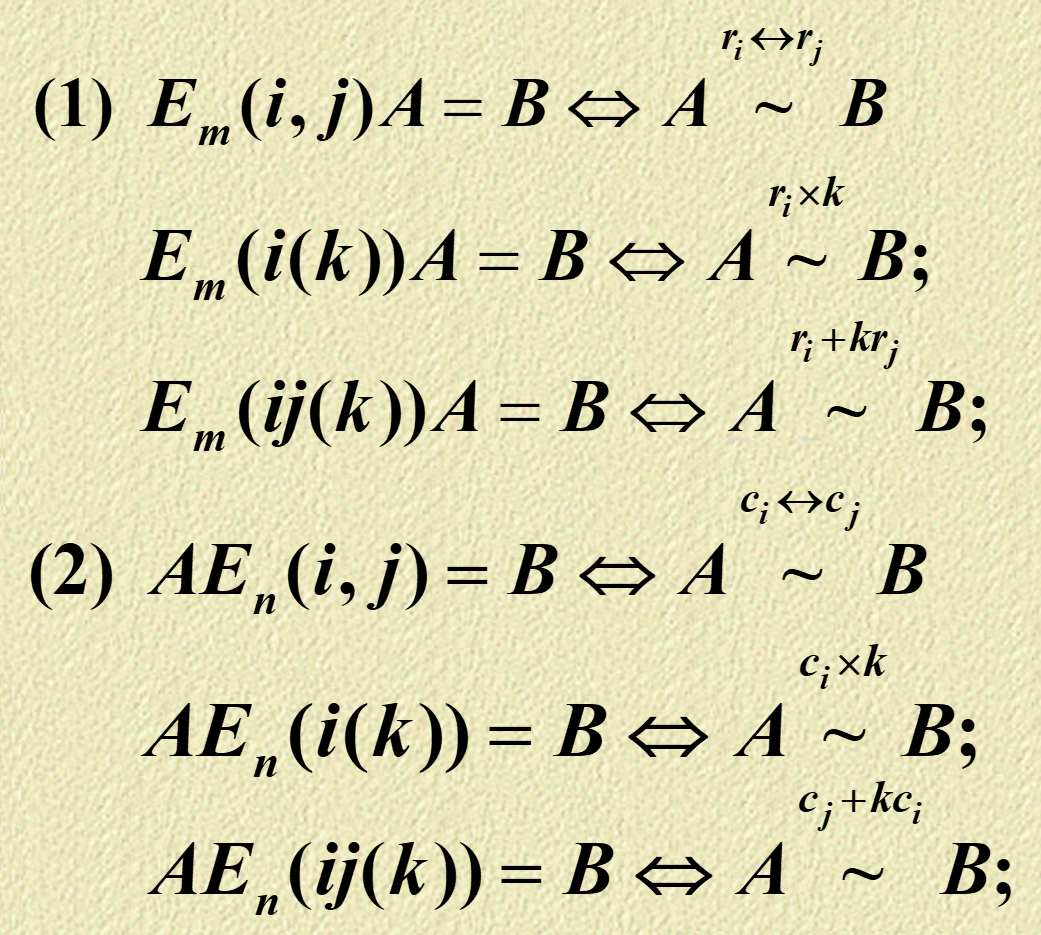
其中:
E m ( i , j ) E_m(i,j) i i j j E m ( i ( k ) ) E_m(i(k)) i i k k E m ( i j ( k ) ) E_m(ij(k)) i i j j k k
3.1.5 性质2:可逆的充要条件

3.1.6 定理:矩阵初等变换的存在性定理

对于(1)计算

3.1.7 推论:方阵可逆的等价推导

于是证明一个方阵
对于(1)当

3.1.8 初等变换的应用
(一)解方程
问题:已知矩阵
思路:首先需要证明
答案:最终的目标就是将拼接后的矩阵转化为行最简形矩阵,左边是一个单位矩阵即可
(二)解线性方程组
问题:求解方程数量和未知数数量一致的线性方程组
思路:同上方解方程的思路
补充:解这种线性方程组的策略:
- 高中学的:消元
- 第二章第 3 目:求
A − 1 b A^{-1}b - 第二章第 4 目:克拉默法则
- 上面刚学的:线性变换
3.2 矩阵的秩
定义:矩阵的非零子式的最高阶数,记作
性质:
转置不变性:
R ( A T ) = R ( A ) R(A^T)=R(A) 相似不变性:若 $A \sim B $,则
R ( A ) = R ( B ) R(A)=R(B) 初等变换不变性:若
P , Q P,Q R ( P A Q ) = R ( A ) R(PAQ)=R(A) 乘法性质:
0 ≤ R ( A m × n ) ≤ min { m , n } 0 \le R(A_{m\times n}) \le \min \{m, n\} 加法性质:
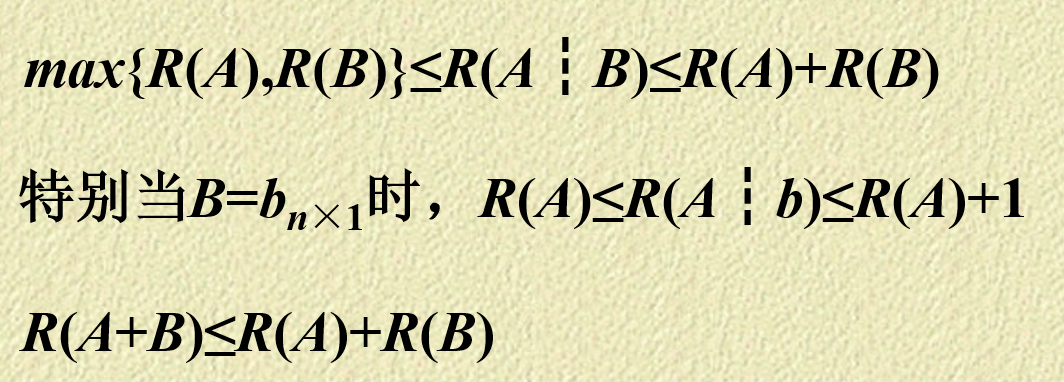
压缩性:若
A m × n A_{m\times n} r r A A [ E r O O O ] \begin{bmatrix}E_r & O \\O & O\end{bmatrix}
3.3 线性方程组的解
求解策略:利用 矩阵的初等变换 和 矩阵的秩 求解一般的线性方程组
对于
- 无解的充要条件:
R ( A ) < R ( A , b ) R(A)<R(A,b) - 有唯一解的充要条件:
R ( A ) = R ( A , b ) = n R(A)=R(A,b)=n - 有无限多解的充要条件:
R ( A ) = R ( A , b ) < n R(A)=R(A,b)<n
求解齐次线性方程组:
- 化简为行最简 or 行阶梯
求解非齐次线性方程组:
- 化简为行最简 or 行阶梯
第4章 向量组的线性相关性
4.1 向量组及其线性组合
4.1.1 n维向量的概念
显然的
向量组与矩阵的关系:

4.1.2 线性组合和线性表示
定义:
(一)线性组合:

(二)线性表示:

判定:转化为判定方程组有解问题,从而转化为求解矩阵的秩的问题 5
判定向量
b b A A 
判定向量组
B B A A 
该判定定理有以下推论:

判定向量组
B B A A 
4.2 向量组的线性相关性
定义:


判定:
定理一:

证明:按照定义,只需要移项 or 同除,进行构造即可
定理二:

证明:按照定义,转化为齐次线性方程组解的问题
- 有非零解
⇔ \Leftrightarrow R ( A ) = R ( A , 0 ) < m R(A)=R(A,0)<m - 仅有零解
⇔ \Leftrightarrow R ( A ) = R ( A , 0 ) = m R(A)=R(A,0)=m
- 有非零解
结论:
结论一:
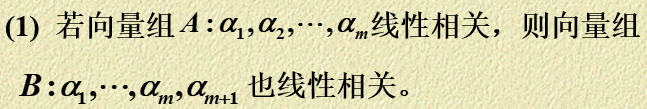
证明:
R ( A ) < m → R ( B ) ≤ R ( A ) + 1 < m + 1 R(A)<m \to R(B)\le R(A)+1 <m+1 结论二:

证明:
R ( A x × m ) = m → R ( A b ) = m R(A_{x\times m})=m \to R\binom{A}{b}=m 结论三:

证明:
R ( A ) ≤ n < m R(A)\le n <m 结论四:

证明:
R ( A ) = m , R ( A , b ) < m + 1 → A x = b 有唯一解 R(A)=m,R(A,b)<m+1 \to Ax=b\text{有唯一解} max { R ( A ) , R ( b ) } ≤ R ( A , b ) ≤ m + 1 → m ≤ R ( A , b ) ≤ m + 1 \max \{ R(A),R(b) \} \le R(A,b) \le m+1 \to m \le R(A,b) \le m+1 - 又
R ( A , b ) < m + 1 R(A,b)<m+1 - 故
R ( A , b ) = m R(A,b)=m - 因此
R ( A ) = R ( A , b ) = m → 有唯一解 R(A)=R(A,b)=m \to \text{有唯一解}
4.3 向量组的秩
4.3.1 最大无关组的定义
定义一:

注意:
- 最大无关组之间等价
- 最大无关组
A 0 A_0 A A
定义二:

4.3.2 向量组的秩和矩阵的秩的关系

4.3.3 向量组的秩的结论


证明:全部可以使用矩阵的秩的性质进行证明
4.4 向量空间
4.4.1 向量空间的概念
可以从高中学到的平面向量以及空间向量入手进行理解,即平面向量就是一个二维向量空间,同理空间向量就是一个三维向量空间,那么次数就是拓展到 n 维向量空间,道理是一样的,只不过超过三维之后就没有直观的效果展示罢了。
4.4.2 向量空间的基与维数
同样可以从高中学到的向量入手,此处的基就是基底,维数就是有几个基底。所有的基之间都是线性无关的,这是显然的。然后整个向量空间中任意一个向量都可以被基线性表示,也就很显然了,此处有三个考点,分别为:
考点一:求解空间中的某向量 x 在基 A 下的坐标
其实就是求解向量 x 在基 A 的各个“轴”上的投影。我们定义列向量
考点二:求解过度矩阵 P
我们已知一个向量空间中的两个基分别为 A 和 B,若有矩阵 P 满足基变换公式:
考点三:已知空间中的某向量 x 在基 A 下坐标为

4.5 线性方程组的解的结构
本目其实就是 3.3 目的一个知识补充,具体的线性方程组求解方法与 3.3 目几乎完全一致,只不过通过解的结构将解的结构进行了划分从而看似有些不同。但是殊途同归,都是一个东西。下面介绍本目与 3.3 目不同的地方:
我们从 3.3 目可以知道,无论是齐次线性方程组还是非齐次线性方程组,求解步骤都是:将系数矩阵(非齐次就是增广矩阵)进行行等价变换,然后对得到的方程组进行相对应未知变量的赋值即可。区别在于:
解释:我们将
- 齐次线性方程组记为
A x = 0 Ax=0 η \eta A η = 0 A \eta = 0 - 非齐次线性方程组记为
A x = b Ax=b η ∗ \eta^* A η ∗ = b A\eta^*=b η \eta A η = 0 A\eta=0 A ( η ∗ + η ) = b A(\eta^*+\eta)=b η ∗ + η \eta^* + \eta
也就是说本目对 3.3 目的线性方程组的求解给出了进一步的结构上的解释,即非齐次线性方程组的解的结构是基于本身的一个特解与齐次的通解之上的,仅此而已。当然了,本目在介绍齐次线性方程组解的结构时还引入了一个新的定理:
该定理可以作为一些证明秩相等的证明题的切入点。若想要证明两个$ n$ 元矩阵
第5章 相似矩阵及二次型
5.1 向量的内积、长度及正交性
5.1.1 内积
即各个位置的数依次相乘。运算规律如下:

推导全部按照内积的定义来,肥肠煎蛋
5.1.2 长度
类似于模长,有以下性质:

n 维向量与 n 维向量间的夹角:
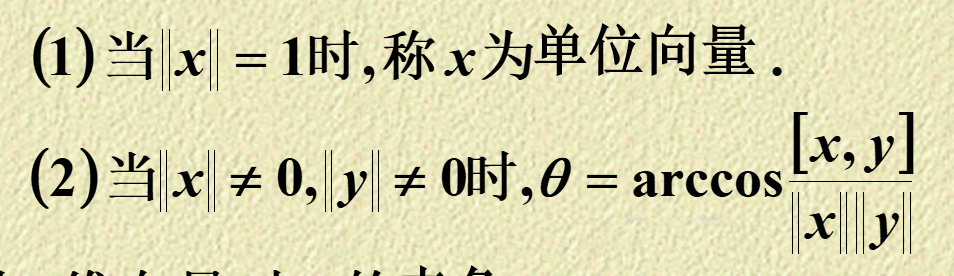
5.1.3 正交
类似于两个非零向量垂直的关系,即两向量内积为 0。
(一)正交向量组
- 定义:向量组之间的任意两两向量均正交
- 性质:正交向量组一定线性无关
(二)标准正交基
定义:是某空间向量的基+正交向量组+每一个向量都是单位向量
求解方法:施密特正交化
正交化:(其实就是对基础解系的一个线性组合)
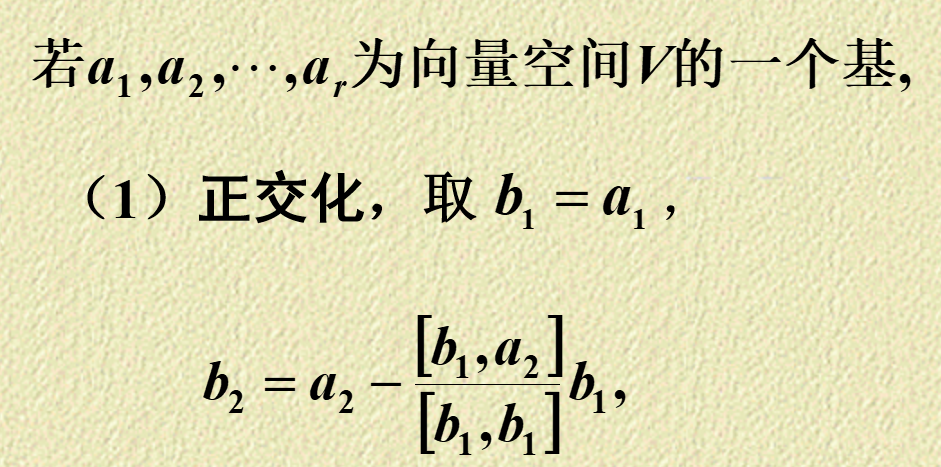
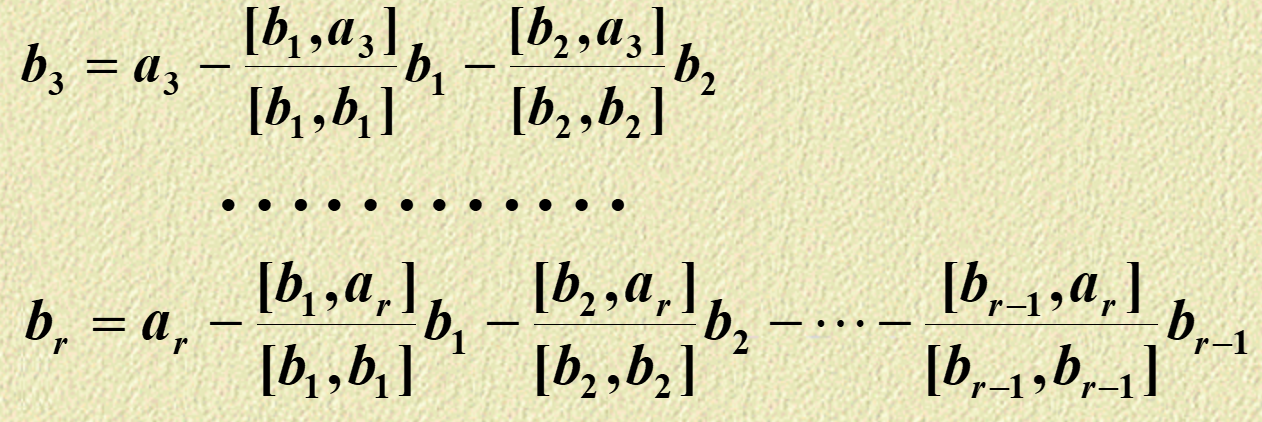
单位化:
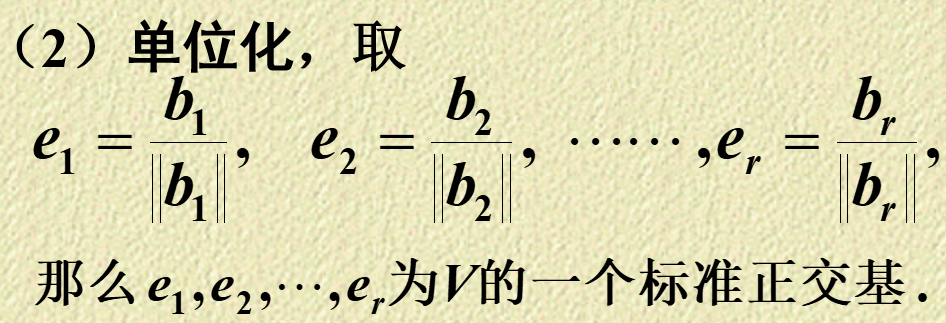
5.1.4 正交矩阵与正交变换
正交矩阵:(方阵)
- 定义:满足
A T A = E or A A T = E A^TA=E\ \text{or} \ AA^T=E - 定理:正交矩阵的充要条件为矩阵的行(列)向量为单位向量且两两正交
正交变换:
- 定义:对于正交矩阵
A A y = A x y=Ax - 性质:
∣ ∣ y ∣ ∣ = y T y = x T A T A x = x T E x = x T x = ∣ ∣ x ∣ ∣ ||y||=\sqrt{y^Ty}=\sqrt{x^TA^TAx}=\sqrt{x^TEx}=\sqrt{x^Tx}=||x||
5.2 方阵的特征值与特征向量
5.2.1 定义
对于一个n阶方阵 A,存在一个复数
则称 x 为特征向量,
5.2.2 特征值的性质
性质一
n阶矩阵 A 在复数范围内含有 n 个特征值,且
性质二
若
5.2.3 特征向量的性质
对于同一个矩阵,不同的特征值对应的特征向量之间是线性无关的
5.3 相似矩阵
5.3.1 定义
对于两个 n 阶方阵 A, B 而言,若存在可逆矩阵 P 使得
则称 B 为 A 的相似矩阵,A 与 B 相似,也称对 A 进行相似变换,P 为相似变换矩阵
5.3.2 性质
若矩阵 A 与 B 相似,则 A 与 B 的特征多项式相同,则 A 与 B 的特征值也就相同,A 与 B 的行列式也就相同
5.3.3 矩阵多项式
一个矩阵 A 的多项式
5.4 对称矩阵的对角化
本目讨论一个 n 阶方阵具备什么条件才能拥有 n 个线性无关的特征向量,从而可对角化。但是对于一般的方阵,情况过于复杂,此处只讨论 n 阶对称矩阵。即:一个 n 阶对角矩阵具备什么条件才能拥有 n 个线性无关的特征向量,从而可对角化。
答案是 n 阶对角矩阵一定是可对角化的。因为有一个定理是这样的:对于一个对称矩阵 A 而言,一定可以找到一个正交矩阵 P 使得
对称矩阵的性质
- 对称矩阵的特征值均为实数
- 对称矩阵 A 的两个特征值
λ 1 \lambda _1 λ 2 \lambda _2 P 1 P_1 P 2 P_2 λ 1 ≠ λ 2 \lambda_1 \ne \lambda_2 P 1 P_1 P 2 P_2 P 1 P_1 P 2 P_2 - 对称矩阵的每一个 k 重根,一定对应有 k 个线性无关的特征向量
因此本目相较于 5.3 目其实就是通过可对角化这一个概念,来告诉我们对称矩阵是一定可以求出对角矩阵的。而不用判断当前矩阵是否可对角化了。只不过在此基础之上还附加了一个小定理(也没给出证明),就是对称矩阵的相似变换矩阵一定是一个正交矩阵,那么也就复习回顾了 5.1 目中学到的正交矩阵的概念。为了求解出这个正交矩阵,我们需要在 5.3 目求解特征向量之后再加一个操作,即:对于一个 k 重根,根据上面的性质3我们知道当前的根一定有 k 个线性无关的特征向量,为了凑出最终的正交矩阵,我们需要对这 k 个线性无关的特征向量正交化。那么所有的特征值下的特征向量都正交化之后,又由性质2可知,不同的特征值下的特征向量又是正交的,于是最终的正交的相似变换矩阵也就求出来了,也就得到了对角矩阵
5.5 二次型及其标准型(部分)
本目只需要掌握到:将一个二次型转化为标准型,即可。其实就是比 5.4 目多一个将二次齐次函数的系数取出组成一个二次型的步骤。其中二次型就是一个对称矩阵。接着就是重复 5.4 目中的将对称矩阵转化为对角矩阵的过程了。
补
对称矩阵和正定性之间的关系
在最优化方法中我们需要通过目标函数海塞矩阵的正定性来判断凸性,显然的海塞矩阵是对称方阵。可以分别从特征值和行列式的角度进行判断。
特征值角度
- 一个对称矩阵 A 是正定的,当且仅当它的所有特征值
λ i > 0 \lambda_i>0 - 一个对称矩阵 A 是正半定的,当且仅当它的所有特征值
λ i ≥ 0 \lambda_i \ge 0
行列式角度
- 一个对称矩阵 A 是正定的,当且仅当所有主子矩阵的行列式都大于零
- 一个对称矩阵 A 是正半定的,当且仅当所有主子矩阵的行列式都大于或等于零
效果演示


[!note]
以下为课设报告内容
一、必做题
题目:编程实现希尔、快速、堆排序、归并排序算法。要求随机产生 10000 个数据存入磁盘文件,然后读入数据文件,分别采用不同的排序方法进行排序,并将结果存入文件中。
1.1 数据结构设计与算法思想
本程序涉及到四种排序算法,其中:
- 希尔排序:通过倍增方法逐渐扩大选择插入数据量的规模,而达到减小数据比较的次数,时间复杂度优化到近似
O ( n 1.65 ) O(n^{1.65}) - 快速排序:通过分治的算法策略,不断确定每一个数的最终位置,从而达到近似
O ( n log n ) O(n \log n) - 堆排序:通过堆的树形结构,减小两数的比较次数,最终通过不断维护堆结构来获得有序序列,时间复杂度为
O ( n log n ) O(n \log n) - 归并排序:通过分治排序回溯时左右两支有序的特点,进行归并,使算法整体的时间复杂度为固定的
O ( n log n ) O(n \log n)
1.2 程序结构
为了更好的了解排序算法内部的机制,我统计了每一种排序算法内部的比较次数,并结合了 Qt 的可视化框架进行编写。将四种排序作为算法内核嵌入 GUI 界面,程序结构如下:

UI
1 | |
Qt Application
1 | |
Algorithm
1 | |
1.3 实验数据与测试结果分析
原始数据序列生成算法使用时间种子的除留余数法,在数据规模为
| shell | heap | quick | merge | |
|---|---|---|---|---|
| 1 | 129419 | 231824 | 39061 | 120488 |
| 2 | 128051 | 232204 | 38723 | 120487 |
| 3 | 134873 | 231945 | 39052 | 120251 |
| 4 | 135719 | 232096 | 39158 | 120510 |
| 5 | 128821 | 232051 | 38747 | 120434 |
| average | 131376 | 232024 | 38948 | 120434 |
可以发现:在数据规模在
1.4 程序清单
/Src/Algorithm/sortAlgorithm.cpp:内核排序算法/Src/Forms/SortWidget.ui:ui 界面/Src/Headers/SortWidget.h:排序组件逻辑头文件/Src/Post/SortWidget.cpp:排序组件逻辑源文件/Src/Test/TestSort.cpp:程序测试文件
其中,除了 ui 界面使用 Qt Designer 设计师工具进行编写,其余文件均为与文件名同名的 C++ 类,便于维护与扩展
二、选做题
题三:扫描一个 C 源程序,利用两种方法统计该源程序中的关键字出现的频度,并比较各自查找的比较次数。
用 Hash 表存储源程序中出现的关键字,利用 Hash 查找技术统计该程序中的关键字出现的频度。用线性探测法解决 Hash 冲突。设 Hash 函数为 Hash(key) = [(key 的第一个字母序号) × 100 + (key 的最后一个字母序号)] % 41
用顺序表存储源程序中出现的关键字,利用二分查找技术统计该程序中的关键字出现的频度。
2.1 数据结构设计与算法思想
- 第一问:
首先用关键字序列构造哈希表,哈希函数使用题中所给,容易算出哈希表的最大容量为
25 × 100 + 40 25 \times 100+40 3000 3000 int: <string, int>的键值对形式,可以使用动态数组容器std::vector<std::pair>进行存储。其中键设为int可以使得对于一个int类型的哈希值进行O ( 1 ) O(1) <word, cnt>,即<std::string, int>然后对于文件中的每一个单词采用哈希搜索。利用哈希函数计算出每一个单词的哈希值,然后通过线性探测法进行搜索比对。关键在于如何解析出一个完整的单词,对于流读入的字符串(不包含空格、换行符、制表符等空白符),我们删除其中的符号后将剩余部分进行合并,之后进行异常处理,排除空串后进行哈希查找。查找次数包含成功和失败的比较次数
- 第二问:将关键字存储于顺序表中,排序后,利用二分查找技术进行搜索统计。查找次数包含成功和失败的比较次数
2.2 程序结构

UI
1 | |
Qt Application
1 | |
Algorithm
1 | |
2.3 实验数据与测试结果分析
代码文件从 github 上下载而来,其中 100 行与 500 行的代码文件为完整程序,2500 行代码文件为手动构造程序,三种文件数据规模的查找比较次数如下:
| self hash | binary hash | |
|---|---|---|
| 100 lines | 120 | 775 |
| 500 lines | 1546 | 10300 |
| 2500 lines | 5561 | 39097 |
可以发现:使用线性探测法进行哈希的比较次数远小于二分搜索的比较次数
2.4 程序清单
/Src/Algorithm/hashAlgorithm.cpp:内核哈希算法/Src/Forms/HashWidget.ui:ui 界面/Src/Headers/HashWidget.h:哈希组件逻辑头文件/Src/Post/HashWidget.cpp:哈希组件逻辑源文件/Src/Test/TestHash.cpp:程序测试文件
其中,除了 ui 界面使用 Qt Designer 设计师工具进行编写,其余文件均为与文件名同名的 C++ 类,便于维护与扩展
三、收获与体会
算法思维。四种排序算法总共也就 100 行,加上堆排序采用树形迭代,快排与归并排序采用递归,整体编码难度并不算高。即使加上了文件 I/O 操作也不过 150 行。而第二道题也是 hash 查找与 binary 查找加上文件 I/O 操作,整体算法难度也十分有限。但是对于我来说也加强了 hash 构建与查找的逻辑。
前后端开发。为了锻炼设计模式思维与软件工程思维,我加入了 Qt 集成的 GUI 界面,不仅体会到了算法对于软件的核心作用所在,也体会到了窗口程序的数据交互与数据接口的开发过程。比如 Qt 中信号与槽的概念,其实就是一种数据交互的 API 格式。同时在体验开发过程的同时,也感受到了用户体验的前端板块,通过使用 Qt Designer 的设计师开发界面,可以通过拖动组件的形式进行可视化设计界面,提高了开发效率,如果可以多人组队,也实现了前后端分离的同步开发模式。
异常处理。与传统 OJ 不同的是,一个软件还需要考虑更多的异常处理,没有标准的 std 数据,加上用户输入、操作的无穷性,注定了软件的异常处理不是一个简单的事,比如在解析用户输入的字符串以及解析用户按钮操作的过程中,需要添加很多的字符串处理结构以及事件触发处理结构,这对于我强化软件开发的健壮性很有帮助。
版本管理。通过 Git 版本管理与 Github 的云端同步功能,也更能体会到开发留痕与 bug 检测的优势。
当然美中不足的也有很多,比如单人全栈开发并不利于锻炼团队协作的能力,同时对于程序的架构设计也没有经过深度考虑,仅仅有界面,数据正常交互就戛然而止。希望在未来的算法与开发路上可以走的更远、更坚定。
仓库地址
github: https://github.com/Explorer-Dong/DataStructureClassDesign
gitee: https://gitee.com/explorer-dong/DataStructureClassDesign
]]>问题介绍
在 Clion 的默认设置下,输出中文会出现乱码,如下
1 | |
输出
1 | |
解决方案
编码问题就需要修改编码方式,按照下面的流程进行操作即可
进入设置
选择 Editor 中的 File Encodings
将这两个下拉框中的选项全部选择为 UTF-8,点击 OK
在主页面的右下角,将这个选项设置为 GBK
选择 Convert
重新运行即可😎
1 | |
前言
为了在比赛中不因为编辑器而拖后腿,写一个配置说明。编辑器为 Dev-C++ 5.11
一、编译标准
进入以下目录:
添加以下编译命令:
二、环境选项

三、编辑器选项
进入以下目录:

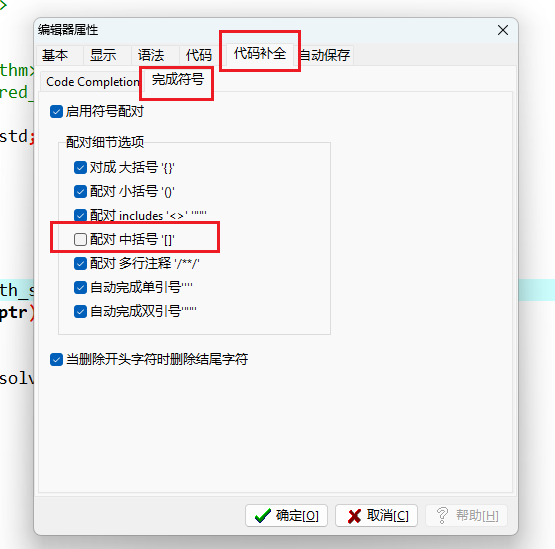
四、快捷键选项
进入以下目录:
设置注释配置:

前言
为了在比赛中不因为编辑器而拖后腿,写一个配置说明。编辑器为 Dev-C++ 5.11
一、编译标准
进入以下目录:

添加以下编译命令:

二、环境选项


三、编辑器选项
进入以下目录:


四、快捷键选项
进入以下目录:

设置注释配置:

问题介绍
在 Clion 的默认设置下,输出中文会出现乱码,如下
1 | |
输出
1 | |
解决方案
编码问题就需要修改编码方式,按照下面的流程进行操作即可
进入设置
选择 Editor 中的 File Encodings
将这两个下拉框中的选项全部选择为 UTF-8,点击 OK
在主页面的右下角,将这个选项设置为 GBK
选择 Convert
重新运行即可😎
1 | |
【二维/数学】Minimum Manhattan Distance
https://codeforces.com/gym/104639/problem/J
题意:给定两个圆的直径的两个点坐标,其中约束条件是两个圆一定是处在相离的两个角上。问如何在C2圆上或圆内找到一点p,使得点p到C1圆的所有点的曼哈顿距离的期望值最小
思路:
看似需要积分,其实我们可以发现,对于点p到C1中某个点q1的曼哈顿距离,我们一定可以找到q1关于C1对称的点q2,那么点p到q1和q2的曼哈顿距离之和就是点p到C1的曼哈顿距离的两倍(证明就是中线定理)那么期望的最小值就是点p到C1的曼哈顿距离的最小值。目标转化后,我们开始思考如何计算此目标的最小值,思路如下图
注意点:
- double的读取速度很慢,可以用
intorlong long读入,后续强制类型转换(显示 or 和浮点数计算)- 注意输出答案的精度控制
cout << fixed << setprecision(10) << res << "\n";
1 | |
【枚举】三角形
https://www.acwing.com/problem/content/5383/
题意:给定两个直角三角形的两条直角边的长度 a, b,问能不能在坐标轴上找到三个整数点使得三点满足该直角三角形且三遍均不与坐标轴垂直
思路:首先确定两个直角边的顶点为原点 (0, 0),接着根据对称性直接在第一象限中按照边长枚举其中一个顶点 A,对于每一个枚举到的顶点 A,按照斜率枚举最后一个顶点 B,如果满足长度以及不平行于坐标轴的条件就是合法的点。如果全部枚举完都没有找到就是没有合法组合,直接输出 NO 即可。
时间复杂度:
O ( a 2 b ) O(a^2b)
1 | |
【凸包】奶牛过马路
https://www.acwing.com/problem/content/5572/
题意:给定一个二维坐标系,现在有两个东西可以进行平移。
- 一个是起始位于
的奶牛,可以沿着 ( 0 , 0 ) (0,0) 轴以 y y 的速度正向或负向移动 [ 0 , u ] [0,u] - 一个是起始位于第一象限的凸包形状的车辆,可以向
轴负半轴以恒定的速度 x x 移动 v v 在给定凸包的
个顶点的情况下,以及不允许奶牛被车辆撞到的情况下,奶牛前进到 n n 的最短时间 ( 0 , w ) (0,w) 思路:由于是凸包,因此每一个顶点同时满足的性质,就可以代表整个凸包满足的性质。那么对于奶牛和凸包,就一共有三个局面:
- 奶牛速度足够快。可以使得对于任意一个顶点
在到达 y 轴时,都小于此时奶牛的 y 值,用时间来表示就是 ( x , y ) (x,y) ,即 y u ≤ x v \frac{y}{u} \le \frac{x}{v} ,表示凸包上所有的顶点都在直线 y ≤ u v x y \le \frac{u}{v}x 的下方 y = u v y=\frac{u}{v} - 凸包速度足够快。可以使得对于任意一个顶点
在到达 y 轴时,都大于此时奶牛的 y 值,用时间来表示就是 ( x , y ) (x,y) ,即 y u ≥ x v \frac{y}{u} \ge \frac{x}{v} ,表示凸包上所有的顶点都在直线 y ≥ u v x y \ge \frac{u}{v}x 的上方 y = u v y=\frac{u}{v} - 上述两种都不满足,即直线
与凸包相交。此时奶牛就不能一直全速(u)前进到终点了,需要进行一定的减速 or 返回操作。有一个显然的结论就是,对于减速 or 返回的操作,都可以等价于后退一段距离后再全速(u)前进,因此对于需要减速 or 返回的操作,我们只需要计算出当前状态下应该后退的距离即可。再简洁的,我们就是需要平移直线 y = u v y=\frac{u}{v} ,显然只能向下平移而非向上平移,因此其实就是计算出直线 y = u v y=\frac{u}{v} 的截距 y = u v + b y=\frac{u}{v}+b 使得最终的直线 b b 满足第二种条件即可。那么如何计算这个 b 呢?很显然我们可以遍历每一个顶点取满足所有顶点都在直线 y = u v + b y=\frac{u}{v}+b 上方的最大截距 b 即可。 y = u v + b y=\frac{u}{v}+b 注意点:
- 浮点数比较注意精度误差,尽可能将除法转化为乘法
- 在比较相等时可以引入一个无穷小量
ϵ = 1 0 − 7 \epsilon=10^{-7} - 注意答案输出精度要求,
就需要我们出至少 1 0 − 6 10^{-6} 位小数 7 7 时间复杂度:
O ( n ) O(n)
C++
1 | |
Py
1 | |
思考如何必胜态和必败态是什么以及如何构造这样的局面。
【博弈/贪心/交互】Salyg1n and the MEX Game
https://codeforces.com/contest/1867/problem/C
标签:博弈、贪心、交互
题面:对于给定n个数的数列,先手可以放入一个数列中不存在的数(0-1e9),后手可以从数列中拿掉一个数,但是这个数必须严格小于刚才先手放入的数。终止条件:后手没法拿数或者操作次数达到了 2n+1 次。问:当你是先手时,如何放数可以使得最终数列的 MEX 值最大。
思路:先手每次放入的数一定是当前数列的 MEX 值,此后不管后手拿掉什么数,先手都将刚刚被拿掉的数放进去即可。那么最多操作次数就刚好是 2n+1次,因为加入当前数列就是一个从 0 开始的连续整数数列,那么先手放入的数就是最大数 +1,即 n,那么假如后手从 n-1 开始拿,后手最多拿 n 次,先手再放 n 次,那么就是 2n+1 次。
时间复杂度:
O ( n ) O(n)
1 | |
思考如何必胜态和必败态是什么以及如何构造这样的局面。
【博弈/贪心/交互】Salyg1n and the MEX Game
https://codeforces.com/contest/1867/problem/C
标签:博弈、贪心、交互
题面:对于给定n个数的数列,先手可以放入一个数列中不存在的数(0-1e9),后手可以从数列中拿掉一个数,但是这个数必须严格小于刚才先手放入的数。终止条件:后手没法拿数或者操作次数达到了 2n+1 次。问:当你是先手时,如何放数可以使得最终数列的 MEX 值最大。
思路:先手每次放入的数一定是当前数列的 MEX 值,此后不管后手拿掉什么数,先手都将刚刚被拿掉的数放进去即可。那么最多操作次数就刚好是 2n+1次,因为加入当前数列就是一个从 0 开始的连续整数数列,那么先手放入的数就是最大数 +1,即 n,那么假如后手从 n-1 开始拿,后手最多拿 n 次,先手再放 n 次,那么就是 2n+1 次。
时间复杂度:
O ( n ) O(n)
1 | |
【拓扑】有向图的拓扑序列
https://www.acwing.com/problem/content/850/
题意:输出一个图的拓扑序,不存在则输出-1
思路:
- 首先我们要知道拓扑图的概念,感官上就是一张图可以从一个方向拓展到全图,用数学语言就是:若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列
- 接着我们就想要寻找这样的序列 A 了,可以发现对于每一个可扩展的点,入度一定为0,那么我们就从这些点开始宽搜,将搜到的点的入度-1,即删除这条边,直到最后。如果全图的点的入度都变为了0,则此图可拓扑
时间复杂度:
O ( n + m ) O(n+m)
1 | |
【基环树/拓扑】Mad City🔥
https://codeforces.com/contest/1873/problem/H
tag:基环树、拓扑排序
题意:给定一个基环树,现在图上有两个点,分别叫做A,B。现在B想要逃脱A的抓捕,问对于给定的局面,B能否永远逃离A的抓捕
思路:思路很简单,我们只需要分B所在位置的两种情况讨论即可
- B不在环上:此时我们记距离B最近的环上的那个点叫
,我们需要比较的是A到tag点的距离 t a g tag 和B到tag的距离 d A d_A ,如果 d B d_B ,则一定可以逃脱,否则一定不可以逃脱 d B < d A d_B < d_A - B在环上:此时我们只需要判断当前的A点是否与B的位置重合即可,如果重合那就无法逃脱,反之B一定可以逃脱。
代码实现:
- 对于第一种情况,我们需要找到tag点以及计算A和B到tag点的距离,
时间复杂度:
1 | |
【二分图】染色法判定二分图
https://www.acwing.com/problem/content/862/
题意:给定一个无向图,可能有重边和自环。问是否可以构成二分图。
二分图的定义:一个图可以被分成两个点集,每个点集内部没有边相连(可以不是连通图)
思路:利用染色法,遍历每一个连通分量,选择连通分量中的任意一点进行染色扩展
- 如果扩展到的点没有染过色,则染成与当前点相对的颜色
- 如果扩展到的点已经被染过色了且染的颜色和当前点的颜色相同,则无法构成二分图(奇数环)
时间复杂度:
O ( n + e ) O(n+e)
1 | |
【最小生成树】Kruskal算法求最小生成树
https://www.acwing.com/problem/content/861/
题意:给定一个无向图,可能含有重边和自环。试判断能否求解其中的最小生成树,如果可以给出最小生成树的权值
思路:根据数据量,可以发现顶点数很大,不适用
算法,只能用 P r i m Prim 算法,下面简单介绍一下该算法的流程 K r u s k a l Kruskal
- 自环首先排除 - 显然这条边连接的“两个”顶点是不可能选进
的 M S T MST - 首先将每一个结点看成一个连通分量
- 接着按照权值将所有的边升序排序后,依次选择
- 如果选出的这条边的两个顶点不在一个连通分量中,则选择这条边并将两个顶点所在的连通分量合并
- 如果选出的这条边的两个顶点在同一个连通分量中,则不能选择这条边(否则会使得构造的树形成环)
- 最后统计选择的边的数量
进行判断即可 n u m num
,则可以生成最小生成树 n u m = n − 1 num=n-1 ,则无法生成最小生成树 n u m < n − 1 num<n-1 - 时间复杂度:
- 因为最大的时间开销在对所有的边的权值进行排序上 O ( e log e ) O(e\log e)
C++
1 | |
Python
1 | |
JavaScript
1 | |
【最小生成树】Prim算法求最小生成树
https://www.acwing.com/problem/content/860/
题意:给定一个稠密无向图,有重边和自环。求出最小生成树
思路:根据题目的数据量,可以使用邻接矩阵存储的方法配合
算法求解最小生成树,下面给出该算法的流程 P r i m Prim
- 首先明确一下变量的定义:
g[i][j]为无向图的邻接矩阵存储结构MST[i]表示号点是否加入了 i i 集合 M S T MST d[i]表示i号点到集合的最短边长度 M S T MST - 自环不存储,重边只保留最短的一条
- 任选一个点到集合
中,并且更新 M S T MST 数组 d d - 选择剩余的
个点,每次选择有以下流程 n − 1 n-1
- 找到最短边,记录最短边长度
和相应的在 e e 集合中对应的顶点序号 U − M S T U-MST v v - 将
号点加入 v v 集合,同时根据此时选出的最短边的长度来判断是否存在最小生成树 M S T MST - 根据
号点,更新 v v 数组,即更新在集合 d d 中的点到 U − M S T U-MST 集合中的点的交叉边的最短长度 M S T MST - 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【最短路】Dijkstra求最短路 🔥
朴素版 - https://www.acwing.com/problem/content/851/
堆优化 - https://www.acwing.com/problem/content/852/
题意:给定一个正边权的有向图,可能存在重边与自环,问
号点到 1 1 号点的最短路径长度是多少,如果不可达就输出 n n 。 − 1 -1 思路一:朴素版。点数
,边数 1 ≤ n ≤ 500 1\le n \le 500 1 ≤ m ≤ 1 0 5 1 \le m\le 10^5
思路:根据数据量,我们采用邻接矩阵的方式存储「点少边多」的稠密图。我们定义
d[i]数组表示起点到i号点的最短距离。先将起点放入SPT (Shortest Path Tree)集合,然后更新所有V-SPT中的点到SPT集合的最短路径长度。接着循环n-1次迭代更新剩余的n-1个点,每次迭代的过程中,首先选择距离起点最近的点vex,然后将该点加入SPT集合,最后利用该点更新V-SPT集合中和该点有连边的点到起点的最短距离。最终的d[end]就是起点start到终点end的最短距离。总结:算法整体采用贪心与动态规划的思路。与
算法仔细比对可知,其中的贪心过程几乎一致,即每次选择加入 SPT 集合的点均为当前局面 Prim \text{Prim} V-SPT集合中距离起点最近的点。而动态规划的过程体现在,在求解出集合V-SPT中到集合STP最短距离的点vex之后,利用该点对「在V-SPT集合且和 vex 点有连边的点i」更新d[i]的过程。更新前的状态都是在之前的子结构下的最优解。时间复杂度:
O ( n 2 ) O(n^2) 思路二:堆优化。点数
,边数 1 ≤ n ≤ 1.5 × 1 0 5 1\le n \le 1.5 \times 10^5 1 ≤ m ≤ 1.5 × 1 0 5 1 \le m \le 1.5 \times 10^5
思路:根据数据量,我们采用邻接表的方式存储「点多边少」的稀疏图。如果采用上述朴素 Dijkstra 算法进行求解必然会因为点数过多而超时,因此我们利用数据结构「堆」进行时间开销上的优化。不难发现朴素 Dijkstra 算法在迭代过程中主要有三部分:
- 选择距离起点最近的点
vex。因为需要枚举所有的顶点,因此总的时间复杂度为O ( n 2 ) O(n^2) - 将该点加入
SPT集合。因为只是简单的打个标记,因此总的时间复杂度为O ( n ) O(n) - 利用该点更新
V-SPT集合中和该点相连的点到起点的最短距离。因为此时枚举的是该点所有的连边,而邻接表的图存储方式无法进行重边的删除,因此最坏情况下会枚举所有的边,时间复杂度为O ( m ) O(m) 时间复杂度:
朴素版C++:
1 | |
朴素版Python:
1 | |
堆优化版C++:
1 | |
【最短路】Floyd求最短路
https://www.acwing.com/problem/content/856/
题意:给定一个稠密有向图,可能存在重边与自环,给出多个询问,需要给出每一个询问的两个点之前的最短路径长度
思路:我们采用动态规划的思路。在此使用多阶段决策的方法,即每一个路径状态为选择
个点的情况下的最短路径长度 1 → k 1\to k
- 状态表示:
f[k][i][j]表示在前个顶点中进行选择(中转), k k 号点到 i i 号点的最短路径长度 j j - 状态转移:对于第
个顶点,我们可以选择中转,也可以不中转。 k k
- 对于不选择中转的情况:
f[k][i][j] = f[k-1][i][j]- 对于可选择中转的情况:
f[k][i][j] = f[k-1][i][k] + f[k-1][k][j]- 在其中取最小值即可,但是有一个注意点:对于第二种情况,选择是有一个约束的:即如果选择了
号点进行转移的话,那么 k k 号点到 i i 号点以及 k k 号点到 k k 号点都是需要有路径可达的,从而可以选择最小距离 j j - 初始化:即选择 0 个站点进行中转时,即
f[0][i][j]的情况中,
- 如果
号点与 i i 号点自环,则取 j j 0 0 - 如果
号点与 i i 号点之间有边,则取重边的最小值 j j - 如果
号点与 i i 号点之间无边,则初始化为正无穷 j j - 答案状态:对于
号点到 a a 号点之间的最小路径长度,就是 b b f[n][a][b]- 时间复杂度:
O ( n 3 ) O(n^3) - 空间复杂度:
O ( n 3 ) O(n^3) 空间优化推导:我们尝试优化掉记忆数组的第一维度
对于不选择的情况:由于决策局面
是从前往后枚举,故当前状态 k k f[k][i][j]可以直接依赖于已经更新出来且不会被当前状态之后的状态再次覆盖的最优子结构f[i][j]。即上一个局面的选择情况,就是不选择第个顶点的情况 k k 对于选择的情况:如果删除第一维度,我们担心的是当前状态
f[k][i][j]依赖的两个状态f[i][k]与f[k][j]会不会被后续覆盖掉,即我们不确定f[i][k]与f[k][j]是否是当前第 k 个局面的最优子结构。尝试推导:为了确定
f[i][k]与f[k][j]是否是当前第个局面的最优子结构,其实就是确定对于当前第 k k 个局面,这两个状态会不会在当前状态 k k f[i][j]之后被更新覆盖,那么我们就看这两个状态是从哪里转移过来进行更新的。如果f[i][k]与f[k][j]这两个状态的转移会依赖于当前状态之后的状态,那么删除第一维度就是错误的,反之就是成立的。尝试推导
f[i][k]与f[k][j]从何转移更新:利用我们未删除维度时正确的状态转移方程进行推演我们知道:
f[k][i][k] = min(f[k-1][i][k], f[k-1][i][k] + f[k-1][k][k]),其中的f[k-1][k][k]就是一个自环的路径长度,由于算法的约束条件是没有负环,因此 f l o y d floyd f[k-1][k][k]一定大于零,故f[k][i][k]一定取前者,即f[k][i][k] = f[k-1][i][k]同理可知:
f[k][k][j] = f[k-1][k][j]基于上述推导我们可以知道,当前第
个决策局面中的 k k f[k][i][k]与f[k][k][j]是依赖于上一个决策局面的,也就是说这两个状态一定是早于当前状态 k − 1 k-1 f[i][j]被更新覆盖的,故f[i][k]与f[k][j]就是当前第个局面的最优子结构,证毕,可以进行维度的删除 k k 时间复杂度:
O ( n 3 ) O(n^3) 空间复杂度:
O ( n 2 ) O(n^2)
不优化空间
1 | |
优化空间
1 | |
【最短路】关闭分部的可行集合数目
https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/
标签:二进制枚举、最短路
题意:给定一个含有
个顶点的无向图,如何删点可以使得剩余的图中顶点两两可达且最大距离不超过 maxDistance?返回所有删点的方案数。 n n 思路:由于
的数据范围只有 n n ,我们可以直接枚举所有的删点方案。那么如何检查一个方案的合法性呢?直接使用最短路算法检查「所有顶点到每一个顶点」的最远距离即可。这里我们采用朴素 dijkstra 算法。 1 → 10 1 \to 10 时间复杂度:
- 其中枚举需要 O ( 2 n × n 3 ) O(2^n \times n^3) 、计算所有顶点到某个顶点的最远距离需要 O ( 2 n ) O(2^n) 、检查所有顶点需要 O ( n 2 ) O(n^2) O ( n ) O(n)
1 | |
1 | |
【思维/遍历】图的遍历
https://www.luogu.com.cn/problem/P3916
题意:给定一个有向图,求解每一个点可以到达的编号最大的点
思路:如果从正向考虑,很显然的一个暴力方法就是对于每一个点都跑一遍 dfs 或者 bfs 获取可达的最大点编号,时间复杂度
,如果想要在遍历的过程中同时更新其余的点,那只有起点到最大点之间的点可以被更新,可以通过递归时记录路径点进行,时间复杂度几乎不变。我们尝试反向考虑:反向建边。既然正向考虑时需要标记的点为最大点与起点的路径,那不如直接从最大值点开始遍历搜索,在将所有的边全部反向以后,从最大值点开始遍历图,这样就可以在线性时间复杂度内解决问题 O ( n 2 ) O(n^2) 时间复杂度:
O ( n + m ) O(n+m)
bfs 代码
1 | |
dfs 代码
1 | |
【遍历/并查集】孤立点数量
https://www.acwing.com/problem/content/5560/
题意:给定一个无向图,可能不连通,没有重边和自环。现在需要给图中的每一条无向边定向,要求所有的边定完向以后 0 入度的点尽可能的少,给出最少的 0 入度点的数量
思路:我们知道对于一棵树而言,n 个结点一共有 n-1 条边,也就可以贡献 n-1 个入度,因此至少有一个点的入度为 0。而如果不是一棵树,就会有至少 n 条边,也就至少可以贡献 n 个入度,那么 n 个结点就至少全都有入度了。显然的,一个图至少含有 n 条边时就一定有环。有了上述思路以后就可以发现,这道题本质上就是在判断连通分量是否含有环,如果有环,那么该连通分量定向边以后就不会产生 0 入度的顶点,反之,如果没有环,那么定向边以后最少产生 1 个 0 入度的点。
算法一:遍历图。我们采用 dfs 遍历的方式即可解决问题。一边遍历一边打标记,遇到已经打过标记的非父结点就表明当前连通分量有环。我们使用 C++ 实现
时间复杂度:
O ( n + m ) O(n+m) 算法二:并查集。由于没有重边,因此在判断每一个连通分量是否含有环时,可以直接通过该连通分量中点和边的数量关系得到结果。我们使用 Python 和 JavaScript 实现
时间复杂度:
O ( n ) O(n)
C++
1 | |
Python
1 | |
JavaScript
1 | |
【LCA】树的直径
https://www.acwing.com/problem/content/5563/
题意:给定一棵树,初始时含有 4 个结点分别为 1 到 4,其中 1 号为根结点,2 到 4 均为根结点的叶子结点。现在进行 Q 次操作,每次指定一个已经存在的结点向其插入两个新结点作为叶节点。现在需要在每次操作以后输出这棵树的直径。我们定义树的直径为:树中距离最远的两个点之间的距离。
思路一:暴力搜索。
我们将树重构为无向图,对于每一个状态的无向图,首先从任意一个已存在的结点 A 开始搜索到距离他最远的点 B,然后从 B 点出发搜索到离他最远的点 C,则 B 与 C 之间的距离就是当前状态的树的直径。由于每一个状态的树都要遍历两遍树,于是时间复杂度就是平方阶
时间复杂度:
O ( q n ) O(qn) 思路二:最近公共祖先 LCA。
从树的直径出发。我们知道,树的直径由直径的两个结点之间的距离决定,因此我们着眼于这两个结点
和 A A 展开。不妨设当前局面直径的两个结点已知为 B B 和 A A ,现在插入两个叶子结点 B B 和 L 1 L_1 。是否改变了树的直径大小取决于新插入的两个结点对于当前树的影响情况。如果 L 2 L_2 或 L 1 L_1 可以替代 L 2 L_2 或 A A ,则树的直径就会改变。很显然新插入的两个叶子结点对于直径的两个端点影响是同效果的,因此我们统称新插入的叶子结点为 B B 。 L L 什么时候树的直径会改变?对于
、 A A 和 B B 来说,直径是否改变取决于 L L 能否替代 L L 或 A A ,一共有六种情况。我们记 B B , dist ( A , L ) = d a \text{dist}(A,L)=da ,当前树的直径为 dist ( B , L ) = d b \text{dist}(B,L)=db ,六种情况如下: r e s res
,交换 max ( d a , d b ) ≤ res \text{max}(da, db) \le \text{res} 和 A A 得到 B B 种 2 2 ,交换 min ( d a , d b ) ≥ res \text{min}(da,db) \ge \text{res} 和 A A 得到 B B 种 2 2 ,交换 max ( d a , d b ) > r e s , min ( d a , d b ) < res \text{max}(da,db) >res,\text{min}(da,db) < \text{res} 和 A A 得到 B B 种 2 2 如图:我们只需要在其中的最大值严格超过当前树的直径
时更新直径对应的结点以及直径的长度即可 res \text{res}
如何快速计算树上任意两个点之间的距离?我们可以使用最近公共祖先 LCA 算法。则树上任意两点
之间的距离 x , y x,y 为: dist ( x , y ) \text{dist}(x,y)
dist ( x , y ) = dist ( x , r o o t ) + dist ( y , r o o t ) − 2 × dist ( lca ( x , y ) , r o o t ) \text{dist}(x,y) = \text{dist}(x,root) + \text{dist}(y,root) - 2 \times \text{dist}(\text{lca}(x,y),root) 时间复杂度:
O ( q log n ) O(q \log n)
暴力搜索代码
1 | |
LCA 代码
1 | |
【哈希】分组
https://www.acwing.com/problem/content/5182/
存储不想同组和想同组的人员信息:存入数组,数据类型为一对字符串
存储所有的组队信息:存入哈希表,数据类型为“键:字符串”“值:一对字符串”
想要知道最终的分组情况,只需要查询数组中的队员情况与想同组 or 不想同组的成员名字是否一致即可
时间复杂度
,空间复杂度 O ( n ) O(n) O ( n l e n ( n a m e ) ) m a x O(n\ len(name))_{max}
1 | |
【哈希】海港
https://www.luogu.com.cn/problem/P2058
- 题意:给定 n 艘船只的到达时间、载客信息(载客人数和每一个客人的国籍),现在需要知道对于每一艘抵达的船只,前 24 小时中抵达的客人的国籍总数
- 思路:本题思路很简单,就是一个队列的应用以及哈希客人国籍的过程。由于船只抵达的时间是顺序增加的,故每抵达一艘船只,就对新来的客人国籍进行哈希,为了计算前 24 小时的情况,需要对船只抵达队列进行删减,即只保留 24 小时以内的船只抵达信息。对于删除的船只信息,需要将这些船只上的客人国籍信息从哈希表中删除,故每一艘船只的访问次数为 2。
unordered_map补充:在进行哈希统计时。为了判断当前 24 小时内客人国籍数,在删除哈希记录时,为了判断是否将当前国籍的游客全部删除时,需要统计哈希表中某个国籍是否减为了 0,我用了.count(x)内置方法,但这是不正确的,因为我想要统计的是 值 是否为 0,而.count(x)统计的是哈希表中 x 这个 键 的个数,而unordered_map中是没有重复的键的,故.count(x)方法只会返回 0 或 1,返回 0 就表示当前哈希表中没有 x 这个键,返回 1 就表示哈希表中有 x 这个键,但是有这个键不代表对应的值就存在,可能是x: 0的情况,即键存在,但是值记录为 0- 时间复杂度:
- 即两倍的所有游客数 O ( 2 ∑ x i ) O(2 \sum x_i)
1 | |
【哈希】Cities and States S
https://www.luogu.com.cn/problem/P3405
题意:给定 n 个字符串,每一个字符串归属一个集合,现在需要统计字符串与集合名相反相等的对数
思路:很显然的哈希计数。难点有两个,如何哈希?如何计数?哈希可以采用扩展字符的方法进行,即第一个字符乘某一个较大的质数再加上第二个字符。此处采用一种较为巧妙的方法,直接将两个字符串与集合名加起来进行唯一性哈希,降低编码难度。计数有两种方式,第一种就是全部哈希结束之后,再遍历哈希表进行统计,最后将结果除二即可。第二种就是边哈希边计数,遇到相反相等的就直接计数,这样就不会重复计数了,也很巧妙
时间复杂度:
O ( n ) O(n)
1 | |
【哈希/枚举/思维】Torn Lucky Ticket
https://codeforces.com/contest/1895/problem/C
题意: 给定一个长度为 n 的字符串数组 nums, 数组的每一个元素长度不超过 5 且仅由数字组成. 问能找到多少对
可以使得拼接后的 ( i , j ) (i,j) 长度为偶数且左半部分的数字之和与右半部分的数字之和相等. n u m s [ i ] + n u m s [ j ] nums[i]+nums[j] 思路:
首先最暴力的做法就是
枚举,所有的 O ( n 2 ) O(n^2) 然后 check 合法性. ( i , j ) (i,j) 尝试优化掉第二层的枚举循环. 对于第二层循环, 我们就是要寻找合适的
并和当前的 n u m s [ j ] nums[j] 拼接. 显然我们可以通过扫描当前的 n u m s [ i ] nums[i] 并 n u m s [ i ] nums[i] 的计算出所有 O ( 1 ) O(1) 且可以和 l e n ( n u m s [ j ] ) ≤ l e n ( n u m s [ i ] ) len(nums[j])\le len(nums[i]) 匹配的字符串的 n u m s [ i ] nums[i] [长度][数字和]信息, 只需要一个二维数组预存储每一个字符串的 长度 数字和 信息即可.那么对于
的情况如何统计呢. 显然此时我们没法 l e n ( n u m s [ j ] ) > l e n ( n u m s [ i ] ) len(nums[j])> len(nums[i]) 的检查 O ( 1 ) O(1) 的合法性. 不妨换一个角度, 当我们枚举 n u m s [ i ] + n u m s [ j ] nums[i]+nums[j] 时: n u m s [ i ] nums[i]
统计右侧拼接长度更大的 nums[j] 的合法情况数 ⟺ 统计左侧拼接长度更小的 nums[j] 的合法情况数 \text{统计右侧拼接长度更大的 nums[j] 的合法情况数} \iff \text{统计左侧拼接长度更小的 nums[j] 的合法情况数} 于是合法情况数就可以表示为
, 其中第一种情况 ∑ i = 0 n − 1 [ cond 1 ( n u m s [ i ] ) + cond 2 ( n u m s [ i ] ) ] \displaystyle \sum_{i=0}^{n-1}\big[\text{cond}_1(nums[i])+\text{cond}_2(nums[i])\big] 就是统计右侧拼接长度更小的字符串数量, 第二种情况 cond 1 \text{cond}_1 就是统计左侧拼接长度更小的字符串数量. 这两步可以同时计算. cond 1 \text{cond}_1 时间复杂度:
O ( n ) O(n)
1 | |
大胆猜测,小心求证(不会证也没事,做下一题吧)。证明方法总结了以下几种
- 反证法:假设取一种方案比贪心方案更好,得出相反的结论
- 边界法:从边界开始考虑,因为满足边界条件更加容易枚举,从而进行后续的贪心
- 直觉法:遵循社会法则()
1. green_gold_dog, array and permutation
https://codeforces.com/contest/1867/problem/A
题意:给定n个数a[i],其中可能有重复数,请构造一个n个数的排列b[i],使得c[i]=a[i]-b[i]中,c[i]的不同数字的个数最多
思路:思路比较好想,就是最大的数匹配最小的数,次大的数匹配次小的数,以此类推。起初我想通过将原数列的拷贝数列降序排序后,创建一个哈希表来记录每一个数的排位,最终通过原数列的数作为键,通过哈希表直接输出排位,但是问题是原数列中的数可能会有重复的,那么在哈希的时候如果有重复的数,那么后来再次出现的数就会顶替掉原来的数的排位,故错误。
正确思路:为了保证原数列中每个数的唯一性,我们可以给原数列每一个数赋一个下标,排序后以下标进行唯一的一一对应的索引。那么就是:首先赋下标,接着以第一关键词进行排序,然后最大的数(其实是下标)匹配最小的结果以此类推
模拟一个样例:
5
8 7 4 5 5 9最终的答案应该是
2 3 6 4 5 1首先对每一个数赋予一个下标作为为唯一性索引
8 7 4 5 5 9
1 2 3 4 5 6(替身)接着将上述数列按照第一关键词进行排序
9 8 7 5 5 4
6 1 2 4 5 3(替身)对每一个数进行赋值匹配
9 8 7 5 5 4
6 1 2 4 5 3(替身)
1 2 3 4 5 6(想要输出的结果)按照替身进行排序
8 7 4 5 5 9
1 2 3 4 5 6(替身)(排序后)
2 3 6 4 5 1(想要输出的结果)
1 | |
2. Good Kid
https://codeforces.com/contest/1873/problem/B
题意:对于一个数列,现在可以选择其中的一个数使其+1,问如何选择这个数,可以使得修改后的数列中的所有数之积的值最大
思路:其实就是选择n-1个数的乘积值加一倍,关键在于选哪一个n-1个数的乘积值,逆向思维就是对于n个数,去掉那个最小值,那么剩下来的n-1个数之积就会最大了,于是就是选择最小的数+1,最终数列之积就是答案了。
1 | |
3. 1D Eraser
https://codeforces.com/contest/1873/problem/D
题意:给定一个只有B和W两种字符的字符串,现在有一种操作可以将一个指定大小的区间(大小为k)中所有的字符全部变为W,问对于这个字符串,至少需要几次上述操作才可以将字符串全部变为W字符
思路:我们直接遍历一边字符串即可,在遍历到B字符的时候,指针向后移动k位,如果是W字符,指针向后移动1位即可,最终统计一下遇到B字符的次数即可。
1 | |
4. ABBC or BACB
https://codeforces.com/contest/1873/problem/G
题意:现在有一个只有A和B两种字符的字符串,有如下两种操作:第一种,可以将AB转化为BC,第二种,可以将BA转化为CB。问最多可以执行上述操作几次
思路:其实一开始想到了之前做过的翻转数字为-1,最后的逻辑是将数字向左右移动,于是这道题就有了突破口了。上述两种操作就可以看做将A和B两种字符交换位置,并且B保持不变,A变为另一种字符C。由于C是无法执行上述操作得到,因此就可以理解为B走过的路就不可以再走了,那么就是说对于一个字符串,最终都会变成B走过的路C。并且只要有B,那么一个方向上所有的A都会被利用转化为C(直到遇到下一个B停止),那么我们就可以将B看做一个独立的个体,他可以选择一个方向上的所有的A并且执行操作将该方向的A全部转化为C,那么在左和右的抉择中,就是要选择A数量最多的方向进行操作,但是如果B的足够多,那就不需要考虑哪个方向了,所有的A都可以获得一次操作机会。现在就转向考虑B需要多少呢,
答案是两种:如果B的数量小于A“块”的数量,其实就是有一块A无法被转化,那么为了让被转化的A数量尽可能的多,就选择A块数量最少的那一块不被转化。如果B的数量>=A块的数量,那么可以保证所有的A都可以被转化为C块,从而最终的答案就是A字符的数量
1 | |
5. Smilo and Monsters
https://codeforces.com/contest/1891/problem/C
题意:给定一个序列,其中每一个元素代表一个怪物群中的怪物的数量。现在有两种操作:
- 选择一个怪物群,杀死其中的一只怪物。同时累加值
x + = 1 x+=1 - 选择一个怪物群,通过之前积累的累加值,一次性杀死当前怪物群中的
只怪物,同时累加值 x x 归零 x x 现在询问杀死所有怪物的最小操作次数
思路:一开始我是分奇偶进行判断的,但是那只是局部最优解,全局最优解的计算需要我们“纵观全局”。
我们可以先做一个假设:假设当前只有一个怪物群,为了最小化操作次数,最优解肯定是先杀死一半的怪物(假设数量为n,则获得累计值x=n),然后无论剩余n个还是n+1个,我们都使用累计值x一次性杀死n个怪物。
现在我们回到原题,有很多个怪物群,易证,最终的最优解也一点是最大化利用操作2,和特殊情况类似,能够利用的一次性杀死的次数就是怪物总数的一半。区别在于:此时不止一个怪物群。那么我们就要考虑累加值如何使用。很容易想到先将怪物群按照数量大小进行排序,关键就在于将累加值从小到大进行使用还是从大到小进行使用。可以发现,对于一个确定的累加值,由于操作2的次数也会算在答案中。那么如果从最小的怪物群开始使用,就会导致操作2的次数变多。因此我们需要从最大值开始进行操作2。
那么最终的答案就是:
- 首先根据怪物数量的总和计算出最终的累加值s(s=sum/2)
- 接着我们将怪物群按照数量进行升序排序
- 然后我们从怪物数量最大的开始进行操作2,即一次性杀死当前怪物群,没进行一次,答案数量+1
- 最后将答案累加上无法一次性杀死的怪物群中怪物的总数
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
6. 通关
https://www.lanqiao.cn/problems/5889/learning/?contest_id=145
声明:谨以此题记录我的第一道正式图论题(存图技巧抛弃了y总的纯数组,转而使用动态数组
vector进行建图)e.g.
2
3
4
5
6struct Node {
int id; // 当前结点的编号
int a; // 属性1
int b; // 属性2
};
vector<Node> G[N];题意:给定一棵树,每个结点代表一个关卡,每个关卡拥有两个属性:通关奖励值
val和可通关的最低价值cost。现在从根节点开始尝试通关,每一个结点下面的关卡必须要当前结点通过了之后才能继续闯关。问应该如何选择通关规划使得通过的关卡数最多?思路:一开始想到的是直接莽bfs,对每一层结点按照cost升序排序进行闯关,然后wa麻了。最后一看正解原来是还不够贪。正确的闯关思路应该是始终选择当前可以闯过的cost最小的关卡,而非限定在了一层上。因此我们最终的闯关顺序是:对于所有解锁的关卡,选择cost最小的关卡进行通关,如果连cost最小的关卡都无法通过就直接结束闯关。那么我们应该如何进行代码的编写呢?分析可得,解锁的关卡都是当前可通过的关卡的所有子结点,而快速获得当前cost最小值的操作可以通过一个堆来维护。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
7. 串门
https://www.lanqiao.cn/problems/5890/learning/?contest_id=145
题意:给定一棵无向树,边权为正。现在询问在访问到每一个结点的情况下最小化行走的路径长度
思路:首先我们不管路径长度的长短,我们直接开始串门。可以发现,我们一点会有访问的起点和终点,那么在起点到终点的这条路上,可能会有很多个分叉,对于每一个分叉,我们都需要进入再返回来确保分叉中的结点也被访问到,那么最终的路径长度就是总路径长度的2倍 - 起点到终点的距离,知道了这个性质后。我们可以发现,路径的总长度是一个定值,我们只有最大化起点到终点距离才能确保行走路径长度的最小值。那么问题就转化为了求解一棵树中,最长路径长度的问题。即求解树的直径的问题。
树的直径:首先我们反向考虑,假设知道了直径的一个端点,那么树的直径长度就是这棵树以当前结点为根的深度。那么我们就需要先确定一个直径的端点。不难发现,对于树中的任意一个结点,距离它最远的一个(可能是两个)结点一定是树的直径的端点。那么问题就迎刃而解了。
为了降低代码量,我们可以设置一个dist数组来记录当前结点到根的距离。
- 在确定直径端点的时候,选择任意一个结点为根节点,然后维护dist数组,最终dist[i~n]中的最大值对应的下标maxi就是直径的一个端点。
- 接着在计算直径长度的时候,以maxi为树根,再来一次上述的维护dist数组的过程,最终dist[1~n]中的最大值就是树的直径的长度
时间复杂度:
O ( n ) O(n)
1 | |
8. Codeforces rating
https://vijos.org/d/nnu_contest/p/1532
题意:现在已知一个初始值R,现在给定了n个P值,选择其中的合适的值,使得最终的
最大 R ′ = 3 / 4 R + 1 / 4 P R'=3/4 R + 1/4 P 思路:首先一点就是我们一定要选择P比当前R大的值,接下来就是选择合适的P使得最终迭代出来的R’最大。首先我们知道,对于筛选出来的比当前R大的P集合,任意选择其中的一个P,都会让R增大,但是不管增加多少都是不会超过选择的P。那么显然,如果筛选出来的P集合是一个递增序列,那么就可以让R不断的增加。但是这一定是最大的吗?我们不妨反证一下,现在我们有两个P,分别为x,y,其中
。 x < y x<y 那么按照上述思路,首先就是
R ′ = 3 4 R + 1 4 x ( R ′ < x ) R'=\frac{3}{4}R+\frac{1}{4}x(R'<x) 接着就是
R 1 ′ ′ = 3 4 R ′ + 1 4 y ( R 1 ′ ′ < y ) = 9 16 R + 3 16 x + 1 4 y R''_1=\frac{3}{4}R'+\frac{1}{4}y(R''_1<y)=\frac{9}{16}R+\frac{3}{16}x+\frac{1}{4}y 反之,首先选择一个较大的P=y,再选择一个较小的P=x,即首先就是
R ′ = 3 4 R + 1 4 y ( R ′ < y ) R'=\frac{3}{4}R+\frac{1}{4}y(R'<y) 此时我们还不一点可以继续选择x,因为此时的R’可能已经超过了x的值,那么我们按照最优的情况计算,可以选择x,那么就是
R 2 ′ ′ = 3 4 R ′ + 1 4 x ( R 2 ′ ′ < x ) = 9 16 R + 3 16 y + 1 4 x R''_2=\frac{3}{4}R'+\frac{1}{4}x(R''_2<x)=\frac{9}{16}R+\frac{3}{16}y+\frac{1}{4}x 可以发现
R 2 ′ ′ − R 1 ′ ′ = 1 16 ( x − y ) < 0 R''_2-R''_1=\frac{1}{16}(x-y)<0 即会使得最终的答案变小。因此最优的策略就是按照增序进行叠加计算
==注意点:==
四舍五入的语句
cout << (int)(res + 0.5) << "\n";
1 | |
9. 货运公司
https://www.acwing.com/problem/content/5380/
题意:给定
个运货订单,每个订单需要运送一定量的货物,同时给予一定量的报酬。现在有 n n 个卡车进行运送,每个卡车有运送容量。需要合理规划卡车的装配,使得最终获得的总报酬最大。有以下约束条件: k k
- 每一个订单只能用一辆货车运送
- 每一辆货车只能运送不超过最大容量的货物
- 每一辆货车只能运送一次
- 每一辆货车在装得下的情况下只能装运一个订单
思路:一开始尝试采用 01 背包的思路,但是题目中货物是否可以被运送是取决于卡车的装载的。思考无果后考虑贪心。考虑一般情况
为了让总收益最大,很显然报酬越多,就越优先选择该订单
在报酬一致时,货物量越少,就越优先选择该订单
按照上述规则对订单排序后,我们需要安排合理的货车进行运输。我们优先将运输量小的货车安排给合适的订单。因为运输量大的货车既可以满足当前订单,同样也满足后续的订单,那么为了最大化增加利润,就需要在运输量小的货车满足当前订单时,保留运输量大的货车用于后续的订单。我们可以画一个图进一步理解为什么这么安排货车进行运输:
 图例:我们按照上述红笔的需要进行货车的选择进行运输
图例:我们按照上述红笔的需要进行货车的选择进行运输如果红色序号顺序变掉了,则就不能将上述图例中的 6 个订单全部运输了
时间复杂度
O ( n k ) O(nk)
1 | |
10. 部分背包问题
https://www.luogu.com.cn/problem/P2240
- 题意:给定一组物品,每一个物品有一定的重量与价值,现在给定一个背包总承重,需要从中选择合适的物品进行装载,使得最终装载的物品的总价值最大。现在规定每一个物品可以进行随意分割,按照单位重量计算价值
- 思路:考虑一般情况。很显然,如果不说可以随意分割,那就是一个 01 背包,既然说了可以随意分割,那就直接贪心选择即可,按照单位重量的价值降序进行选择
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
11. 排队接水
https://www.luogu.com.cn/problem/P1223
题意:贪心经典,排队接水,每一个人都有一个打水时间,现在询问如何排队能够使得平均等待时间最短
思路:考虑一般情况。注意问的是平均等待时间,如果是打完水总花费时间那就是一个定值,即所有人打水的时间总和。现在为了让平均等待时间最短,我们的第一反应应该是,在人多的时候让打水时间短的先打,人少的时候让打水时间长的再打,那么很显然就是按照打水时间的升序进行排队。为了证明这个结论,我们采用数学归纳法,如下,对于一个排队序列来说,我们将其中的两个顺序进行颠倒,计算结果得到让打水时间短的排在前面更优,进而推广到一般情况,于是按照打水时间升序进行打水的策略是最优的。证毕
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
12. 线段覆盖
https://www.luogu.com.cn/problem/P1803
- 题意:给定一个数轴和数轴上的 n 个线段,现在需要从中选出尽可能多的 k 个线段,使得线段之间两两不相交,问 k 最大是多少
- 思路:绞尽脑汁想着各种情况进行分类讨论,什么包含、相交、相离,但是都忽视了最重要的一点,那就是一开始应该选择线段。即考虑边界,对于最左侧我们应该选择哪一条线段呢?答案是最左侧的右端点最靠左的那一条线段,这样子后续的线段才能有更多的摆放空间
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
13. 小A的糖果
https://www.luogu.com.cn/problem/P3817
- 题意:给定一个序列,现在每次可以选择序列中的某个数进行减一操作,问最少需要减多少可以使得序列中相邻两个元素之和不超过规定的数值 x
- 思路:同 T12 的思路展开,考虑边界,我们直接从任意的一个边界开始思考,假设从左边界开始考虑。为了让左边界满足,那么 a[1] 与 a[2] 之和就需要满足条件,为了后续可以尽可能少的进行减一操作,很显然我们最好从两个数的右边的数开始下手,于是贪心的结果就有了
- 时间复杂度:
O ( n ) O(n)
1 | |
15. 陶陶摘苹果(升级版)
https://www.luogu.com.cn/problem/P1478
- 题意:现在有 n 个苹果,含有高度和消耗体力值两个属性,现在你有一个最大高度以及总体力值,每次只能摘高度值不超过最大高度的苹果且会消耗相应的体力值。问最多可以摘多少个苹果
- 思路:既然是想要摘的苹果尽可能多,那么高度都是浮云,体力值才是关键。为了摘得尽可能多的苹果,自然是消耗体力越少越优先摘。于是按照消耗体力值升序排序后,扫描一遍即可计数
- 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
16. [NOIP2018 提高组] 铺设道路
https://www.luogu.com.cn/problem/P5019
题意:给定一个序列,每次可以选择一个连续的区间使得其中的所有数 -1,前提是区间中的数都要 > 1,问最少选择几次区间可以将所有的数全部都减到 0
思路:很显然的一个贪心思路就是,对于一个数,左右两侧均呈现递减的趋势,那么这个区间的选择数就是这个最大的数的值。但是这不符合代码逻辑,我们尝试从端点开始考虑。为了更好的理解,我们从递推的角度进行推演。假设填平前 i 个数花费的选择次数为 f[i],那么对于第一个数 a[1],我们一定需要花费 a[1] 次选择来将其减到零,于是 f[1] = a[1];对于后续的数而言,可以发现
- 如果 a[i] > a[i-1],那么之前的选择没有完全波及当前的数,还需要一定的次数来将其减到零,于是
f[i] = f[i-1] + a[i] - a[i-1]- 如果 a[i]
a[i-1],那么当前的数值一定会被之前的选择“波及”而直接减到零,于是 ≤ \le f[i] = f[i-1]从递推的角度理解之后我们直接滚动一遍数组记录増势即可
时间复杂度:
O ( n ) O(n)
1 | |
17. [USACO1.3] 混合牛奶 Mixing Milk
https://www.luogu.com.cn/problem/P1208
- 题意:现在需要收集 need 容量的牛奶,同时有 n 个农户提供奶源,每一个商户的奶源有一定的数量与单价,问如何采购可以在满足需求 need 的情况下成本最低化
- 思路:很显然单价越低越优先采购
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
18. [NOIP2007 普及组] 纪念品分组
https://www.luogu.com.cn/problem/P1094
- 题意:给定 n 个数,问如何分组可以使得在每一组之和不超过定值 lim 且每一组最多两个数的情况下,分得的组数最少
- 思路:对序列没有要求,显然直接排序然后从一端开始考虑。首先有一个概念就是,为了尽可能的减少分得的组数,那么一定想要每一组分完后距离 lim 的差距越小越好。我们将 n 个数降序排序后,从最大值开始考虑,对于当前的数,为了找到一个数与当前数之和尽可能接近 lim,从贪心的角度来说一定是从当前数之后开始寻找那个配对的数从而使得两数之和与 lim 的差距最小,那么时间复杂度就是
。但是由于题目说了最多只有两个数,我们不妨换一种寻找配对数的策略,可以从原始的寻找方法得到启发,可以发现,原始的寻找配对数的方法中,如果找到的那个配对数可以与当前数之和不超过 lim 且之和尽可能的大,那么这个寻找到的配对数也一定可以和当前数的下一个数进行配对。由于我们一组只能有两个数,因此我们不用考虑两数组合之后比 lim 小的数尽可能的小,只需要考虑两个数能否组合即可,因此我们直接双指针进行寻找配对数操作即可 O ( n 2 ) O(n^2) - 时间复杂度:
O ( n ) O(n)
1 | |
19. 跳跳!
https://www.luogu.com.cn/problem/P4995
题意:给定 n 个数,每一个数代表一个高度,现在有一只青蛙从地面(高度为 0)开始起跳,每一个数字只能被跳上去一次。问如何设定跳数顺序 h[],可以使得下式尽可能的大
∑ i = 1 n ( h i − h i − 1 ) 2 \sum_{i=1}^n (h_i-h_{i-1})^2 思路:题目意思其实就是让每一次跳跃的两个高度之差尽可能的大。那么一个贪心的思路就是从地面跳到最高,再从最高跳到次低,接着从次低跳到次高,以此类推得到的结果就是最优解,为了证明我们可以用数学归纳法,假设当前只有两个高度可以选择,那么肯定是先跳高的再跳低的;假设当前有三个高度可以选择,那么可以证明先从地面跳到最高处,再跳到最低处,最后跳到第二高的方法得到的值最大
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
20. 安排时间
https://www.acwing.com/problem/content/5466/
- 题意:给定 n 个时间段处理餐厅事务,m 个用餐预定信息,含有三个信息分别为订单发起时间,订单需要准备的时间,客人来用餐时间。问如何安排每一个时间段,可以让所有的用户得到正常的服务。如果不能全部满足则输出 -1
- 思路:玄学贪心,先到的用户先做它的菜
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
21. [NOIP2004 提高组] 合并果子
https://www.luogu.com.cn/problem/P1090
- 题意:给定 n 个数,现在需要将其两两合并为最终的一个数,每次合并的代价是两个数之和,问如何对这些数进行合并可以使得总代价最小
- 思路:很显然一共需要合并 n-1 次。那么我们从三个物品开始考虑,然后使用数学归纳法推导到 n 个数。对于三个物品,很显然先将两个物品进行合并,再将这个结果与最大的数进行合并方案时最优的。那么推广到 n 个数,我们只需要每次合并当前局面中最小的两个数即可
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
22. 删数问题
https://www.luogu.com.cn/problem/P1106
- 题意:给定一个数字字符串长度为 n,现在需要选择其中的 m 位数,使得这 m 位组成的数最小是多少 (m=n-k)
- 思路:我们从一端考虑问题。为了组成的数尽可能的小,我们希望从首位开始就尽可能的小,同时如果有重复的数字,就选择最左侧的,剩余的数字留给后续的位数继续选择。有一个需要注意的点就是选择每一位的数字时,范围的约束,我们假设需要从 10 位的数字串中选择 3 位,那么我们第一次选择时需要在 0-7位中选择一位,第二次选择在 上次选择的下一个位置到第8位中选择一位,以此类推进行贪心选择
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
23. 截断数组
https://www.acwing.com/problem/content/5483/
题意:定义平衡数组为奇偶数数量相同的数组,现在给定一个平衡数组,和一个总成本数,最多可以将原数组截成多少截子平衡数组,且截断代价总和不超过总成本,截断代价计算公式为
∣ a i − a i + 1 ∣ |a_i-a_{i+1}| 思路:我们直接枚举所有的可以被截断的位置,统计所有的代价值,然后根据成本总数按降序枚举代价值即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
24. 修改后的最大二进制字符串
https://leetcode.cn/problems/maximum-binary-string-after-change/description/
题意:给定一个仅由01组成的字符串,现在可以执行下面两种操作任意次,使得最终的字符串对应的十进制数值最大,给出最终的字符串
00 → 10 00 \to 10 10 → 01 10 \to 01 思路:
- 有点像之前做的翻转转化为平移的问题,事实确实如此。首先需要确定一点就是:如果字符串起始有连续的1,则保留,因为两种操作都是针对0的。接着就是对从第一个0开始的尾串处理的思路
- 对于尾串而言,我们自然希望1越多、越靠前越好,但是第二种操作只能将1向后移,第一种操作又必须要连续的两个0,因此我们就产生了这样的贪心思路:将所有的1通过操作二移动到串尾,接着对尾串的开头连续的0串执行第二种操作,这样就可以得到最大数值的二进制串
时间复杂度:
O ( n ) O(n)
1 | |
25. 子序列最大优雅度
https://leetcode.cn/problems/maximum-elegance-of-a-k-length-subsequence/
标签:反悔贪心
题意:给定长度为 n 的物品序列,现在需要从中寻找一个长度为 k 的子序列使得子序列的总价值最大,给出最终的最大价值。一个序列的价值定义为每个物品的 本身价值之和 + 物品种类数的平方
思路:我们采用反悔贪心的思路。首先按照物品本身价值进行降序排序并选择前 k 个物品作为集合 S,然后按顺序枚举剩下的物品进行替换决策。我们记每个物品有一个「本身价值」,集合 S 有一个「种类价值」。那么就会遇到下面两种情况:
- 第 i 个物品对应的种类存在集合 S 中。此时该物品「一定不选」,因为无论当前物品替代集合中的 S 哪一个物品,本身价值的贡献会下降、种类价值的贡献保持不变。
- 第 i 个物品对应的种类不在集合 S 中。此时该物品一定选择吗?不一定。有两种情况:
- 集合 S 没有重复种类的物品。此时该物品「一定不选」,同样的,无论当前物品替代集合中的 S 哪一个物品,本身价值的贡献会下降、种类价值的贡献保持不变。
- 集合 S 存在重复种类的物品。此时该物品「一定选」,因为一定可以提升种类价值的贡献,至于减去本身价值的损失后是否使得总贡献增加,并不具备可能的性质,只能每次替换物品时更新全局答案进行记录。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
1 | |
【按位贪心/分类讨论】
https://www.acwing.com/problem/content/1000/
题意:给定
个运算数和对应的 n n 个操作,仅有 n n &, |, ^三种。现在需要选择一个数使得 n u m ∈ [ 0 , m ] num \in [0,m] 经过这 n u m num 个二元运算后得到的结果 n n 最大。给出最终的 r e s res 。 r e s res 思路:首先不难发现这些运算操作在二进制位上是相互独立的,没有进位或结尾的情况,因此我们可以「按二进制位」单独考虑。由于运算数和
均 m m ,因此我们枚举 ≤ 1 0 9 \le 10^9 对应的二进制位。接下来我们单独考虑第 [ 0 , 30 ] [0,30] 位的情况,显然的 i i 的第 n u m num 位可以取 i i 也可以取 1 1 ,对应的 0 0 的第 r e s res 位可以取 i i 也可以取 1 1 。有以下 0 0 种运算情况: 2 2 2^2
$\text{num 的第 i 位填 1 res 第 i 位的情况}$ → \to $\text{num 的第 i 位填 0 res 第 i 位的情况}$ → \to 选择方案 情况一 1 → 0 1 \to 0 0 → 0 0 \to 0 num 填 0,res 填 0 情况二 1 → 0 1 \to 0 0 → 1 0 \to 1 num 填 0,res 填 1 情况三 1 → 1 1 \to 1 0 → 0 0 \to 0 待定 情况四 1 → 1 1 \to 1 0 → 1 0 \to 1 num 填 0,res 填 1 选择方案时我们需要考虑两个约束,
不能超过 n u m num , m m 尽可能大,因此有了上述表格第四列的贪心选择结果。之所以情况三待定是因为其对两种约束的相互矛盾的,并且其余情况没有增加 r e s res ,即对 n u m num 上限的约束仅存在于情况三。假设有 n u m num 位是上述情况三,那么显然的其余位枚举顺序是随意的,因为答案是固定的。对于 k k 个情况三,从贪心的角度考虑,我们希望 k k 尽可能大,那么就有「高位能出 r e s res 就出 1 1 」的结论。因此我们需要从高位到低位逆序枚举这 1 1 个情况三,由于其他位枚举顺序随意,因此总体就是从高位到低位枚举。 k k 时间复杂度:
O ( n log m ) O(n \log m)
1 | |
整数问题。
【质数】Divide and Equalize
题意:给定
个数,问能否找到一个数 n n ,使得 n u m num n u m n = ∏ i = 1 n a i num^n = \prod_{i=1}^{n}a_i 原始思路:起初我的思路是二分,我们需要寻找一个数使得n个数相乘为原数组所有元素之积,那么我们预计算出所有数之积,并且在数组最大值和最小值之间进行二分,每次二分出来的数计算n次方进行笔比较即可。但是有一个很大的问题是,数据量是
,而数字最大为 1 0 4 10^4 ,最大之积为 1 0 6 10^6 吗?不是!最大之和才是,最大之积是 1 0 10 10^{10} 1 0 6 × 1 0 4 10^{6\times10^4} 最终思路:我们可以将选数看做多个水池匀水的过程。现在每一个水池的水高都不定,很显然我们一定可以一个值使得所有的水池的高度一致,即
。但是我们最终的数字是一个整数,显然不可以直接求和然后除以n,那么应该如何分配呢?我们知道水池之所以可以直接除以n,是因为水的最小分配单位是无穷小,可以随意分割;而对于整数而言,最小分配单位是什么呢?答案是质因子!为了通过分配最小单位使得最终的“水池高度一致”,我们需要让每一个“水池”获得的数值相同的质因子数量相同。于是我们只需要统计一下数组中所有数的质因子数量即可。如果对于每一种质因子的数量都可以均匀分配每一个数(即数量是n的整数倍),那么就一定可以找到这个数使得 ∑ i = 1 n a i n \frac{\sum_{i=1}^{n}a_i}{n} n u m n = ∏ i = 1 n a i num^n = \prod_{i=1}^{n}a_i
1 | |
【整除】Deja Vu
https://codeforces.com/contest/1891/problem/B
题意:给点序列 a 和 b,对于 b 中的每一个元素
,如果 a 中的元素 b i b_i 能够整除 a j a_j ,则将 2 b i 2^{b_i} 加上 a j a_j 。给出最后的 a 序列 2 b i − 1 2^{b_i - 1} 思路一:暴力枚举。
我们很容易就想到暴力的做法,即两层循环,第一层枚举 b 中的元素,第二层枚举 a 中的元素,如果 a 中的元素能够整除 2 的
次方,就将 a 中相应的元素加上一个值即可。但是时间复杂度肯定过不了,考虑优化。 b i b^i 时间复杂度:
O ( n m ) O(nm) 思路二:整除优化。
现在我们假设a中有一个数
是 a j a_j 的整数倍(其中 2 b i 2^{b_i} 是b序列中第一个枚举到的能够让 b i b_i 整除的数),那么就有 a i a_i ,那么 a j = k 2 b i ( k = 1 , 2 , . . . , ) a_j = k2^{b_i}(k=1,2,...,) 就要加上 a j a_j ,于是 2 b i − 1 2^{b_i-1} 就变为了 a j a_j 。此后 k 2 b i + 2 b i − 1 = ( 2 k + 1 ) 2 b i − 1 k2^{b_i}+2^{b_i-1}=(2k+1)2^{b_i-1} 就一定是 a j a_j 的倍数。因此我们需要做的就是首先找到b序列中第一个数x,能够在a中找到数是 2 t ( t ∈ [ 1 , b i − 1 ] ) 2^t(t\in \left[ 1,b_i-1 \right]) 的整数倍。这一步可以这样进行:对于 a中的每一个数,我们进行30次循环统计当前数是否是 2 x 2^x 的倍数,如果是就用哈希表记录当前的 2 i 2^i 。最后我们在遍历寻找 x 时,只需要查看当前的 x 是否被哈希过即可。接着我们统计b序列中从x开始的严格降序序列c(由题意知,次序列的数量一定 i i 30,因为b序列中数值的值域为 ≤ \le )。最后我们再按照原来的思路,双重循环 a 序列和 c 序列即可。 [ 1 30 ] [1~30] 时间复杂度:
O ( 30 n ) O(30n)
1 | |
【组合数学】序列数量
https://www.acwing.com/problem/content/5571/
题意:给定
个苹果,将其分给 i ( i = 1 , 2 , ⋯ , n ) i(i=1,2,\cdots,n) 个人,问一共有多少种分配方案,给出结果对 m m 取模的结果 1 0 6 + 3 10^6+3 思路:整数分配问题。我们采用隔板法,隔板法相关例题见这篇博客:https://www.acwing.com/solution/content/241669/。下面开始讲解
利用隔板法推导结果。首先我们考虑当前局面,即只有 i 个苹果的情况下的方案数。于是题目就是 i 个苹果分给 m 个人,允许分到 0 个。于是借鉴上述链接中“少分型”的思路,先借 m 个苹果,那么此时局面中就有 i+m 个苹果,现在就等价于将 i+m 个苹果分给 m 个人,每人至少分得 1 个苹果。(分完以后每个人都还回去就行了),此时的隔板操作就是”标准型”,即 i+m 个苹果产生 i+m-1 个间隔,在其中插 m-1 块板,从而将划分出来的 m 个部分分给 m 个人。此时的划分方案就是
,那么对于所有的 i,结果就是 C i + m − 1 m − 1 C_{i+m-1}^{m-1}
∑ i = 1 n C i + m − 1 m − 1 = C m m − 1 + C m + 1 m − 1 + ⋯ + C n + m − 1 m − 1 = C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n = ( − C m 0 + C m 0 ) + C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n = − C m 0 + ( C m 0 + C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n ) = − 1 + ( C m + 1 1 + C m + 1 2 + ⋯ + C n + m − 1 n ) = − 1 + ( C m + 2 2 + ⋯ + C n + m − 1 n ) = − 1 + C n + m n \begin{aligned}\sum_{i=1}^n C_{i+m-1}^{m-1} &= C_{m}^{m-1} + C_{m+1}^{m-1} + \cdots + C_{n+m-1}^{m-1} \\&= C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\&= (-C_{m}^{0}+C_{m}^{0})+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\&= -C_{m}^{0}+(C_{m}^{0}+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+(C_{m+1}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+(C_{m+2}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+C_{n+m}^n\end{aligned} 利用乘法逆元计算组合数。结果已经知道了,现在如何计算上述表达式呢?由于
超过了常规递推的组合数计算方法内存空间,因此我们采用乘法逆元的思路计算。值得一提的是,本题在计算某个数关于 n × m n\times m 1e6+3的乘法逆元时,不需要判断两者是否互质,因为1e6+3是一个质数,并且数据范围中的数均小于1e6+3,因此两数一定互质,可以直接使用费马小定理计算乘法逆元时间复杂度:
O ( n log 1 e 6 ) O(n\log 1e6)
1 | |
【哈希】分组
https://www.acwing.com/problem/content/5182/
存储不想同组和想同组的人员信息:存入数组,数据类型为一对字符串
存储所有的组队信息:存入哈希表,数据类型为“键:字符串”“值:一对字符串”
想要知道最终的分组情况,只需要查询数组中的队员情况与想同组 or 不想同组的成员名字是否一致即可
时间复杂度
,空间复杂度 O ( n ) O(n) O ( n l e n ( n a m e ) ) m a x O(n\ len(name))_{max}
1 | |
【哈希】海港
https://www.luogu.com.cn/problem/P2058
- 题意:给定 n 艘船只的到达时间、载客信息(载客人数和每一个客人的国籍),现在需要知道对于每一艘抵达的船只,前 24 小时中抵达的客人的国籍总数
- 思路:本题思路很简单,就是一个队列的应用以及哈希客人国籍的过程。由于船只抵达的时间是顺序增加的,故每抵达一艘船只,就对新来的客人国籍进行哈希,为了计算前 24 小时的情况,需要对船只抵达队列进行删减,即只保留 24 小时以内的船只抵达信息。对于删除的船只信息,需要将这些船只上的客人国籍信息从哈希表中删除,故每一艘船只的访问次数为 2。
unordered_map补充:在进行哈希统计时。为了判断当前 24 小时内客人国籍数,在删除哈希记录时,为了判断是否将当前国籍的游客全部删除时,需要统计哈希表中某个国籍是否减为了 0,我用了.count(x)内置方法,但这是不正确的,因为我想要统计的是 值 是否为 0,而.count(x)统计的是哈希表中 x 这个 键 的个数,而unordered_map中是没有重复的键的,故.count(x)方法只会返回 0 或 1,返回 0 就表示当前哈希表中没有 x 这个键,返回 1 就表示哈希表中有 x 这个键,但是有这个键不代表对应的值就存在,可能是x: 0的情况,即键存在,但是值记录为 0- 时间复杂度:
- 即两倍的所有游客数 O ( 2 ∑ x i ) O(2 \sum x_i)
1 | |
【哈希】Cities and States S
https://www.luogu.com.cn/problem/P3405
题意:给定 n 个字符串,每一个字符串归属一个集合,现在需要统计字符串与集合名相反相等的对数
思路:很显然的哈希计数。难点有两个,如何哈希?如何计数?哈希可以采用扩展字符的方法进行,即第一个字符乘某一个较大的质数再加上第二个字符。此处采用一种较为巧妙的方法,直接将两个字符串与集合名加起来进行唯一性哈希,降低编码难度。计数有两种方式,第一种就是全部哈希结束之后,再遍历哈希表进行统计,最后将结果除二即可。第二种就是边哈希边计数,遇到相反相等的就直接计数,这样就不会重复计数了,也很巧妙
时间复杂度:
O ( n ) O(n)
1 | |
【哈希/枚举/思维】Torn Lucky Ticket
https://codeforces.com/contest/1895/problem/C
题意: 给定一个长度为 n 的字符串数组 nums, 数组的每一个元素长度不超过 5 且仅由数字组成. 问能找到多少对
可以使得拼接后的 ( i , j ) (i,j) 长度为偶数且左半部分的数字之和与右半部分的数字之和相等. n u m s [ i ] + n u m s [ j ] nums[i]+nums[j] 思路:
首先最暴力的做法就是
枚举,所有的 O ( n 2 ) O(n^2) 然后 check 合法性. ( i , j ) (i,j) 尝试优化掉第二层的枚举循环. 对于第二层循环, 我们就是要寻找合适的
并和当前的 n u m s [ j ] nums[j] 拼接. 显然我们可以通过扫描当前的 n u m s [ i ] nums[i] 并 n u m s [ i ] nums[i] 的计算出所有 O ( 1 ) O(1) 且可以和 l e n ( n u m s [ j ] ) ≤ l e n ( n u m s [ i ] ) len(nums[j])\le len(nums[i]) 匹配的字符串的 n u m s [ i ] nums[i] [长度][数字和]信息, 只需要一个二维数组预存储每一个字符串的 长度 数字和 信息即可.那么对于
的情况如何统计呢. 显然此时我们没法 l e n ( n u m s [ j ] ) > l e n ( n u m s [ i ] ) len(nums[j])> len(nums[i]) 的检查 O ( 1 ) O(1) 的合法性. 不妨换一个角度, 当我们枚举 n u m s [ i ] + n u m s [ j ] nums[i]+nums[j] 时: n u m s [ i ] nums[i]
统计右侧拼接长度更大的 nums[j] 的合法情况数 ⟺ 统计左侧拼接长度更小的 nums[j] 的合法情况数 \text{统计右侧拼接长度更大的 nums[j] 的合法情况数} \iff \text{统计左侧拼接长度更小的 nums[j] 的合法情况数} 于是合法情况数就可以表示为
, 其中第一种情况 ∑ i = 0 n − 1 [ cond 1 ( n u m s [ i ] ) + cond 2 ( n u m s [ i ] ) ] \displaystyle \sum_{i=0}^{n-1}\big[\text{cond}_1(nums[i])+\text{cond}_2(nums[i])\big] 就是统计右侧拼接长度更小的字符串数量, 第二种情况 cond 1 \text{cond}_1 就是统计左侧拼接长度更小的字符串数量. 这两步可以同时计算. cond 1 \text{cond}_1 时间复杂度:
O ( n ) O(n)
1 | |
【拓扑】有向图的拓扑序列
https://www.acwing.com/problem/content/850/
题意:输出一个图的拓扑序,不存在则输出-1
思路:
- 首先我们要知道拓扑图的概念,感官上就是一张图可以从一个方向拓展到全图,用数学语言就是:若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列
- 接着我们就想要寻找这样的序列 A 了,可以发现对于每一个可扩展的点,入度一定为0,那么我们就从这些点开始宽搜,将搜到的点的入度-1,即删除这条边,直到最后。如果全图的点的入度都变为了0,则此图可拓扑
时间复杂度:
O ( n + m ) O(n+m)
1 | |
【基环树/拓扑】Mad City🔥
https://codeforces.com/contest/1873/problem/H
tag:基环树、拓扑排序
题意:给定一个基环树,现在图上有两个点,分别叫做A,B。现在B想要逃脱A的抓捕,问对于给定的局面,B能否永远逃离A的抓捕
思路:思路很简单,我们只需要分B所在位置的两种情况讨论即可
- B不在环上:此时我们记距离B最近的环上的那个点叫
,我们需要比较的是A到tag点的距离 t a g tag 和B到tag的距离 d A d_A ,如果 d B d_B ,则一定可以逃脱,否则一定不可以逃脱 d B < d A d_B < d_A - B在环上:此时我们只需要判断当前的A点是否与B的位置重合即可,如果重合那就无法逃脱,反之B一定可以逃脱。
代码实现:
- 对于第一种情况,我们需要找到tag点以及计算A和B到tag点的距离,
时间复杂度:
1 | |
【二分图】染色法判定二分图
https://www.acwing.com/problem/content/862/
题意:给定一个无向图,可能有重边和自环。问是否可以构成二分图。
二分图的定义:一个图可以被分成两个点集,每个点集内部没有边相连(可以不是连通图)
思路:利用染色法,遍历每一个连通分量,选择连通分量中的任意一点进行染色扩展
- 如果扩展到的点没有染过色,则染成与当前点相对的颜色
- 如果扩展到的点已经被染过色了且染的颜色和当前点的颜色相同,则无法构成二分图(奇数环)
时间复杂度:
O ( n + e ) O(n+e)
1 | |
【最小生成树】Kruskal算法求最小生成树
https://www.acwing.com/problem/content/861/
题意:给定一个无向图,可能含有重边和自环。试判断能否求解其中的最小生成树,如果可以给出最小生成树的权值
思路:根据数据量,可以发现顶点数很大,不适用
算法,只能用 P r i m Prim 算法,下面简单介绍一下该算法的流程 K r u s k a l Kruskal
- 自环首先排除 - 显然这条边连接的“两个”顶点是不可能选进
的 M S T MST - 首先将每一个结点看成一个连通分量
- 接着按照权值将所有的边升序排序后,依次选择
- 如果选出的这条边的两个顶点不在一个连通分量中,则选择这条边并将两个顶点所在的连通分量合并
- 如果选出的这条边的两个顶点在同一个连通分量中,则不能选择这条边(否则会使得构造的树形成环)
- 最后统计选择的边的数量
进行判断即可 n u m num
,则可以生成最小生成树 n u m = n − 1 num=n-1 ,则无法生成最小生成树 n u m < n − 1 num<n-1 - 时间复杂度:
- 因为最大的时间开销在对所有的边的权值进行排序上 O ( e log e ) O(e\log e)
C++
1 | |
Python
1 | |
JavaScript
1 | |
【最小生成树】Prim算法求最小生成树
https://www.acwing.com/problem/content/860/
题意:给定一个稠密无向图,有重边和自环。求出最小生成树
思路:根据题目的数据量,可以使用邻接矩阵存储的方法配合
算法求解最小生成树,下面给出该算法的流程 P r i m Prim
- 首先明确一下变量的定义:
g[i][j]为无向图的邻接矩阵存储结构MST[i]表示号点是否加入了 i i 集合 M S T MST d[i]表示i号点到集合的最短边长度 M S T MST - 自环不存储,重边只保留最短的一条
- 任选一个点到集合
中,并且更新 M S T MST 数组 d d - 选择剩余的
个点,每次选择有以下流程 n − 1 n-1
- 找到最短边,记录最短边长度
和相应的在 e e 集合中对应的顶点序号 U − M S T U-MST v v - 将
号点加入 v v 集合,同时根据此时选出的最短边的长度来判断是否存在最小生成树 M S T MST - 根据
号点,更新 v v 数组,即更新在集合 d d 中的点到 U − M S T U-MST 集合中的点的交叉边的最短长度 M S T MST - 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【最短路】Dijkstra求最短路 🔥
朴素版 - https://www.acwing.com/problem/content/851/
堆优化 - https://www.acwing.com/problem/content/852/
题意:给定一个正边权的有向图,可能存在重边与自环,问
号点到 1 1 号点的最短路径长度是多少,如果不可达就输出 n n 。 − 1 -1 思路一:朴素版。点数
,边数 1 ≤ n ≤ 500 1\le n \le 500 1 ≤ m ≤ 1 0 5 1 \le m\le 10^5
思路:根据数据量,我们采用邻接矩阵的方式存储「点少边多」的稠密图。我们定义
d[i]数组表示起点到i号点的最短距离。先将起点放入SPT (Shortest Path Tree)集合,然后更新所有V-SPT中的点到SPT集合的最短路径长度。接着循环n-1次迭代更新剩余的n-1个点,每次迭代的过程中,首先选择距离起点最近的点vex,然后将该点加入SPT集合,最后利用该点更新V-SPT集合中和该点有连边的点到起点的最短距离。最终的d[end]就是起点start到终点end的最短距离。总结:算法整体采用贪心与动态规划的思路。与
算法仔细比对可知,其中的贪心过程几乎一致,即每次选择加入 SPT 集合的点均为当前局面 Prim \text{Prim} V-SPT集合中距离起点最近的点。而动态规划的过程体现在,在求解出集合V-SPT中到集合STP最短距离的点vex之后,利用该点对「在V-SPT集合且和 vex 点有连边的点i」更新d[i]的过程。更新前的状态都是在之前的子结构下的最优解。时间复杂度:
O ( n 2 ) O(n^2) 思路二:堆优化。点数
,边数 1 ≤ n ≤ 1.5 × 1 0 5 1\le n \le 1.5 \times 10^5 1 ≤ m ≤ 1.5 × 1 0 5 1 \le m \le 1.5 \times 10^5
思路:根据数据量,我们采用邻接表的方式存储「点多边少」的稀疏图。如果采用上述朴素 Dijkstra 算法进行求解必然会因为点数过多而超时,因此我们利用数据结构「堆」进行时间开销上的优化。不难发现朴素 Dijkstra 算法在迭代过程中主要有三部分:
- 选择距离起点最近的点
vex。因为需要枚举所有的顶点,因此总的时间复杂度为O ( n 2 ) O(n^2) - 将该点加入
SPT集合。因为只是简单的打个标记,因此总的时间复杂度为O ( n ) O(n) - 利用该点更新
V-SPT集合中和该点相连的点到起点的最短距离。因为此时枚举的是该点所有的连边,而邻接表的图存储方式无法进行重边的删除,因此最坏情况下会枚举所有的边,时间复杂度为O ( m ) O(m) 时间复杂度:
朴素版C++:
1 | |
朴素版Python:
1 | |
堆优化版C++:
1 | |
【最短路】Floyd求最短路
https://www.acwing.com/problem/content/856/
题意:给定一个稠密有向图,可能存在重边与自环,给出多个询问,需要给出每一个询问的两个点之前的最短路径长度
思路:我们采用动态规划的思路。在此使用多阶段决策的方法,即每一个路径状态为选择
个点的情况下的最短路径长度 1 → k 1\to k
- 状态表示:
f[k][i][j]表示在前个顶点中进行选择(中转), k k 号点到 i i 号点的最短路径长度 j j - 状态转移:对于第
个顶点,我们可以选择中转,也可以不中转。 k k
- 对于不选择中转的情况:
f[k][i][j] = f[k-1][i][j]- 对于可选择中转的情况:
f[k][i][j] = f[k-1][i][k] + f[k-1][k][j]- 在其中取最小值即可,但是有一个注意点:对于第二种情况,选择是有一个约束的:即如果选择了
号点进行转移的话,那么 k k 号点到 i i 号点以及 k k 号点到 k k 号点都是需要有路径可达的,从而可以选择最小距离 j j - 初始化:即选择 0 个站点进行中转时,即
f[0][i][j]的情况中,
- 如果
号点与 i i 号点自环,则取 j j 0 0 - 如果
号点与 i i 号点之间有边,则取重边的最小值 j j - 如果
号点与 i i 号点之间无边,则初始化为正无穷 j j - 答案状态:对于
号点到 a a 号点之间的最小路径长度,就是 b b f[n][a][b]- 时间复杂度:
O ( n 3 ) O(n^3) - 空间复杂度:
O ( n 3 ) O(n^3) 空间优化推导:我们尝试优化掉记忆数组的第一维度
对于不选择的情况:由于决策局面
是从前往后枚举,故当前状态 k k f[k][i][j]可以直接依赖于已经更新出来且不会被当前状态之后的状态再次覆盖的最优子结构f[i][j]。即上一个局面的选择情况,就是不选择第个顶点的情况 k k 对于选择的情况:如果删除第一维度,我们担心的是当前状态
f[k][i][j]依赖的两个状态f[i][k]与f[k][j]会不会被后续覆盖掉,即我们不确定f[i][k]与f[k][j]是否是当前第 k 个局面的最优子结构。尝试推导:为了确定
f[i][k]与f[k][j]是否是当前第个局面的最优子结构,其实就是确定对于当前第 k k 个局面,这两个状态会不会在当前状态 k k f[i][j]之后被更新覆盖,那么我们就看这两个状态是从哪里转移过来进行更新的。如果f[i][k]与f[k][j]这两个状态的转移会依赖于当前状态之后的状态,那么删除第一维度就是错误的,反之就是成立的。尝试推导
f[i][k]与f[k][j]从何转移更新:利用我们未删除维度时正确的状态转移方程进行推演我们知道:
f[k][i][k] = min(f[k-1][i][k], f[k-1][i][k] + f[k-1][k][k]),其中的f[k-1][k][k]就是一个自环的路径长度,由于算法的约束条件是没有负环,因此 f l o y d floyd f[k-1][k][k]一定大于零,故f[k][i][k]一定取前者,即f[k][i][k] = f[k-1][i][k]同理可知:
f[k][k][j] = f[k-1][k][j]基于上述推导我们可以知道,当前第
个决策局面中的 k k f[k][i][k]与f[k][k][j]是依赖于上一个决策局面的,也就是说这两个状态一定是早于当前状态 k − 1 k-1 f[i][j]被更新覆盖的,故f[i][k]与f[k][j]就是当前第个局面的最优子结构,证毕,可以进行维度的删除 k k 时间复杂度:
O ( n 3 ) O(n^3) 空间复杂度:
O ( n 2 ) O(n^2)
不优化空间
1 | |
优化空间
1 | |
【最短路】关闭分部的可行集合数目
https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/
标签:二进制枚举、最短路
题意:给定一个含有
个顶点的无向图,如何删点可以使得剩余的图中顶点两两可达且最大距离不超过 maxDistance?返回所有删点的方案数。 n n 思路:由于
的数据范围只有 n n ,我们可以直接枚举所有的删点方案。那么如何检查一个方案的合法性呢?直接使用最短路算法检查「所有顶点到每一个顶点」的最远距离即可。这里我们采用朴素 dijkstra 算法。 1 → 10 1 \to 10 时间复杂度:
- 其中枚举需要 O ( 2 n × n 3 ) O(2^n \times n^3) 、计算所有顶点到某个顶点的最远距离需要 O ( 2 n ) O(2^n) 、检查所有顶点需要 O ( n 2 ) O(n^2) O ( n ) O(n)
1 | |
1 | |
【思维/遍历】图的遍历
https://www.luogu.com.cn/problem/P3916
题意:给定一个有向图,求解每一个点可以到达的编号最大的点
思路:如果从正向考虑,很显然的一个暴力方法就是对于每一个点都跑一遍 dfs 或者 bfs 获取可达的最大点编号,时间复杂度
,如果想要在遍历的过程中同时更新其余的点,那只有起点到最大点之间的点可以被更新,可以通过递归时记录路径点进行,时间复杂度几乎不变。我们尝试反向考虑:反向建边。既然正向考虑时需要标记的点为最大点与起点的路径,那不如直接从最大值点开始遍历搜索,在将所有的边全部反向以后,从最大值点开始遍历图,这样就可以在线性时间复杂度内解决问题 O ( n 2 ) O(n^2) 时间复杂度:
O ( n + m ) O(n+m)
bfs 代码
1 | |
dfs 代码
1 | |
【遍历/并查集】孤立点数量
https://www.acwing.com/problem/content/5560/
题意:给定一个无向图,可能不连通,没有重边和自环。现在需要给图中的每一条无向边定向,要求所有的边定完向以后 0 入度的点尽可能的少,给出最少的 0 入度点的数量
思路:我们知道对于一棵树而言,n 个结点一共有 n-1 条边,也就可以贡献 n-1 个入度,因此至少有一个点的入度为 0。而如果不是一棵树,就会有至少 n 条边,也就至少可以贡献 n 个入度,那么 n 个结点就至少全都有入度了。显然的,一个图至少含有 n 条边时就一定有环。有了上述思路以后就可以发现,这道题本质上就是在判断连通分量是否含有环,如果有环,那么该连通分量定向边以后就不会产生 0 入度的顶点,反之,如果没有环,那么定向边以后最少产生 1 个 0 入度的点。
算法一:遍历图。我们采用 dfs 遍历的方式即可解决问题。一边遍历一边打标记,遇到已经打过标记的非父结点就表明当前连通分量有环。我们使用 C++ 实现
时间复杂度:
O ( n + m ) O(n+m) 算法二:并查集。由于没有重边,因此在判断每一个连通分量是否含有环时,可以直接通过该连通分量中点和边的数量关系得到结果。我们使用 Python 和 JavaScript 实现
时间复杂度:
O ( n ) O(n)
C++
1 | |
Python
1 | |
JavaScript
1 | |
【LCA】树的直径
https://www.acwing.com/problem/content/5563/
题意:给定一棵树,初始时含有 4 个结点分别为 1 到 4,其中 1 号为根结点,2 到 4 均为根结点的叶子结点。现在进行 Q 次操作,每次指定一个已经存在的结点向其插入两个新结点作为叶节点。现在需要在每次操作以后输出这棵树的直径。我们定义树的直径为:树中距离最远的两个点之间的距离。
思路一:暴力搜索。
我们将树重构为无向图,对于每一个状态的无向图,首先从任意一个已存在的结点 A 开始搜索到距离他最远的点 B,然后从 B 点出发搜索到离他最远的点 C,则 B 与 C 之间的距离就是当前状态的树的直径。由于每一个状态的树都要遍历两遍树,于是时间复杂度就是平方阶
时间复杂度:
O ( q n ) O(qn) 思路二:最近公共祖先 LCA。
从树的直径出发。我们知道,树的直径由直径的两个结点之间的距离决定,因此我们着眼于这两个结点
和 A A 展开。不妨设当前局面直径的两个结点已知为 B B 和 A A ,现在插入两个叶子结点 B B 和 L 1 L_1 。是否改变了树的直径大小取决于新插入的两个结点对于当前树的影响情况。如果 L 2 L_2 或 L 1 L_1 可以替代 L 2 L_2 或 A A ,则树的直径就会改变。很显然新插入的两个叶子结点对于直径的两个端点影响是同效果的,因此我们统称新插入的叶子结点为 B B 。 L L 什么时候树的直径会改变?对于
、 A A 和 B B 来说,直径是否改变取决于 L L 能否替代 L L 或 A A ,一共有六种情况。我们记 B B , dist ( A , L ) = d a \text{dist}(A,L)=da ,当前树的直径为 dist ( B , L ) = d b \text{dist}(B,L)=db ,六种情况如下: r e s res
,交换 max ( d a , d b ) ≤ res \text{max}(da, db) \le \text{res} 和 A A 得到 B B 种 2 2 ,交换 min ( d a , d b ) ≥ res \text{min}(da,db) \ge \text{res} 和 A A 得到 B B 种 2 2 ,交换 max ( d a , d b ) > r e s , min ( d a , d b ) < res \text{max}(da,db) >res,\text{min}(da,db) < \text{res} 和 A A 得到 B B 种 2 2 如图:我们只需要在其中的最大值严格超过当前树的直径
时更新直径对应的结点以及直径的长度即可 res \text{res}
如何快速计算树上任意两个点之间的距离?我们可以使用最近公共祖先 LCA 算法。则树上任意两点
之间的距离 x , y x,y 为: dist ( x , y ) \text{dist}(x,y)
dist ( x , y ) = dist ( x , r o o t ) + dist ( y , r o o t ) − 2 × dist ( lca ( x , y ) , r o o t ) \text{dist}(x,y) = \text{dist}(x,root) + \text{dist}(y,root) - 2 \times \text{dist}(\text{lca}(x,y),root) 时间复杂度:
O ( q log n ) O(q \log n)
暴力搜索代码
1 | |
LCA 代码
1 | |
整数问题。
【质数】Divide and Equalize
题意:给定
个数,问能否找到一个数 n n ,使得 n u m num n u m n = ∏ i = 1 n a i num^n = \prod_{i=1}^{n}a_i 原始思路:起初我的思路是二分,我们需要寻找一个数使得n个数相乘为原数组所有元素之积,那么我们预计算出所有数之积,并且在数组最大值和最小值之间进行二分,每次二分出来的数计算n次方进行笔比较即可。但是有一个很大的问题是,数据量是
,而数字最大为 1 0 4 10^4 ,最大之积为 1 0 6 10^6 吗?不是!最大之和才是,最大之积是 1 0 10 10^{10} 1 0 6 × 1 0 4 10^{6\times10^4} 最终思路:我们可以将选数看做多个水池匀水的过程。现在每一个水池的水高都不定,很显然我们一定可以一个值使得所有的水池的高度一致,即
。但是我们最终的数字是一个整数,显然不可以直接求和然后除以n,那么应该如何分配呢?我们知道水池之所以可以直接除以n,是因为水的最小分配单位是无穷小,可以随意分割;而对于整数而言,最小分配单位是什么呢?答案是质因子!为了通过分配最小单位使得最终的“水池高度一致”,我们需要让每一个“水池”获得的数值相同的质因子数量相同。于是我们只需要统计一下数组中所有数的质因子数量即可。如果对于每一种质因子的数量都可以均匀分配每一个数(即数量是n的整数倍),那么就一定可以找到这个数使得 ∑ i = 1 n a i n \frac{\sum_{i=1}^{n}a_i}{n} n u m n = ∏ i = 1 n a i num^n = \prod_{i=1}^{n}a_i
1 | |
【整除】Deja Vu
https://codeforces.com/contest/1891/problem/B
题意:给点序列 a 和 b,对于 b 中的每一个元素
,如果 a 中的元素 b i b_i 能够整除 a j a_j ,则将 2 b i 2^{b_i} 加上 a j a_j 。给出最后的 a 序列 2 b i − 1 2^{b_i - 1} 思路一:暴力枚举。
我们很容易就想到暴力的做法,即两层循环,第一层枚举 b 中的元素,第二层枚举 a 中的元素,如果 a 中的元素能够整除 2 的
次方,就将 a 中相应的元素加上一个值即可。但是时间复杂度肯定过不了,考虑优化。 b i b^i 时间复杂度:
O ( n m ) O(nm) 思路二:整除优化。
现在我们假设a中有一个数
是 a j a_j 的整数倍(其中 2 b i 2^{b_i} 是b序列中第一个枚举到的能够让 b i b_i 整除的数),那么就有 a i a_i ,那么 a j = k 2 b i ( k = 1 , 2 , . . . , ) a_j = k2^{b_i}(k=1,2,...,) 就要加上 a j a_j ,于是 2 b i − 1 2^{b_i-1} 就变为了 a j a_j 。此后 k 2 b i + 2 b i − 1 = ( 2 k + 1 ) 2 b i − 1 k2^{b_i}+2^{b_i-1}=(2k+1)2^{b_i-1} 就一定是 a j a_j 的倍数。因此我们需要做的就是首先找到b序列中第一个数x,能够在a中找到数是 2 t ( t ∈ [ 1 , b i − 1 ] ) 2^t(t\in \left[ 1,b_i-1 \right]) 的整数倍。这一步可以这样进行:对于 a中的每一个数,我们进行30次循环统计当前数是否是 2 x 2^x 的倍数,如果是就用哈希表记录当前的 2 i 2^i 。最后我们在遍历寻找 x 时,只需要查看当前的 x 是否被哈希过即可。接着我们统计b序列中从x开始的严格降序序列c(由题意知,次序列的数量一定 i i 30,因为b序列中数值的值域为 ≤ \le )。最后我们再按照原来的思路,双重循环 a 序列和 c 序列即可。 [ 1 30 ] [1~30] 时间复杂度:
O ( 30 n ) O(30n)
1 | |
【组合数学】序列数量
https://www.acwing.com/problem/content/5571/
题意:给定
个苹果,将其分给 i ( i = 1 , 2 , ⋯ , n ) i(i=1,2,\cdots,n) 个人,问一共有多少种分配方案,给出结果对 m m 取模的结果 1 0 6 + 3 10^6+3 思路:整数分配问题。我们采用隔板法,隔板法相关例题见这篇博客:https://www.acwing.com/solution/content/241669/。下面开始讲解
利用隔板法推导结果。首先我们考虑当前局面,即只有 i 个苹果的情况下的方案数。于是题目就是 i 个苹果分给 m 个人,允许分到 0 个。于是借鉴上述链接中“少分型”的思路,先借 m 个苹果,那么此时局面中就有 i+m 个苹果,现在就等价于将 i+m 个苹果分给 m 个人,每人至少分得 1 个苹果。(分完以后每个人都还回去就行了),此时的隔板操作就是”标准型”,即 i+m 个苹果产生 i+m-1 个间隔,在其中插 m-1 块板,从而将划分出来的 m 个部分分给 m 个人。此时的划分方案就是
,那么对于所有的 i,结果就是 C i + m − 1 m − 1 C_{i+m-1}^{m-1}
∑ i = 1 n C i + m − 1 m − 1 = C m m − 1 + C m + 1 m − 1 + ⋯ + C n + m − 1 m − 1 = C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n = ( − C m 0 + C m 0 ) + C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n = − C m 0 + ( C m 0 + C m 1 + C m + 1 2 + ⋯ + C n + m − 1 n ) = − 1 + ( C m + 1 1 + C m + 1 2 + ⋯ + C n + m − 1 n ) = − 1 + ( C m + 2 2 + ⋯ + C n + m − 1 n ) = − 1 + C n + m n \begin{aligned}\sum_{i=1}^n C_{i+m-1}^{m-1} &= C_{m}^{m-1} + C_{m+1}^{m-1} + \cdots + C_{n+m-1}^{m-1} \\&= C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\&= (-C_{m}^{0}+C_{m}^{0})+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\&= -C_{m}^{0}+(C_{m}^{0}+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+(C_{m+1}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+(C_{m+2}^{2} + \cdots + C_{n+m-1}^{n}) \\&= -1+C_{n+m}^n\end{aligned} 利用乘法逆元计算组合数。结果已经知道了,现在如何计算上述表达式呢?由于
超过了常规递推的组合数计算方法内存空间,因此我们采用乘法逆元的思路计算。值得一提的是,本题在计算某个数关于 n × m n\times m 1e6+3的乘法逆元时,不需要判断两者是否互质,因为1e6+3是一个质数,并且数据范围中的数均小于1e6+3,因此两数一定互质,可以直接使用费马小定理计算乘法逆元时间复杂度:
O ( n log 1 e 6 ) O(n\log 1e6)
1 | |
大胆猜测,小心求证(不会证也没事,做下一题吧)。证明方法总结了以下几种
- 反证法:假设取一种方案比贪心方案更好,得出相反的结论
- 边界法:从边界开始考虑,因为满足边界条件更加容易枚举,从而进行后续的贪心
- 直觉法:遵循社会法则()
1. green_gold_dog, array and permutation
https://codeforces.com/contest/1867/problem/A
题意:给定n个数a[i],其中可能有重复数,请构造一个n个数的排列b[i],使得c[i]=a[i]-b[i]中,c[i]的不同数字的个数最多
思路:思路比较好想,就是最大的数匹配最小的数,次大的数匹配次小的数,以此类推。起初我想通过将原数列的拷贝数列降序排序后,创建一个哈希表来记录每一个数的排位,最终通过原数列的数作为键,通过哈希表直接输出排位,但是问题是原数列中的数可能会有重复的,那么在哈希的时候如果有重复的数,那么后来再次出现的数就会顶替掉原来的数的排位,故错误。
正确思路:为了保证原数列中每个数的唯一性,我们可以给原数列每一个数赋一个下标,排序后以下标进行唯一的一一对应的索引。那么就是:首先赋下标,接着以第一关键词进行排序,然后最大的数(其实是下标)匹配最小的结果以此类推
模拟一个样例:
5
8 7 4 5 5 9最终的答案应该是
2 3 6 4 5 1首先对每一个数赋予一个下标作为为唯一性索引
8 7 4 5 5 9
1 2 3 4 5 6(替身)接着将上述数列按照第一关键词进行排序
9 8 7 5 5 4
6 1 2 4 5 3(替身)对每一个数进行赋值匹配
9 8 7 5 5 4
6 1 2 4 5 3(替身)
1 2 3 4 5 6(想要输出的结果)按照替身进行排序
8 7 4 5 5 9
1 2 3 4 5 6(替身)(排序后)
2 3 6 4 5 1(想要输出的结果)
1 | |
2. Good Kid
https://codeforces.com/contest/1873/problem/B
题意:对于一个数列,现在可以选择其中的一个数使其+1,问如何选择这个数,可以使得修改后的数列中的所有数之积的值最大
思路:其实就是选择n-1个数的乘积值加一倍,关键在于选哪一个n-1个数的乘积值,逆向思维就是对于n个数,去掉那个最小值,那么剩下来的n-1个数之积就会最大了,于是就是选择最小的数+1,最终数列之积就是答案了。
1 | |
3. 1D Eraser
https://codeforces.com/contest/1873/problem/D
题意:给定一个只有B和W两种字符的字符串,现在有一种操作可以将一个指定大小的区间(大小为k)中所有的字符全部变为W,问对于这个字符串,至少需要几次上述操作才可以将字符串全部变为W字符
思路:我们直接遍历一边字符串即可,在遍历到B字符的时候,指针向后移动k位,如果是W字符,指针向后移动1位即可,最终统计一下遇到B字符的次数即可。
1 | |
4. ABBC or BACB
https://codeforces.com/contest/1873/problem/G
题意:现在有一个只有A和B两种字符的字符串,有如下两种操作:第一种,可以将AB转化为BC,第二种,可以将BA转化为CB。问最多可以执行上述操作几次
思路:其实一开始想到了之前做过的翻转数字为-1,最后的逻辑是将数字向左右移动,于是这道题就有了突破口了。上述两种操作就可以看做将A和B两种字符交换位置,并且B保持不变,A变为另一种字符C。由于C是无法执行上述操作得到,因此就可以理解为B走过的路就不可以再走了,那么就是说对于一个字符串,最终都会变成B走过的路C。并且只要有B,那么一个方向上所有的A都会被利用转化为C(直到遇到下一个B停止),那么我们就可以将B看做一个独立的个体,他可以选择一个方向上的所有的A并且执行操作将该方向的A全部转化为C,那么在左和右的抉择中,就是要选择A数量最多的方向进行操作,但是如果B的足够多,那就不需要考虑哪个方向了,所有的A都可以获得一次操作机会。现在就转向考虑B需要多少呢,
答案是两种:如果B的数量小于A“块”的数量,其实就是有一块A无法被转化,那么为了让被转化的A数量尽可能的多,就选择A块数量最少的那一块不被转化。如果B的数量>=A块的数量,那么可以保证所有的A都可以被转化为C块,从而最终的答案就是A字符的数量
1 | |
5. Smilo and Monsters
https://codeforces.com/contest/1891/problem/C
题意:给定一个序列,其中每一个元素代表一个怪物群中的怪物的数量。现在有两种操作:
- 选择一个怪物群,杀死其中的一只怪物。同时累加值
x + = 1 x+=1 - 选择一个怪物群,通过之前积累的累加值,一次性杀死当前怪物群中的
只怪物,同时累加值 x x 归零 x x 现在询问杀死所有怪物的最小操作次数
思路:一开始我是分奇偶进行判断的,但是那只是局部最优解,全局最优解的计算需要我们“纵观全局”。
我们可以先做一个假设:假设当前只有一个怪物群,为了最小化操作次数,最优解肯定是先杀死一半的怪物(假设数量为n,则获得累计值x=n),然后无论剩余n个还是n+1个,我们都使用累计值x一次性杀死n个怪物。
现在我们回到原题,有很多个怪物群,易证,最终的最优解也一点是最大化利用操作2,和特殊情况类似,能够利用的一次性杀死的次数就是怪物总数的一半。区别在于:此时不止一个怪物群。那么我们就要考虑累加值如何使用。很容易想到先将怪物群按照数量大小进行排序,关键就在于将累加值从小到大进行使用还是从大到小进行使用。可以发现,对于一个确定的累加值,由于操作2的次数也会算在答案中。那么如果从最小的怪物群开始使用,就会导致操作2的次数变多。因此我们需要从最大值开始进行操作2。
那么最终的答案就是:
- 首先根据怪物数量的总和计算出最终的累加值s(s=sum/2)
- 接着我们将怪物群按照数量进行升序排序
- 然后我们从怪物数量最大的开始进行操作2,即一次性杀死当前怪物群,没进行一次,答案数量+1
- 最后将答案累加上无法一次性杀死的怪物群中怪物的总数
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
6. 通关
https://www.lanqiao.cn/problems/5889/learning/?contest_id=145
声明:谨以此题记录我的第一道正式图论题(存图技巧抛弃了y总的纯数组,转而使用动态数组
vector进行建图)e.g.
2
3
4
5
6struct Node {
int id; // 当前结点的编号
int a; // 属性1
int b; // 属性2
};
vector<Node> G[N];题意:给定一棵树,每个结点代表一个关卡,每个关卡拥有两个属性:通关奖励值
val和可通关的最低价值cost。现在从根节点开始尝试通关,每一个结点下面的关卡必须要当前结点通过了之后才能继续闯关。问应该如何选择通关规划使得通过的关卡数最多?思路:一开始想到的是直接莽bfs,对每一层结点按照cost升序排序进行闯关,然后wa麻了。最后一看正解原来是还不够贪。正确的闯关思路应该是始终选择当前可以闯过的cost最小的关卡,而非限定在了一层上。因此我们最终的闯关顺序是:对于所有解锁的关卡,选择cost最小的关卡进行通关,如果连cost最小的关卡都无法通过就直接结束闯关。那么我们应该如何进行代码的编写呢?分析可得,解锁的关卡都是当前可通过的关卡的所有子结点,而快速获得当前cost最小值的操作可以通过一个堆来维护。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
7. 串门
https://www.lanqiao.cn/problems/5890/learning/?contest_id=145
题意:给定一棵无向树,边权为正。现在询问在访问到每一个结点的情况下最小化行走的路径长度
思路:首先我们不管路径长度的长短,我们直接开始串门。可以发现,我们一点会有访问的起点和终点,那么在起点到终点的这条路上,可能会有很多个分叉,对于每一个分叉,我们都需要进入再返回来确保分叉中的结点也被访问到,那么最终的路径长度就是总路径长度的2倍 - 起点到终点的距离,知道了这个性质后。我们可以发现,路径的总长度是一个定值,我们只有最大化起点到终点距离才能确保行走路径长度的最小值。那么问题就转化为了求解一棵树中,最长路径长度的问题。即求解树的直径的问题。
树的直径:首先我们反向考虑,假设知道了直径的一个端点,那么树的直径长度就是这棵树以当前结点为根的深度。那么我们就需要先确定一个直径的端点。不难发现,对于树中的任意一个结点,距离它最远的一个(可能是两个)结点一定是树的直径的端点。那么问题就迎刃而解了。
为了降低代码量,我们可以设置一个dist数组来记录当前结点到根的距离。
- 在确定直径端点的时候,选择任意一个结点为根节点,然后维护dist数组,最终dist[i~n]中的最大值对应的下标maxi就是直径的一个端点。
- 接着在计算直径长度的时候,以maxi为树根,再来一次上述的维护dist数组的过程,最终dist[1~n]中的最大值就是树的直径的长度
时间复杂度:
O ( n ) O(n)
1 | |
8. Codeforces rating
https://vijos.org/d/nnu_contest/p/1532
题意:现在已知一个初始值R,现在给定了n个P值,选择其中的合适的值,使得最终的
最大 R ′ = 3 / 4 R + 1 / 4 P R'=3/4 R + 1/4 P 思路:首先一点就是我们一定要选择P比当前R大的值,接下来就是选择合适的P使得最终迭代出来的R’最大。首先我们知道,对于筛选出来的比当前R大的P集合,任意选择其中的一个P,都会让R增大,但是不管增加多少都是不会超过选择的P。那么显然,如果筛选出来的P集合是一个递增序列,那么就可以让R不断的增加。但是这一定是最大的吗?我们不妨反证一下,现在我们有两个P,分别为x,y,其中
。 x < y x<y 那么按照上述思路,首先就是
R ′ = 3 4 R + 1 4 x ( R ′ < x ) R'=\frac{3}{4}R+\frac{1}{4}x(R'<x) 接着就是
R 1 ′ ′ = 3 4 R ′ + 1 4 y ( R 1 ′ ′ < y ) = 9 16 R + 3 16 x + 1 4 y R''_1=\frac{3}{4}R'+\frac{1}{4}y(R''_1<y)=\frac{9}{16}R+\frac{3}{16}x+\frac{1}{4}y 反之,首先选择一个较大的P=y,再选择一个较小的P=x,即首先就是
R ′ = 3 4 R + 1 4 y ( R ′ < y ) R'=\frac{3}{4}R+\frac{1}{4}y(R'<y) 此时我们还不一点可以继续选择x,因为此时的R’可能已经超过了x的值,那么我们按照最优的情况计算,可以选择x,那么就是
R 2 ′ ′ = 3 4 R ′ + 1 4 x ( R 2 ′ ′ < x ) = 9 16 R + 3 16 y + 1 4 x R''_2=\frac{3}{4}R'+\frac{1}{4}x(R''_2<x)=\frac{9}{16}R+\frac{3}{16}y+\frac{1}{4}x 可以发现
R 2 ′ ′ − R 1 ′ ′ = 1 16 ( x − y ) < 0 R''_2-R''_1=\frac{1}{16}(x-y)<0 即会使得最终的答案变小。因此最优的策略就是按照增序进行叠加计算
==注意点:==
四舍五入的语句
cout << (int)(res + 0.5) << "\n";
1 | |
9. 货运公司
https://www.acwing.com/problem/content/5380/
题意:给定
个运货订单,每个订单需要运送一定量的货物,同时给予一定量的报酬。现在有 n n 个卡车进行运送,每个卡车有运送容量。需要合理规划卡车的装配,使得最终获得的总报酬最大。有以下约束条件: k k
- 每一个订单只能用一辆货车运送
- 每一辆货车只能运送不超过最大容量的货物
- 每一辆货车只能运送一次
- 每一辆货车在装得下的情况下只能装运一个订单
思路:一开始尝试采用 01 背包的思路,但是题目中货物是否可以被运送是取决于卡车的装载的。思考无果后考虑贪心。考虑一般情况
为了让总收益最大,很显然报酬越多,就越优先选择该订单
在报酬一致时,货物量越少,就越优先选择该订单
按照上述规则对订单排序后,我们需要安排合理的货车进行运输。我们优先将运输量小的货车安排给合适的订单。因为运输量大的货车既可以满足当前订单,同样也满足后续的订单,那么为了最大化增加利润,就需要在运输量小的货车满足当前订单时,保留运输量大的货车用于后续的订单。我们可以画一个图进一步理解为什么这么安排货车进行运输:
 图例:我们按照上述红笔的需要进行货车的选择进行运输
图例:我们按照上述红笔的需要进行货车的选择进行运输如果红色序号顺序变掉了,则就不能将上述图例中的 6 个订单全部运输了
时间复杂度
O ( n k ) O(nk)
1 | |
10. 部分背包问题
https://www.luogu.com.cn/problem/P2240
- 题意:给定一组物品,每一个物品有一定的重量与价值,现在给定一个背包总承重,需要从中选择合适的物品进行装载,使得最终装载的物品的总价值最大。现在规定每一个物品可以进行随意分割,按照单位重量计算价值
- 思路:考虑一般情况。很显然,如果不说可以随意分割,那就是一个 01 背包,既然说了可以随意分割,那就直接贪心选择即可,按照单位重量的价值降序进行选择
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
11. 排队接水
https://www.luogu.com.cn/problem/P1223
题意:贪心经典,排队接水,每一个人都有一个打水时间,现在询问如何排队能够使得平均等待时间最短
思路:考虑一般情况。注意问的是平均等待时间,如果是打完水总花费时间那就是一个定值,即所有人打水的时间总和。现在为了让平均等待时间最短,我们的第一反应应该是,在人多的时候让打水时间短的先打,人少的时候让打水时间长的再打,那么很显然就是按照打水时间的升序进行排队。为了证明这个结论,我们采用数学归纳法,如下,对于一个排队序列来说,我们将其中的两个顺序进行颠倒,计算结果得到让打水时间短的排在前面更优,进而推广到一般情况,于是按照打水时间升序进行打水的策略是最优的。证毕
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
12. 线段覆盖
https://www.luogu.com.cn/problem/P1803
- 题意:给定一个数轴和数轴上的 n 个线段,现在需要从中选出尽可能多的 k 个线段,使得线段之间两两不相交,问 k 最大是多少
- 思路:绞尽脑汁想着各种情况进行分类讨论,什么包含、相交、相离,但是都忽视了最重要的一点,那就是一开始应该选择线段。即考虑边界,对于最左侧我们应该选择哪一条线段呢?答案是最左侧的右端点最靠左的那一条线段,这样子后续的线段才能有更多的摆放空间
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
13. 小A的糖果
https://www.luogu.com.cn/problem/P3817
- 题意:给定一个序列,现在每次可以选择序列中的某个数进行减一操作,问最少需要减多少可以使得序列中相邻两个元素之和不超过规定的数值 x
- 思路:同 T12 的思路展开,考虑边界,我们直接从任意的一个边界开始思考,假设从左边界开始考虑。为了让左边界满足,那么 a[1] 与 a[2] 之和就需要满足条件,为了后续可以尽可能少的进行减一操作,很显然我们最好从两个数的右边的数开始下手,于是贪心的结果就有了
- 时间复杂度:
O ( n ) O(n)
1 | |
15. 陶陶摘苹果(升级版)
https://www.luogu.com.cn/problem/P1478
- 题意:现在有 n 个苹果,含有高度和消耗体力值两个属性,现在你有一个最大高度以及总体力值,每次只能摘高度值不超过最大高度的苹果且会消耗相应的体力值。问最多可以摘多少个苹果
- 思路:既然是想要摘的苹果尽可能多,那么高度都是浮云,体力值才是关键。为了摘得尽可能多的苹果,自然是消耗体力越少越优先摘。于是按照消耗体力值升序排序后,扫描一遍即可计数
- 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
16. [NOIP2018 提高组] 铺设道路
https://www.luogu.com.cn/problem/P5019
题意:给定一个序列,每次可以选择一个连续的区间使得其中的所有数 -1,前提是区间中的数都要 > 1,问最少选择几次区间可以将所有的数全部都减到 0
思路:很显然的一个贪心思路就是,对于一个数,左右两侧均呈现递减的趋势,那么这个区间的选择数就是这个最大的数的值。但是这不符合代码逻辑,我们尝试从端点开始考虑。为了更好的理解,我们从递推的角度进行推演。假设填平前 i 个数花费的选择次数为 f[i],那么对于第一个数 a[1],我们一定需要花费 a[1] 次选择来将其减到零,于是 f[1] = a[1];对于后续的数而言,可以发现
- 如果 a[i] > a[i-1],那么之前的选择没有完全波及当前的数,还需要一定的次数来将其减到零,于是
f[i] = f[i-1] + a[i] - a[i-1]- 如果 a[i]
a[i-1],那么当前的数值一定会被之前的选择“波及”而直接减到零,于是 ≤ \le f[i] = f[i-1]从递推的角度理解之后我们直接滚动一遍数组记录増势即可
时间复杂度:
O ( n ) O(n)
1 | |
17. [USACO1.3] 混合牛奶 Mixing Milk
https://www.luogu.com.cn/problem/P1208
- 题意:现在需要收集 need 容量的牛奶,同时有 n 个农户提供奶源,每一个商户的奶源有一定的数量与单价,问如何采购可以在满足需求 need 的情况下成本最低化
- 思路:很显然单价越低越优先采购
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
18. [NOIP2007 普及组] 纪念品分组
https://www.luogu.com.cn/problem/P1094
- 题意:给定 n 个数,问如何分组可以使得在每一组之和不超过定值 lim 且每一组最多两个数的情况下,分得的组数最少
- 思路:对序列没有要求,显然直接排序然后从一端开始考虑。首先有一个概念就是,为了尽可能的减少分得的组数,那么一定想要每一组分完后距离 lim 的差距越小越好。我们将 n 个数降序排序后,从最大值开始考虑,对于当前的数,为了找到一个数与当前数之和尽可能接近 lim,从贪心的角度来说一定是从当前数之后开始寻找那个配对的数从而使得两数之和与 lim 的差距最小,那么时间复杂度就是
。但是由于题目说了最多只有两个数,我们不妨换一种寻找配对数的策略,可以从原始的寻找方法得到启发,可以发现,原始的寻找配对数的方法中,如果找到的那个配对数可以与当前数之和不超过 lim 且之和尽可能的大,那么这个寻找到的配对数也一定可以和当前数的下一个数进行配对。由于我们一组只能有两个数,因此我们不用考虑两数组合之后比 lim 小的数尽可能的小,只需要考虑两个数能否组合即可,因此我们直接双指针进行寻找配对数操作即可 O ( n 2 ) O(n^2) - 时间复杂度:
O ( n ) O(n)
1 | |
19. 跳跳!
https://www.luogu.com.cn/problem/P4995
题意:给定 n 个数,每一个数代表一个高度,现在有一只青蛙从地面(高度为 0)开始起跳,每一个数字只能被跳上去一次。问如何设定跳数顺序 h[],可以使得下式尽可能的大
∑ i = 1 n ( h i − h i − 1 ) 2 \sum_{i=1}^n (h_i-h_{i-1})^2 思路:题目意思其实就是让每一次跳跃的两个高度之差尽可能的大。那么一个贪心的思路就是从地面跳到最高,再从最高跳到次低,接着从次低跳到次高,以此类推得到的结果就是最优解,为了证明我们可以用数学归纳法,假设当前只有两个高度可以选择,那么肯定是先跳高的再跳低的;假设当前有三个高度可以选择,那么可以证明先从地面跳到最高处,再跳到最低处,最后跳到第二高的方法得到的值最大
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
20. 安排时间
https://www.acwing.com/problem/content/5466/
- 题意:给定 n 个时间段处理餐厅事务,m 个用餐预定信息,含有三个信息分别为订单发起时间,订单需要准备的时间,客人来用餐时间。问如何安排每一个时间段,可以让所有的用户得到正常的服务。如果不能全部满足则输出 -1
- 思路:玄学贪心,先到的用户先做它的菜
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
21. [NOIP2004 提高组] 合并果子
https://www.luogu.com.cn/problem/P1090
- 题意:给定 n 个数,现在需要将其两两合并为最终的一个数,每次合并的代价是两个数之和,问如何对这些数进行合并可以使得总代价最小
- 思路:很显然一共需要合并 n-1 次。那么我们从三个物品开始考虑,然后使用数学归纳法推导到 n 个数。对于三个物品,很显然先将两个物品进行合并,再将这个结果与最大的数进行合并方案时最优的。那么推广到 n 个数,我们只需要每次合并当前局面中最小的两个数即可
- 时间复杂度:
O ( n log n ) O(n \log n)
1 | |
22. 删数问题
https://www.luogu.com.cn/problem/P1106
- 题意:给定一个数字字符串长度为 n,现在需要选择其中的 m 位数,使得这 m 位组成的数最小是多少 (m=n-k)
- 思路:我们从一端考虑问题。为了组成的数尽可能的小,我们希望从首位开始就尽可能的小,同时如果有重复的数字,就选择最左侧的,剩余的数字留给后续的位数继续选择。有一个需要注意的点就是选择每一位的数字时,范围的约束,我们假设需要从 10 位的数字串中选择 3 位,那么我们第一次选择时需要在 0-7位中选择一位,第二次选择在 上次选择的下一个位置到第8位中选择一位,以此类推进行贪心选择
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
23. 截断数组
https://www.acwing.com/problem/content/5483/
题意:定义平衡数组为奇偶数数量相同的数组,现在给定一个平衡数组,和一个总成本数,最多可以将原数组截成多少截子平衡数组,且截断代价总和不超过总成本,截断代价计算公式为
∣ a i − a i + 1 ∣ |a_i-a_{i+1}| 思路:我们直接枚举所有的可以被截断的位置,统计所有的代价值,然后根据成本总数按降序枚举代价值即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
24. 修改后的最大二进制字符串
https://leetcode.cn/problems/maximum-binary-string-after-change/description/
题意:给定一个仅由01组成的字符串,现在可以执行下面两种操作任意次,使得最终的字符串对应的十进制数值最大,给出最终的字符串
00 → 10 00 \to 10 10 → 01 10 \to 01 思路:
- 有点像之前做的翻转转化为平移的问题,事实确实如此。首先需要确定一点就是:如果字符串起始有连续的1,则保留,因为两种操作都是针对0的。接着就是对从第一个0开始的尾串处理的思路
- 对于尾串而言,我们自然希望1越多、越靠前越好,但是第二种操作只能将1向后移,第一种操作又必须要连续的两个0,因此我们就产生了这样的贪心思路:将所有的1通过操作二移动到串尾,接着对尾串的开头连续的0串执行第二种操作,这样就可以得到最大数值的二进制串
时间复杂度:
O ( n ) O(n)
1 | |
25. 子序列最大优雅度
https://leetcode.cn/problems/maximum-elegance-of-a-k-length-subsequence/
标签:反悔贪心
题意:给定长度为 n 的物品序列,现在需要从中寻找一个长度为 k 的子序列使得子序列的总价值最大,给出最终的最大价值。一个序列的价值定义为每个物品的 本身价值之和 + 物品种类数的平方
思路:我们采用反悔贪心的思路。首先按照物品本身价值进行降序排序并选择前 k 个物品作为集合 S,然后按顺序枚举剩下的物品进行替换决策。我们记每个物品有一个「本身价值」,集合 S 有一个「种类价值」。那么就会遇到下面两种情况:
- 第 i 个物品对应的种类存在集合 S 中。此时该物品「一定不选」,因为无论当前物品替代集合中的 S 哪一个物品,本身价值的贡献会下降、种类价值的贡献保持不变。
- 第 i 个物品对应的种类不在集合 S 中。此时该物品一定选择吗?不一定。有两种情况:
- 集合 S 没有重复种类的物品。此时该物品「一定不选」,同样的,无论当前物品替代集合中的 S 哪一个物品,本身价值的贡献会下降、种类价值的贡献保持不变。
- 集合 S 存在重复种类的物品。此时该物品「一定选」,因为一定可以提升种类价值的贡献,至于减去本身价值的损失后是否使得总贡献增加,并不具备可能的性质,只能每次替换物品时更新全局答案进行记录。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
1 | |
【按位贪心/分类讨论】
https://www.acwing.com/problem/content/1000/
题意:给定
个运算数和对应的 n n 个操作,仅有 n n &, |, ^三种。现在需要选择一个数使得 n u m ∈ [ 0 , m ] num \in [0,m] 经过这 n u m num 个二元运算后得到的结果 n n 最大。给出最终的 r e s res 。 r e s res 思路:首先不难发现这些运算操作在二进制位上是相互独立的,没有进位或结尾的情况,因此我们可以「按二进制位」单独考虑。由于运算数和
均 m m ,因此我们枚举 ≤ 1 0 9 \le 10^9 对应的二进制位。接下来我们单独考虑第 [ 0 , 30 ] [0,30] 位的情况,显然的 i i 的第 n u m num 位可以取 i i 也可以取 1 1 ,对应的 0 0 的第 r e s res 位可以取 i i 也可以取 1 1 。有以下 0 0 种运算情况: 2 2 2^2
$\text{num 的第 i 位填 1 res 第 i 位的情况}$ → \to $\text{num 的第 i 位填 0 res 第 i 位的情况}$ → \to 选择方案 情况一 1 → 0 1 \to 0 0 → 0 0 \to 0 num 填 0,res 填 0 情况二 1 → 0 1 \to 0 0 → 1 0 \to 1 num 填 0,res 填 1 情况三 1 → 1 1 \to 1 0 → 0 0 \to 0 待定 情况四 1 → 1 1 \to 1 0 → 1 0 \to 1 num 填 0,res 填 1 选择方案时我们需要考虑两个约束,
不能超过 n u m num , m m 尽可能大,因此有了上述表格第四列的贪心选择结果。之所以情况三待定是因为其对两种约束的相互矛盾的,并且其余情况没有增加 r e s res ,即对 n u m num 上限的约束仅存在于情况三。假设有 n u m num 位是上述情况三,那么显然的其余位枚举顺序是随意的,因为答案是固定的。对于 k k 个情况三,从贪心的角度考虑,我们希望 k k 尽可能大,那么就有「高位能出 r e s res 就出 1 1 」的结论。因此我们需要从高位到低位逆序枚举这 1 1 个情况三,由于其他位枚举顺序随意,因此总体就是从高位到低位枚举。 k k 时间复杂度:
O ( n log m ) O(n \log m)
1 | |
【二维/数学】Minimum Manhattan Distance
https://codeforces.com/gym/104639/problem/J
题意:给定两个圆的直径的两个点坐标,其中约束条件是两个圆一定是处在相离的两个角上。问如何在C2圆上或圆内找到一点p,使得点p到C1圆的所有点的曼哈顿距离的期望值最小
思路:
看似需要积分,其实我们可以发现,对于点p到C1中某个点q1的曼哈顿距离,我们一定可以找到q1关于C1对称的点q2,那么点p到q1和q2的曼哈顿距离之和就是点p到C1的曼哈顿距离的两倍(证明就是中线定理)那么期望的最小值就是点p到C1的曼哈顿距离的最小值。目标转化后,我们开始思考如何计算此目标的最小值,思路如下图
注意点:
- double的读取速度很慢,可以用
intorlong long读入,后续强制类型转换(显示 or 和浮点数计算)- 注意输出答案的精度控制
cout << fixed << setprecision(10) << res << "\n";
1 | |
【枚举】三角形
https://www.acwing.com/problem/content/5383/
题意:给定两个直角三角形的两条直角边的长度 a, b,问能不能在坐标轴上找到三个整数点使得三点满足该直角三角形且三遍均不与坐标轴垂直
思路:首先确定两个直角边的顶点为原点 (0, 0),接着根据对称性直接在第一象限中按照边长枚举其中一个顶点 A,对于每一个枚举到的顶点 A,按照斜率枚举最后一个顶点 B,如果满足长度以及不平行于坐标轴的条件就是合法的点。如果全部枚举完都没有找到就是没有合法组合,直接输出 NO 即可。
时间复杂度:
O ( a 2 b ) O(a^2b)
1 | |
【凸包】奶牛过马路
https://www.acwing.com/problem/content/5572/
题意:给定一个二维坐标系,现在有两个东西可以进行平移。
- 一个是起始位于
的奶牛,可以沿着 ( 0 , 0 ) (0,0) 轴以 y y 的速度正向或负向移动 [ 0 , u ] [0,u] - 一个是起始位于第一象限的凸包形状的车辆,可以向
轴负半轴以恒定的速度 x x 移动 v v 在给定凸包的
个顶点的情况下,以及不允许奶牛被车辆撞到的情况下,奶牛前进到 n n 的最短时间 ( 0 , w ) (0,w) 思路:由于是凸包,因此每一个顶点同时满足的性质,就可以代表整个凸包满足的性质。那么对于奶牛和凸包,就一共有三个局面:
- 奶牛速度足够快。可以使得对于任意一个顶点
在到达 y 轴时,都小于此时奶牛的 y 值,用时间来表示就是 ( x , y ) (x,y) ,即 y u ≤ x v \frac{y}{u} \le \frac{x}{v} ,表示凸包上所有的顶点都在直线 y ≤ u v x y \le \frac{u}{v}x 的下方 y = u v y=\frac{u}{v} - 凸包速度足够快。可以使得对于任意一个顶点
在到达 y 轴时,都大于此时奶牛的 y 值,用时间来表示就是 ( x , y ) (x,y) ,即 y u ≥ x v \frac{y}{u} \ge \frac{x}{v} ,表示凸包上所有的顶点都在直线 y ≥ u v x y \ge \frac{u}{v}x 的上方 y = u v y=\frac{u}{v} - 上述两种都不满足,即直线
与凸包相交。此时奶牛就不能一直全速(u)前进到终点了,需要进行一定的减速 or 返回操作。有一个显然的结论就是,对于减速 or 返回的操作,都可以等价于后退一段距离后再全速(u)前进,因此对于需要减速 or 返回的操作,我们只需要计算出当前状态下应该后退的距离即可。再简洁的,我们就是需要平移直线 y = u v y=\frac{u}{v} ,显然只能向下平移而非向上平移,因此其实就是计算出直线 y = u v y=\frac{u}{v} 的截距 y = u v + b y=\frac{u}{v}+b 使得最终的直线 b b 满足第二种条件即可。那么如何计算这个 b 呢?很显然我们可以遍历每一个顶点取满足所有顶点都在直线 y = u v + b y=\frac{u}{v}+b 上方的最大截距 b 即可。 y = u v + b y=\frac{u}{v}+b 注意点:
- 浮点数比较注意精度误差,尽可能将除法转化为乘法
- 在比较相等时可以引入一个无穷小量
ϵ = 1 0 − 7 \epsilon=10^{-7} - 注意答案输出精度要求,
就需要我们出至少 1 0 − 6 10^{-6} 位小数 7 7 时间复杂度:
O ( n ) O(n)
C++
1 | |
Py
1 | |
优雅的解法,少不了优雅的板子。目前仅编写 C++ 和 Python 语言对应的板子。前者用于备赛 Xcpc,后者用于备赛蓝桥杯。
基础算法
高精度
1 | |
二分
闭区间寻找左边界:
1 | |
闭区间寻找右边界:
1 | |
哈希
使用 std::unordered_map 时可能会因为哈希冲突导致查询、插入操作降低到 std::map 进行替代,或者自定义一个哈希函数。
1 | |
数据结构
并查集
1 | |
1 | |
树状数组
1 | |
1 | |
SortedList
有序列表,改编于 from sortedcontainers import SortedList,共有以下内容:
- 公开方法:全部都是
O ( log n ) O(\log n) add(value): 添加一个值到有序列表discard(value): 删除列表中的值(如果存在)remove(value): 删除列表中的值(必须存在)pop(index=-1): 删除并返回指定索引处的值bisect_left(value): 返回插入值的最左索引bisect_right(value): 返回插入值的最右索引count(value): 计算值在列表中的出现次数
- 魔法方法
__init__():初始化传入一个可迭代对象__len__(): 返回列表的长度__getitem__(index): 获取指定索引处的值 -O ( log n ) O(\log n) __delitem__(index): 删除指定索引处的值 -O ( log n ) O(\log n) __contains__(value): 检查值是否在列表中 -O ( log n ) O(\log n) __iter__(): 返回列表的迭代器__reversed__(): 返回列表的反向迭代器__repr__(): 返回列表的字符串表示形式
1 | |
引自:https://www.acwing.com/activity/content/code/content/8475415/
官方:https://github.com/grantjenks/python-sortedcontainers/blob/master/src/sortedcontainers/sortedlist.py
数学
模运算
1 | |
质数筛
1 | |
乘法逆元
之所以需要知道一个数
的乘法逆元,是为了将除法在模 a a 的前提下转化为乘法,从而简化运算。推导 p p 的乘法逆元的逻辑如下: a a
对于任意
的整数倍 a a ,一定有下式成立:其中的 t t 就是整数 x x 的乘法逆元,记作 a a a − 1 a^{-1}
t a ≡ t × x ( m o d p ) 1 a ≡ 1 × x ( m o d p ) 1 ≡ a × x ( m o d p ) \begin{aligned}\frac{t}{a} \equiv t \times x\quad (\mod p) \\\frac{1}{a} \equiv 1 \times x\quad (\mod p) \\1 \equiv a \times x\quad (\mod p) \\\end{aligned} 由费马小定理:对于两个互质的整数
而言,一定有下式成立: g , h g,h
g h − 1 ≡ 1 ( m o d h ) g^{h-1} \equiv 1\quad (\mod h) 于是本题的推导就可以得到,当
与 a a 互质时,有: p p
a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \quad (\mod p) 于是
的乘法逆元 a a 就是: x x
x = a − 1 = a p − 2 x = a^{-1} = a^{p-2} 那么本道题就迎刃而解了。需要注意的是,上述乘法逆元的计算前提,即两个整数互质,由于其中一个数
一定是一个质数。因此判断 p p 与 a a 是否互质只需要判断 p p 是否是 a a 的倍数即可。 p p 时间复杂度:
n log x n \log x
1 | |
组合数
法一:利用递推式
思路:利用
时间复杂度:
1 | |
法二:利用乘法逆元
思路:除法转换为乘一个逆元
时间复杂度:
1 | |
字符串
sstream
控制中间结果的运算精度
1 | |
计算几何
浮点数默认输出 6 位,范围内的数据正常打印,最后一位四舍五入,范围外的数据未知。
]]>二分本质上是一个线性的算法思维,只是比线性思维更进一步的是,二分思维需要提炼出题面中两个线性相关的变量,即单调变化的两个变量,从而采用二分加速检索。
【二分答案】Building an Aquarium
https://codeforces.com/contest/1873/problem/E
题意:想象有一个二维平面,现在有一个数列,每一个数表示平面对应列的高度,现在要给这个平面在两边加上护栏,问护栏最高可以设置为多高,可以使得在完全填满的情况下,使用的水量不会超过给定的用水量。已知最大用水量为k
思路:对于一个护栏高度,水池高度低于护栏高度的地方都需要被水填满。为了便于分析,我们可以将水池高度进行排序。那么就会很显然的一个二分题目了,我们需要二分的就是护栏的高度(最小为1,最大需要考虑一下,就是只有一列的情况下,最大高度就是最高水池高度
),check的条件就是当前h的护栏高度时,消耗的水量与最大用水量之间的大小关系,如果超过了,那么高度就要下降,反之可以上升。由于是求最大高度,因此要使用的是求右边界的二分板子 max ( a i ) + m a x ( k ) \max(a_i)+max(k)
1 | |
【二分答案】分组
https://www.lanqiao.cn/problems/5129/learning/
题意:给定一个序列,现在需要将这个数列分为k组,如何分组可以使得每一组的极差中,最大值最小
最开始想到的思路:很容易联想到的一种方法其实就是高中组合数学中学到的“隔板法”,现在有n个数,需要分成k组,则方案数就是在n-1个空档中插入k-1个隔板,即
种方案 C n − 1 k − 1 C_{n-1}^{k-1} 时间复杂度
O ( n 2 ) O(n^2) 优化思路:上述思路是正向思维,即对于构思分组情况计算极差。我们不妨逆向思维,即枚举极差的情况,判断此时的分组情况。如果对于当前的极差lim,我们显然可以分成n组,即有一个最大分组值;我们也可以求一个最小分组值cnt,即如果再少分一组那么此时的极差就会超过当前约束的极差值lim。因此对于当前约束的极差值lim,我们可以求一个最小分组值cnt
- 如果当前的最小分组值cnt > k,那么
就无法包含k,也就是说当前约束的极差lim不符合条件,lim偏小 [ c n t , n ] \left [ cnt,n \right ] - 如果当前的最小分组值cnt <= k,那么
就一定包含k,且当前分组的最小极差一定是 <= 约束的极差值lim,lim偏大 [ c n t , n ] \left [ cnt,n \right ] 于是二分极差的思路就跃然纸上了。我们二分极差,然后根据可以分组的最小数量cnt判断二分的结果进行左右约束调整即可。
时间复杂度
O ( n log n ) O(n \log n)
1 | |
【二分答案】木材加工
https://www.luogu.com.cn/problem/P2440
题意:给定一个序列,现在需要将这个序列切分为等长的 k 段,长度必须为整数且尽可能的长,如果无法切分可以将多余的长度丢弃,问最长的长度是多少
思路:可以发现切分长度与切分的段数具有单调性,即切分的长度越长,切出来的段数就越少,可以进行二分。二分的思路就是直接二分答案,根据长度判断可切得的段数,最终套右边界的模板找到最大的长度即可。需要注意的是,对于无法切割的情况,就是需要切出的段数 k 超过了序列之和
时间复杂度:
O ( n log ( 1 e 8 ) ) O(n\log {(1e8)})
1 | |
【二分答案】跳石头
https://www.luogu.com.cn/problem/P2678
题意:给定 n 个递增的不重复数,现在可以从其中拿掉 k 个数,使得相邻数字之间的最小差值最大,问最大的最小差值是多少
思路:二分答案。将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。可以发现拿的数字越多,最小差值就越大,具有单调性,可以二分。我们直接二分答案,即直接二分最小差值的具体数值,通过判断当前的最小差值至少需要拿掉多少个数才能满足,进行 check 操作。至于如何计算至少要拿掉的数字,我们采用右贪心准则,即检查当前点与上一个点之间的距离是否满足最小差值的要求,如果不满足就需要记数,为了便于后续的计算,直接将当前的下标用上一个点的下标覆盖掉即可
时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【二分答案】路标设置
https://www.luogu.com.cn/problem/P3853
题意:与第四题题面几乎一致,只是现在不是从序列中拿走 k 数个,而是往序列中插入 k 个数(插入数字后要保证序列仍然没有重复数且递增),问在插入一定数量数字的情况下,最小的最大差值是多少
思路:**二分答案。将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。**同样可以发现,插入的数字越多,最大差值就越小,具有单调性,可以二分。我们依然直接二分答案,即直接二分最大差值的具体数值,通过判断当前的最大差值需要插入多少个数来检查当前状态是否合理。需要插入的数字的个数为:
⌈ a [ i ] − a [ i − 1 ] d i s t m a x ⌉ − 1 \left \lceil \frac{a[i]-a[i-1]}{dist_{max}}\right \rceil - 1 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【二分答案】数列分段 Section II
https://www.luogu.com.cn/problem/P1182
题意:给定一个无序的序列,现在需要将这个序列进行分段(连续的),分成指定的段数。问应该如何分段可以使得所有段的分段和的最大值最小,输出这个最小的最大值
思路:**二分答案,将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。**可以发现,分的段数越多,所有分段和的最大值就越小,具有单调性,可以二分。我们直接二分答案,即直接二分分段最大值,通过判断当前最大值的约束条件下可以分的组数进行判断。至于如何计算当前最大值条件下可分得的组数,直接线性扫描进行局部求和即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【二分答案】kotori的设备
https://www.luogu.com.cn/problem/P3743
题意:现在有一批电子设备,每一个电子设备有一个电量消耗速度与当前剩余电量,现在有一个充电器有一个确定的充电速度。问这批设备最久可以运作多久?当可以无限运作时输出 -1
思路:可以发现,想要运行的越久,需要补充的电量就越多,具有单调性,可以直接二分答案。很显然我们可以根据期望运行的时间进行 check 操作,通过比对当前期望时间可以充的电量与需要补充的电量进行比对来修改边界值。需要注意的是边界的选择,最长可运行时间为 1e10,具体 推导 待定
时间复杂度:
O ( n ( log 1 0 10 ) ) O(n(\log{10^{10})})
1 | |
【二分答案/并查集】关押罪犯 🔥
https://www.luogu.com.cn/problem/P1525
题意:给定一个无向图,没有重边和自环,边权为正。现在需要将图中所有的顶点分为两部分,使得两部分中最大的边权尽可能小,问该最小边权是多少
思路一:二分答案。
- 思路:本题一眼二分图问题,但是有些变化的是左右部并非散点图,其中是有连边的。如何求出最小边权呢?我们可以这么想,首先答案一定出自左右部的连边中(除非左右部全是散点,那答案就是 0),之所以可以采用二分图将点集分为两部分,是因为我们在某种规则下忽略了其中奇数环(二分图定理)的一些边。当规则定义为 忽略边权不超过 x 的边时,该图若可以二分,那么忽略边权比 x 值更大的边时,该图同样一定也可以二分,反之则不一定可以二分(特性图如下)。具备单调性,于是我们可以通过 二分阈值、检查图是否可二分 的方法来计算出答案
时间复杂度:
Θ ( log C m a x × ( n + e ) ) \Theta(\log C_{max} \times (n+e)) 思路二:并查集。
思路:
时间复杂度:
二分判定二分图代码:
1 | |
【二分答案】摆放棋子
https://www.acwing.com/problem/content/5562/
题意:给定一个 01 序列表示一个
的棋子序列,其中 1 表示有棋子,0 表示没有棋子。现在给定 k 个棋子,如何放置可以使得棋盘上连续的棋子长度尽可能长?给出一个合法的最长的序列 1 × n 1\times n 思路:可以发现,想要序列尽可能的长,那么需要放置的棋子就要尽可能的多,具备单调性,可以二分。我们二分答案,即最长序列长度。对于已知的 k 个可放置棋子,我们需要找到最大的序列长度,于是我们套用寻找右边界模板。检查方法就是判断对于当前的长度,通过前缀和与滑动窗口的形式计算当前窗口内需要放置多少颗棋子才能连为一体:
- 若需要的棋子数 < k,说明可以继续增大长度
- 若需要的棋子数 > k,说明当前长度无法满足,要缩小长度
- 若需要的棋子数 = k,归属在 < k 的类比中即可。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【二分答案】盖楼
https://www.acwing.com/problem/content/description/5569/
题意:给定 H 个正整数分别为 1 到 H。现在要将这 H 个正整数分给两个人,其中一个人希望获得可以不被 x 整除的数,另一个人希望可以获得不被 y 整除的数。其中 x 和 y 均为质数,问最小的 H 是多少?
思路:
很显然的一个二分答案。因为 H 越大,越有可能满足这两个人的要求,具备单调性。
那么现在的问题就是检查函数的设计。对于当前的高度 h,即 h 个正整数,很显然可以划分出下面的集合关系
其中 h-p-q+a 的部分两个人都可以获得。最策略是,p-a 与 q-a 的都给另外的人,如果不够,从 h-p-q+a 中拿,如果还不够那就说明当前 h 无法满足,需要增大 h,反之说明 h 可以满足,继续寻找答案的左边界。
时间复杂度:
Θ ( log ( N + M ) ) \Theta(\log (N+M))
1 | |
小插曲。一开始写的检查函数 code 始终只能通过 9/10,检查函数的代码如下:
1 | |
其实是因为有逻辑错误,即对于当前的 h,必须两个人都能满足才行。而上述代码可能会出现第一个人不满足,但是第二个人满足,却返回 true 的情况,而这是错误的。因此上述代码改成两个人同时满足就可以通过了,即如果有一个人不满足,则返回 false:
1 | |
小结:过多的分支语句不如一个 max 来的更加清晰,也可以避免一定的逻辑错误。
【二分答案】找出叠涂元素
https://leetcode.cn/problems/first-completely-painted-row-or-column/description/
题意:给定一个
的矩阵,以及一个存储矩阵中所有元素值的数组,现在从左往右将数组中的元素在对应矩阵中涂色,问序列中最左边使得矩阵中某一行或列全部涂色的下标是什么 m × n m\times n 思路:显然,下标越往右越有可能出现矩阵中某一行或列全部涂色,具备单调性,可以二分答案。我们直接二分序列下标,对于 chk 函数我们直接
模拟即可 O ( n × m ) O(n\times m) 时间复杂度:
O ( n × m log ( n × m ) ) O(n\times m \log (n\times m))
1 | |
【二分答案/双指针】找出唯一性数组的中位数
https://leetcode.cn/problems/find-the-median-of-the-uniqueness-array/
题意:给定一个数组,返回其「唯一性数组」的中位数。如果唯一性数组有奇数个元素,则返回中间元素,如果有偶数个元素,则返回两个中间元素中较小的那个,即左边那个中间元素。唯一性数组定义为:原数组的所有非空子数组中不同元素的个数组成的序列。
思路:
- 首先根据题意可以明确的计算出这个唯一性数组的元素个数
。假设原数组有 t o t tot 个元素,则其唯一性数组一定有 n n 个元素,且最小值一定是 t o t = ( 1 + n ) × n 2 \displaystyle tot=\frac{(1+n) \times n}{2} ,最大值 1 1 。最暴力的做法就是 ≤ n \le n 的维护出这个唯一性数组然后返回其中位数,但这对于 O ( n 2 ) O(n^2) 级别的数据显然是不合适的。观察其他性质。 1 0 5 10^5 - 不难发现,对于「不同元素的个数
」而言, x x 越大,满足条件的子数组数量就越多,反之 x x 越小,则满足条件的子数组数量就越少,具备单调性,考虑二分。 x x - 问题就是在
内找到一个尽可能小的 [ 1 , n ] [1,n] 使得满足「不同元素的个数 u p p e r upper 的子数组」的数量 ≤ u p p e r \le upper 。 ≥ ⌈ t o t 2 ⌉ \displaystyle \ge \lceil \frac{tot}{2} \rceil - 我们能否在指定不同元素个数上限为
的情况下,快速计算合法子数组的个数呢?答案是可以的,我们引入双指针算法进行 u p p e r upper 的 O ( n ) O(n) 。我们枚举子数组的右边界并利用哈希表维护子数组的左边界进行统计即可。 c h e c k check 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
1 | |
【二分查找】Bomb
https://codeforces.com/contest/1996/problem/F
题意:给定两个序列
和 a a 以及最大操作次数 b b ,问在不超过最大操作次数的情况下,最多可以获得多少收益?收益的计算方法为:每次选择 k k 中一个数 a a a[i]加入收益,并将该数减去b[i]直到为。 0 0 思路:
- 暴力抬手:最暴力的做法是我们每次操作时选择
中的最大值进行计数并对其修改,但是显然 a a 会超时,我们考虑加速这个过程。 O ( n k ) O(nk) - 加速进程:由于最终结果中每次操作都是最优的,因此操作次数越多获得的收益就越大,具备单调性。如何利用这个单调性呢?关键在于全体数据的操作次数,我们记作
。假设我们对 k ′ k' 中全体数据可取的范围设置一个下限 a a ,那么显然的 l o w e r lower 越高, l o w e r lower 越小, k ′ k' 越低, l o w e r lower 越大。于是根据单调的传递性可知 k ′ k' 也和最终的收益具备单调性, l o w e r lower 越高,收益越小, l o w e r lower 越低,收益越大。因此我们二分 l o w e r lower ,使得 l o w e r lower 左逼近 k ′ k' 。 k k - 细节处理:二分的边界是什么?这需要从计算最终结果的角度来思考。对于二分出的下界
,即 l o w e r lower ,此时扫描一遍计算出来的操作次数 r r 一定是 k ′ k' 。也就是说我们还需要操作 k ′ ≤ k k'\le k 次,显然我们可以将每个数操作后维护到最终的结果,然后执行上述的暴力思路,但是这样仍然会超时,因为 k − k ′ k-k' 的计算结果最大是 k − k ′ k-k' ,此时进行暴力仍然会达到 n n 。正难则反,我们不妨将上述二分出的 O ( n 2 ) O(n^2) 减一进行最终答案的计算,这样对应的操作次数 l o w e r lower 一定会超过 k ′ k' ,并且对于超过 k k 的操作,累加到答案的数值一定都是 k k ,这一步也是本题最精妙的一步。从上述分析不难发现,二分的下界需要设定为 l o w e r − 1 lower-1 ,因为后续累加答案时会对 1 1 进行减一操作;二分的上界需要设定为严格大于 l o w e r lower 的数,比如 1 0 9 10^9 ,因为我们需要保证 1 0 9 + 1 10^9+1 后对应的操作次数 l o w e r − 1 lower-1 严格大于 k ′ k' 。 k k 时间复杂度:
O ( n log k ) O(n\log k)
1 | |
将大问题转化为等价小问题进行求解。
【分治】随机排列
https://www.acwing.com/problem/content/5469/
题意:给定一个 n 个数的全排列序列,并将其进行一定的对换,问是对换了 3n 次还是 7n+1 次
思路:可以发现对于两种情况,就对应对换次数的奇偶性。当 n 为奇数:3n 为奇数,7n+1 为偶数;当 n 为偶数:3n 为偶数,7n+1 为奇数。故我们只需要判断序列的逆序数即可。为了求解逆序数,我们可以采用归并排序的 combine 过程进行统计即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
优雅的解法,少不了优雅的板子。目前仅编写 C++ 和 Python 语言对应的板子。前者用于备赛 Xcpc,后者用于备赛蓝桥杯。
基础算法
高精度
1 | |
二分
闭区间寻找左边界:
1 | |
闭区间寻找右边界:
1 | |
哈希
使用 std::unordered_map 时可能会因为哈希冲突导致查询、插入操作降低到 std::map 进行替代,或者自定义一个哈希函数。
1 | |
数据结构
并查集
1 | |
1 | |
树状数组
1 | |
1 | |
SortedList
有序列表,改编于 from sortedcontainers import SortedList,共有以下内容:
- 公开方法:全部都是
O ( log n ) O(\log n) add(value): 添加一个值到有序列表discard(value): 删除列表中的值(如果存在)remove(value): 删除列表中的值(必须存在)pop(index=-1): 删除并返回指定索引处的值bisect_left(value): 返回插入值的最左索引bisect_right(value): 返回插入值的最右索引count(value): 计算值在列表中的出现次数
- 魔法方法
__init__():初始化传入一个可迭代对象__len__(): 返回列表的长度__getitem__(index): 获取指定索引处的值 -O ( log n ) O(\log n) __delitem__(index): 删除指定索引处的值 -O ( log n ) O(\log n) __contains__(value): 检查值是否在列表中 -O ( log n ) O(\log n) __iter__(): 返回列表的迭代器__reversed__(): 返回列表的反向迭代器__repr__(): 返回列表的字符串表示形式
1 | |
引自:https://www.acwing.com/activity/content/code/content/8475415/
官方:https://github.com/grantjenks/python-sortedcontainers/blob/master/src/sortedcontainers/sortedlist.py
数学
模运算
1 | |
质数筛
1 | |
乘法逆元
之所以需要知道一个数
的乘法逆元,是为了将除法在模 a a 的前提下转化为乘法,从而简化运算。推导 p p 的乘法逆元的逻辑如下: a a
对于任意
的整数倍 a a ,一定有下式成立:其中的 t t 就是整数 x x 的乘法逆元,记作 a a a − 1 a^{-1}
t a ≡ t × x ( m o d p ) 1 a ≡ 1 × x ( m o d p ) 1 ≡ a × x ( m o d p ) \begin{aligned}\frac{t}{a} \equiv t \times x\quad (\mod p) \\\frac{1}{a} \equiv 1 \times x\quad (\mod p) \\1 \equiv a \times x\quad (\mod p) \\\end{aligned} 由费马小定理:对于两个互质的整数
而言,一定有下式成立: g , h g,h
g h − 1 ≡ 1 ( m o d h ) g^{h-1} \equiv 1\quad (\mod h) 于是本题的推导就可以得到,当
与 a a 互质时,有: p p
a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \quad (\mod p) 于是
的乘法逆元 a a 就是: x x
x = a − 1 = a p − 2 x = a^{-1} = a^{p-2} 那么本道题就迎刃而解了。需要注意的是,上述乘法逆元的计算前提,即两个整数互质,由于其中一个数
一定是一个质数。因此判断 p p 与 a a 是否互质只需要判断 p p 是否是 a a 的倍数即可。 p p 时间复杂度:
n log x n \log x
1 | |
组合数
法一:利用递推式
思路:利用
时间复杂度:
1 | |
法二:利用乘法逆元
思路:除法转换为乘一个逆元
时间复杂度:
1 | |
字符串
sstream
控制中间结果的运算精度
1 | |
计算几何
浮点数默认输出 6 位,范围内的数据正常打印,最后一位四舍五入,范围外的数据未知。
]]>二分本质上是一个线性的算法思维,只是比线性思维更进一步的是,二分思维需要提炼出题面中两个线性相关的变量,即单调变化的两个变量,从而采用二分加速检索。
【二分答案】Building an Aquarium
https://codeforces.com/contest/1873/problem/E
题意:想象有一个二维平面,现在有一个数列,每一个数表示平面对应列的高度,现在要给这个平面在两边加上护栏,问护栏最高可以设置为多高,可以使得在完全填满的情况下,使用的水量不会超过给定的用水量。已知最大用水量为k
思路:对于一个护栏高度,水池高度低于护栏高度的地方都需要被水填满。为了便于分析,我们可以将水池高度进行排序。那么就会很显然的一个二分题目了,我们需要二分的就是护栏的高度(最小为1,最大需要考虑一下,就是只有一列的情况下,最大高度就是最高水池高度
),check的条件就是当前h的护栏高度时,消耗的水量与最大用水量之间的大小关系,如果超过了,那么高度就要下降,反之可以上升。由于是求最大高度,因此要使用的是求右边界的二分板子 max ( a i ) + m a x ( k ) \max(a_i)+max(k)
1 | |
【二分答案】分组
https://www.lanqiao.cn/problems/5129/learning/
题意:给定一个序列,现在需要将这个数列分为k组,如何分组可以使得每一组的极差中,最大值最小
最开始想到的思路:很容易联想到的一种方法其实就是高中组合数学中学到的“隔板法”,现在有n个数,需要分成k组,则方案数就是在n-1个空档中插入k-1个隔板,即
种方案 C n − 1 k − 1 C_{n-1}^{k-1} 时间复杂度
O ( n 2 ) O(n^2) 优化思路:上述思路是正向思维,即对于构思分组情况计算极差。我们不妨逆向思维,即枚举极差的情况,判断此时的分组情况。如果对于当前的极差lim,我们显然可以分成n组,即有一个最大分组值;我们也可以求一个最小分组值cnt,即如果再少分一组那么此时的极差就会超过当前约束的极差值lim。因此对于当前约束的极差值lim,我们可以求一个最小分组值cnt
- 如果当前的最小分组值cnt > k,那么
就无法包含k,也就是说当前约束的极差lim不符合条件,lim偏小 [ c n t , n ] \left [ cnt,n \right ] - 如果当前的最小分组值cnt <= k,那么
就一定包含k,且当前分组的最小极差一定是 <= 约束的极差值lim,lim偏大 [ c n t , n ] \left [ cnt,n \right ] 于是二分极差的思路就跃然纸上了。我们二分极差,然后根据可以分组的最小数量cnt判断二分的结果进行左右约束调整即可。
时间复杂度
O ( n log n ) O(n \log n)
1 | |
【二分答案】木材加工
https://www.luogu.com.cn/problem/P2440
题意:给定一个序列,现在需要将这个序列切分为等长的 k 段,长度必须为整数且尽可能的长,如果无法切分可以将多余的长度丢弃,问最长的长度是多少
思路:可以发现切分长度与切分的段数具有单调性,即切分的长度越长,切出来的段数就越少,可以进行二分。二分的思路就是直接二分答案,根据长度判断可切得的段数,最终套右边界的模板找到最大的长度即可。需要注意的是,对于无法切割的情况,就是需要切出的段数 k 超过了序列之和
时间复杂度:
O ( n log ( 1 e 8 ) ) O(n\log {(1e8)})
1 | |
【二分答案】跳石头
https://www.luogu.com.cn/problem/P2678
题意:给定 n 个递增的不重复数,现在可以从其中拿掉 k 个数,使得相邻数字之间的最小差值最大,问最大的最小差值是多少
思路:二分答案。将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。可以发现拿的数字越多,最小差值就越大,具有单调性,可以二分。我们直接二分答案,即直接二分最小差值的具体数值,通过判断当前的最小差值至少需要拿掉多少个数才能满足,进行 check 操作。至于如何计算至少要拿掉的数字,我们采用右贪心准则,即检查当前点与上一个点之间的距离是否满足最小差值的要求,如果不满足就需要记数,为了便于后续的计算,直接将当前的下标用上一个点的下标覆盖掉即可
时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【二分答案】路标设置
https://www.luogu.com.cn/problem/P3853
题意:与第四题题面几乎一致,只是现在不是从序列中拿走 k 数个,而是往序列中插入 k 个数(插入数字后要保证序列仍然没有重复数且递增),问在插入一定数量数字的情况下,最小的最大差值是多少
思路:**二分答案。将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。**同样可以发现,插入的数字越多,最大差值就越小,具有单调性,可以二分。我们依然直接二分答案,即直接二分最大差值的具体数值,通过判断当前的最大差值需要插入多少个数来检查当前状态是否合理。需要插入的数字的个数为:
⌈ a [ i ] − a [ i − 1 ] d i s t m a x ⌉ − 1 \left \lceil \frac{a[i]-a[i-1]}{dist_{max}}\right \rceil - 1 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【二分答案】数列分段 Section II
https://www.luogu.com.cn/problem/P1182
题意:给定一个无序的序列,现在需要将这个序列进行分段(连续的),分成指定的段数。问应该如何分段可以使得所有段的分段和的最大值最小,输出这个最小的最大值
思路:**二分答案,将答案看做 y 轴,拿掉的数的数量看做 x 轴,就是二分 y 值。**可以发现,分的段数越多,所有分段和的最大值就越小,具有单调性,可以二分。我们直接二分答案,即直接二分分段最大值,通过判断当前最大值的约束条件下可以分的组数进行判断。至于如何计算当前最大值条件下可分得的组数,直接线性扫描进行局部求和即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【二分答案】kotori的设备
https://www.luogu.com.cn/problem/P3743
题意:现在有一批电子设备,每一个电子设备有一个电量消耗速度与当前剩余电量,现在有一个充电器有一个确定的充电速度。问这批设备最久可以运作多久?当可以无限运作时输出 -1
思路:可以发现,想要运行的越久,需要补充的电量就越多,具有单调性,可以直接二分答案。很显然我们可以根据期望运行的时间进行 check 操作,通过比对当前期望时间可以充的电量与需要补充的电量进行比对来修改边界值。需要注意的是边界的选择,最长可运行时间为 1e10,具体 推导 待定
时间复杂度:
O ( n ( log 1 0 10 ) ) O(n(\log{10^{10})})
1 | |
【二分答案/并查集】关押罪犯 🔥
https://www.luogu.com.cn/problem/P1525
题意:给定一个无向图,没有重边和自环,边权为正。现在需要将图中所有的顶点分为两部分,使得两部分中最大的边权尽可能小,问该最小边权是多少
思路一:二分答案。
- 思路:本题一眼二分图问题,但是有些变化的是左右部并非散点图,其中是有连边的。如何求出最小边权呢?我们可以这么想,首先答案一定出自左右部的连边中(除非左右部全是散点,那答案就是 0),之所以可以采用二分图将点集分为两部分,是因为我们在某种规则下忽略了其中奇数环(二分图定理)的一些边。当规则定义为 忽略边权不超过 x 的边时,该图若可以二分,那么忽略边权比 x 值更大的边时,该图同样一定也可以二分,反之则不一定可以二分(特性图如下)。具备单调性,于是我们可以通过 二分阈值、检查图是否可二分 的方法来计算出答案
时间复杂度:
Θ ( log C m a x × ( n + e ) ) \Theta(\log C_{max} \times (n+e)) 思路二:并查集。
思路:
时间复杂度:
二分判定二分图代码:
1 | |
【二分答案】摆放棋子
https://www.acwing.com/problem/content/5562/
题意:给定一个 01 序列表示一个
的棋子序列,其中 1 表示有棋子,0 表示没有棋子。现在给定 k 个棋子,如何放置可以使得棋盘上连续的棋子长度尽可能长?给出一个合法的最长的序列 1 × n 1\times n 思路:可以发现,想要序列尽可能的长,那么需要放置的棋子就要尽可能的多,具备单调性,可以二分。我们二分答案,即最长序列长度。对于已知的 k 个可放置棋子,我们需要找到最大的序列长度,于是我们套用寻找右边界模板。检查方法就是判断对于当前的长度,通过前缀和与滑动窗口的形式计算当前窗口内需要放置多少颗棋子才能连为一体:
- 若需要的棋子数 < k,说明可以继续增大长度
- 若需要的棋子数 > k,说明当前长度无法满足,要缩小长度
- 若需要的棋子数 = k,归属在 < k 的类比中即可。
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【二分答案】盖楼
https://www.acwing.com/problem/content/description/5569/
题意:给定 H 个正整数分别为 1 到 H。现在要将这 H 个正整数分给两个人,其中一个人希望获得可以不被 x 整除的数,另一个人希望可以获得不被 y 整除的数。其中 x 和 y 均为质数,问最小的 H 是多少?
思路:
很显然的一个二分答案。因为 H 越大,越有可能满足这两个人的要求,具备单调性。
那么现在的问题就是检查函数的设计。对于当前的高度 h,即 h 个正整数,很显然可以划分出下面的集合关系
其中 h-p-q+a 的部分两个人都可以获得。最策略是,p-a 与 q-a 的都给另外的人,如果不够,从 h-p-q+a 中拿,如果还不够那就说明当前 h 无法满足,需要增大 h,反之说明 h 可以满足,继续寻找答案的左边界。
时间复杂度:
Θ ( log ( N + M ) ) \Theta(\log (N+M))
1 | |
小插曲。一开始写的检查函数 code 始终只能通过 9/10,检查函数的代码如下:
1 | |
其实是因为有逻辑错误,即对于当前的 h,必须两个人都能满足才行。而上述代码可能会出现第一个人不满足,但是第二个人满足,却返回 true 的情况,而这是错误的。因此上述代码改成两个人同时满足就可以通过了,即如果有一个人不满足,则返回 false:
1 | |
小结:过多的分支语句不如一个 max 来的更加清晰,也可以避免一定的逻辑错误。
【二分答案】找出叠涂元素
https://leetcode.cn/problems/first-completely-painted-row-or-column/description/
题意:给定一个
的矩阵,以及一个存储矩阵中所有元素值的数组,现在从左往右将数组中的元素在对应矩阵中涂色,问序列中最左边使得矩阵中某一行或列全部涂色的下标是什么 m × n m\times n 思路:显然,下标越往右越有可能出现矩阵中某一行或列全部涂色,具备单调性,可以二分答案。我们直接二分序列下标,对于 chk 函数我们直接
模拟即可 O ( n × m ) O(n\times m) 时间复杂度:
O ( n × m log ( n × m ) ) O(n\times m \log (n\times m))
1 | |
【二分答案/双指针】找出唯一性数组的中位数
https://leetcode.cn/problems/find-the-median-of-the-uniqueness-array/
题意:给定一个数组,返回其「唯一性数组」的中位数。如果唯一性数组有奇数个元素,则返回中间元素,如果有偶数个元素,则返回两个中间元素中较小的那个,即左边那个中间元素。唯一性数组定义为:原数组的所有非空子数组中不同元素的个数组成的序列。
思路:
- 首先根据题意可以明确的计算出这个唯一性数组的元素个数
。假设原数组有 t o t tot 个元素,则其唯一性数组一定有 n n 个元素,且最小值一定是 t o t = ( 1 + n ) × n 2 \displaystyle tot=\frac{(1+n) \times n}{2} ,最大值 1 1 。最暴力的做法就是 ≤ n \le n 的维护出这个唯一性数组然后返回其中位数,但这对于 O ( n 2 ) O(n^2) 级别的数据显然是不合适的。观察其他性质。 1 0 5 10^5 - 不难发现,对于「不同元素的个数
」而言, x x 越大,满足条件的子数组数量就越多,反之 x x 越小,则满足条件的子数组数量就越少,具备单调性,考虑二分。 x x - 问题就是在
内找到一个尽可能小的 [ 1 , n ] [1,n] 使得满足「不同元素的个数 u p p e r upper 的子数组」的数量 ≤ u p p e r \le upper 。 ≥ ⌈ t o t 2 ⌉ \displaystyle \ge \lceil \frac{tot}{2} \rceil - 我们能否在指定不同元素个数上限为
的情况下,快速计算合法子数组的个数呢?答案是可以的,我们引入双指针算法进行 u p p e r upper 的 O ( n ) O(n) 。我们枚举子数组的右边界并利用哈希表维护子数组的左边界进行统计即可。 c h e c k check 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
1 | |
【二分查找】Bomb
https://codeforces.com/contest/1996/problem/F
题意:给定两个序列
和 a a 以及最大操作次数 b b ,问在不超过最大操作次数的情况下,最多可以获得多少收益?收益的计算方法为:每次选择 k k 中一个数 a a a[i]加入收益,并将该数减去b[i]直到为。 0 0 思路:
- 暴力抬手:最暴力的做法是我们每次操作时选择
中的最大值进行计数并对其修改,但是显然 a a 会超时,我们考虑加速这个过程。 O ( n k ) O(nk) - 加速进程:由于最终结果中每次操作都是最优的,因此操作次数越多获得的收益就越大,具备单调性。如何利用这个单调性呢?关键在于全体数据的操作次数,我们记作
。假设我们对 k ′ k' 中全体数据可取的范围设置一个下限 a a ,那么显然的 l o w e r lower 越高, l o w e r lower 越小, k ′ k' 越低, l o w e r lower 越大。于是根据单调的传递性可知 k ′ k' 也和最终的收益具备单调性, l o w e r lower 越高,收益越小, l o w e r lower 越低,收益越大。因此我们二分 l o w e r lower ,使得 l o w e r lower 左逼近 k ′ k' 。 k k - 细节处理:二分的边界是什么?这需要从计算最终结果的角度来思考。对于二分出的下界
,即 l o w e r lower ,此时扫描一遍计算出来的操作次数 r r 一定是 k ′ k' 。也就是说我们还需要操作 k ′ ≤ k k'\le k 次,显然我们可以将每个数操作后维护到最终的结果,然后执行上述的暴力思路,但是这样仍然会超时,因为 k − k ′ k-k' 的计算结果最大是 k − k ′ k-k' ,此时进行暴力仍然会达到 n n 。正难则反,我们不妨将上述二分出的 O ( n 2 ) O(n^2) 减一进行最终答案的计算,这样对应的操作次数 l o w e r lower 一定会超过 k ′ k' ,并且对于超过 k k 的操作,累加到答案的数值一定都是 k k ,这一步也是本题最精妙的一步。从上述分析不难发现,二分的下界需要设定为 l o w e r − 1 lower-1 ,因为后续累加答案时会对 1 1 进行减一操作;二分的上界需要设定为严格大于 l o w e r lower 的数,比如 1 0 9 10^9 ,因为我们需要保证 1 0 9 + 1 10^9+1 后对应的操作次数 l o w e r − 1 lower-1 严格大于 k ′ k' 。 k k 时间复杂度:
O ( n log k ) O(n\log k)
1 | |
无论是深搜还是宽搜,都逃不掉图的思维。我们将搜索图建立起来之后,剩余的编码过程就会跃然纸上。
【dfs】机器人的运动范围
https://www.acwing.com/problem/content/22/
1 | |
【dfs】CCC单词搜索
https://www.acwing.com/problem/content/5168/
搜索逻辑:分为正十字与斜十字
更新答案逻辑:需要进行两个条件的约数,一个是是否匹配到了最后一个字母,一个是转弯次数不超过一次
转弯判断逻辑:
首先不能是起点开始的
对于正十字:如果next的行 & 列都与pre的行和列不相等,就算转弯
对于斜十字:如果next的行 | 列有和pre相等的,就算转弯
1 | |
【dfs/二进制枚举】数量
https://www.acwing.com/problem/content/5150/
题意:给定一个数n,问[1, n]中有多少个数只含有4或7
思路一:dfs
- 对于一个数,我们可以构造一个二叉搜数进行搜索,因为每一位只有两种可能,那么从最高位开始搜索。如果当前数超过了n就return,否则就算一个答案
- 时间复杂度:
Θ ( 2 1 + lg ( max ( a [ i ] ) ) ) \Theta(2^{1 + \lg{(\max(a[i])})}) 思路二:二进制枚举
- 按照数位进行计算。对于一个 x 位的数,1 到 x-1 位的情况下所有的数都符合条件,对于一个 t 位的数,满情况就是
种,所以 2 t 2^t [1,x-1]位就一共有种情况 。对于第 x 位,采取二进制枚举与原数进行比较,如果小于原数,则答案 +1,反之结束循环输出答案即可 2 1 + 2 2 + ⋯ + 2 x − 1 = 2 x − 2 2^1 + 2^2 + \cdots + 2^{x - 1} = 2^{x} - 2
dfs 代码:
1 | |
二进制枚举代码:
1 | |
【dfs】组合总和
https://leetcode.cn/problems/combination-sum/
题意:给定一个序列,其中的元素没有重复,问如何选取其中的元素,使得选出的数字总和为指定的数字target,选取的数字可以重复
思路:思路比较简答,很容易想到用dfs搜索出所有的组合情况,即对于每一个“结点”,我们直接遍历序列中的元素即可。但是由于题目的限制,即不允许合法的序列经过排序后相等。那么为了解决这个约束,我们可以将最终搜索到的序列排序后进行去重,但是这样的时间复杂度会很高,于是我们从搜索的过程切入。观看这一篇题解 防止出现重复序列的启蒙题解,我们提取其中最关键的一个图解
可见3,4和4,3的剩余选项(其中可能包含了答案序列)全部重复,因此我们直接减去这个枝即可。不难发现,我们根据上述优化思想,剪枝的操作可以为:让当前序列开始枚举的下标
idx从上一层开始的下标i开始,于是剪枝就可以实现了。时间复杂度:
Θ ( 2 n log n ) \Theta \left ( 2^{\frac{n}{\log n}}\right)
1 | |
【递归】扩展字符串
https://www.acwing.com/problem/content/5284/
题意:给定一种字符串的构造方式,问构造n次以后的字符串中的第k个字符是什么
思路:由于构造的方法是基于上一种情况的,很容易可以想到一个递归搜索树来解决。只是这道题有好几个坑,故记录一下。
- 首先说一下搜索的思路:对于当前的状态,我们想要知道第k个位置上的字符,很显然我们可以通过预处理每一种构造状态下的字符串长度得到下一个字符串的长度,于是我们可以在当前的字符串中,通过比对下标与五段字符串长度的大小,来确定是继续递归还是直接输出
- 特判:可以发现,对于
的情况,我们无法采用相同的结构进行计算,故进行特判,如果当前来到了最初始的字符串状态,我们直接输出相应位置上的字符即可 n = 0 n=0 - 最后说一下递归终点的设计:与搜索所有的答案情况不同,这道题的答案是唯一的,因此我们在搜索到答案后,可以通过一个
bool变量作为一个标记,表示已经找到答案了,只需要不断回溯直到回溯结束为止,就不需要再遍历其他的分支了- **坑:**这道题的坑说实话有点难崩。
- 首先是一个k的大小,是一定要开
long long的,我一开始直接全局宏定义int为long long了- 还有一个坑可能是只要我才会犯的,就是字符串按照下标输出字符的时候,是需要
-1的,闹心的是我有的加了,有的没加,还是debug的时候调出来的- 最后一个大坑,属于是引以为戒了。就是这句
len[i] = min(len[i], (int)2e18),因为我们可以发现,抛开那三个固定长度的字符串来说,每一次新构造出来的字符串长度都是上一个字符串长度倍,那么构造 2 2 次后的字符串长度就是 n n 长度的 s 0 s_0 倍,那么对于 2 n 2^n 的取值范围来说,直接存储长度肯定是不可取的。那么如何解决这个问题呢?方法是我们对 n n len[i]进行一个约束即可,见代码。最后进行递归比较长度就没问题了。- 时间复杂度:
- 由于每一个构造的状态我们都是常数级别的比较,因此相当于一个状态的搜索时间复杂度为 O ( n ) O(n) ,那么总合就是 O ( 1 ) O(1) O ( n ) O(n)
1 | |
【dfs】让我们异或吧
https://www.luogu.com.cn/problem/P2420
题意:给定一棵树,树上每一条边都有一个权值,现在有Q次询问,对于每次询问会给出两个结点编号u,v,需要输出结点u到结点v所经过的路径的所有边权的异或之和
思路:对于每次询问,我们当然可以遍历从根到两个结点的所有边权,然后全部异或计算结果,但是时间复杂度是
,显然不行,那么有什么优化策略吗?答案是有的。我们可以发现,对于两个结点之间的所有边权,其实就是根到两个结点的边权相异或得到的结果(异或的性质),我们只需要预处理出根结点到所有结点的边权已异或值,后续询问的时候直接 O ( n ) O(n) 计算即可 O ( 1 ) O(1) 时间复杂度:
Θ ( n + q ) \Theta(n+q)
1 | |
【记忆化搜索】Function
https://www.luogu.com.cn/problem/P1464
题意:
思路一:直接dfs
- 直接按照题意进行dfs代码的编写,但是很显然时间复杂极高
- 时间复杂度:
O ( T × 情况数 ) O(T \times \text{情况数}) 思路二:记忆化dfs
- 记忆化逻辑:
- 如果当前的状态没有记忆过,就记忆一下
- 如果当前的状态已经记忆过了,就不需要继续递归搜索了,直接使用之前已经记忆过的答案即可
- 上述起始状态需要和搜到答案的状态做一个区别。我们知道,对于一组合法的输入,答案一定是
- 注意点:
- 输入终止条件不是
a != -1 && b != -1 && c != -1,而是要三者都不是-1才行- 对于每一组输入,我们不需要
memset记忆数组,因为每一组的记忆依赖是相同的- 由于答案一定是
的,因此是否记忆过只需要看当前状态的答案是否 > 0 >0 即可 > 0 >0 - 时间复杂度:
< O ( T × n 3 ) <O(T \times n^3)
直接dfs代码:
1 | |
记忆化dfs代码:
1 | |
【递归】外星密码
https://www.luogu.com.cn/problem/P1928
线性递归
题意:给定一个压缩后的密码串,需要解压为原来的形式。压缩形式距离
AC[3FUN]→ \to ACFUNFUNFUNAB[2[2GH]]OP→ \to ABGHGHGHGHOP思路:
我们采用递归的策略
我们知道,对于每一个字符,一共有4种情况,分别是:“字母”、“数字”、“[”、“]”。如果是字母。我们分情况考虑
- “字母”:
- 直接加入答案字符串即可
- “[”:
- 获取左括号后面的整体 - 采用递归策略获取后面的整体
- 加入答案字符串
- “数字”:
- 获取完整的数 - 循环小trick
- 获取数字后面的整体 - 采用递归策略获取后面的整体
- 加入答案字符串 - 循环尾加入即可
- 返回当前的答案字符串
- “]”:
- 返回当前的答案字符串 - 与上述 “[” 对应
代码设计分析:
我们将压缩后的字符串看成由下面两种单元组成:
- 最外层中括号组成的单元:如
[2[2AB]]就算一个最外层中括号组成的单元- 连续的字母单元:如
OPQ就算一个连续的字母单元解决各单元连接问题:
为了在递归处理完第一种单元后还能继续处理后续的第二种单元,我们直接按照压缩字符串的长度进行遍历,即
while (i < s.size())操作解决两种单元内部问题:
- 最外层中括号组成的单元:递归处理
- 连续的字母单元:直接加入当前答案字符串即可
手玩样例:
- 显然按照定义,上述压缩字符串一共有五个单元
- 我们用红色表示进入递归,蓝色表示驱动递归结束并回溯。可以发现
时间复杂度:
Θ ( res.length() ) \Theta(\text{res.length()})
1 | |
【dfs+剪枝/二进制枚举】选数
https://www.luogu.com.cn/problem/P1036
题意:给定n个数,从中选出k个数,问一共有多少种方案可以使得选出来的k个数之和为质数
思路一:dfs+剪枝
- 按照数据量可以直接暴搜,搜索依据是每一个数有两种状态,即选和不选,于是搜索树就是一棵二叉树
- 搜索状态定义为:对于当前第idx个数,已经选择了cnt个数,已经选择的数之和为sum
- 搜索终止条件为:idx越界
- 剪枝:已经选择了k个数就直接返回,不用再选剩下的数了
- 时间复杂度:
- 剪枝后一定是小于这个复杂度的 O ( 2 n ) O(2^n) 思路二:二进制枚举
- 直接枚举
,按照其中含有的 0 → 2 n − 1 0\to 2^n-1 的个数,来进行选数判断 1 1 - 时间复杂度:
- 一定会跑满的 O ( 2 n ) O(2^n)
dfs+剪枝
1 | |
二进制枚举
1 | |
【dfs/bfs】01迷宫
https://www.luogu.com.cn/problem/P1141
题意:给定一个01矩阵,行走规则为“可以走到相邻的数字不同的位置”,现在给定m次询问
(u,v),输出从(u,v)开始最多可以走多少个位置?思路:我们可以将此问题转化为一个求解连通块的问题。对于矩阵中的一个连通块,我们定义为:在其中任意一个位置开始行走,都可以走过整个连通块每一个位置。那么在询问时,只需要输出所在连通块元素的个数即可。现在将问题转化为了
如何遍历每一个连通块?按照标记数组的情况,如果一个位置没有被标记,就从这个位置出发开始打标记并统计
如何统计每一个连通块中元素的个数?按照题目中给定的迷宫行走规则,可以通过bfs或者dfs实现遍历
bfs代码
1 | |
dfs代码
1 | |
【dfs/二进制枚举】kkksc03考前临时抱佛脚
https://www.luogu.com.cn/problem/P2392
题意:给定四组数据,每组数据由 n 个数字组成,对于每一组数字需要分为两组使得两组之和相差尽可能小,问最终四组数据分组后,每一组之和的最大值之和是多少
思路一:二进制枚举
可以发现,我们可以只设计处理一组数据的算法,其余组数的数据调用该算法即可。对于一个序列,想要将其划分为 2 组使得 2 组之和的差值最小,我们可以发现,对于序列中的一个数而言,有两个状态,要么分到第一组,要么就分到第二组,因此我们可以采用二进制枚举的方式,将所有的分组情况全部枚举出来,每一个状态计算一下和的差值,最后取最小差值时,两组中和的最大值即可
时间复杂度:
O ( 4 × 2 n ) O(4 \times 2^n) 思路二:dfs
从上面的二进制枚举得到启发,一定可以进行二叉树搜索。很显然就直接左结点让当前数分到左组,右结点让当前数分到右组即可。本题无法剪枝,因为两组之和的差值没有规律
时间复杂度:
O ( 4 × 2 n ) O(4 \times 2^n)
二进制枚举代码
1 | |
dfs代码
1 | |
【dfs/二进制枚举】PERKET
https://www.luogu.com.cn/problem/P2036
题意:给定一个二元组序列,每一个二元组中,一个表示酸度,一个表示苦度,现在在至少需要选择一个二元组的情况下,希望酸度之积与苦度之和的差值最小
思路一:二进制枚举
很显然的一个二进制枚举。每一个二元组都只有两个状态,即被选择 or 不被选择,故可采用二进制枚举,对于每一个状态统计酸度之积与苦度之和即可
时间复杂度:
O ( 2 n ) O(2^n) 思路二:dfs
按照上述二进制枚举的思路进行模拟即可,本题无法剪枝,因为酸度与苦度之差没有规律
时间复杂度:
O ( 2 n ) O(2^n)
二进制枚举代码
1 | |
dfs代码
1 | |
【dfs】迷宫
https://www.luogu.com.cn/problem/P1605
题意:矩阵寻路,有障碍物,每一个点只能走一次,找到起点到终点可达路径数
思路:其实就是一个四叉树的题目,只需要进行四个方向的遍历搜索即可找到路径,由于会进行:越界、障碍物、以及不可重复遍历的剪枝,故遍历的数量会很少
时间复杂度:
< < O ( 4 n m ) << O(4^{nm})
1 | |
【dfs】单词方阵
https://www.luogu.com.cn/problem/P1101
- 题意:给定一个字符串方阵,问对于其中的 8 个方向,是否存在一个指定的字符串
- 思路:很显然的暴力枚举,只不过采用 dfs 进行优化,我们可以发现搜索的逻辑非常的简单,只需要在约束方向的情况下每次遍历八个方向即可。本题的关键在于如何快速正确的编码。对于八个角度判断是否与原始方向一致,我们采用增量的思路,只需要通过传递父结点的位置坐标即可唯一确定,因为两点确定一条了一条射线,方向也就确定了。其次就是如何构造答案矩阵,思路与两点确定射线的逻辑类似,我们在抵达搜索的终点时,只需要通过当前点的坐标与父结点的坐标唯一确定来的路径的方向,进行构造即可
- 时间复杂度:难以计算,但是 dfs 一定可行
1 | |
【dfs】自然数的拆分问题
https://www.luogu.com.cn/problem/P2404
- 题意:给定一个自然数 n,问有多少种拆分方法能将该数拆分为一定数量的升序自然数之和
- 思路:树形搜索的例题。我们采用递增凑数的思路,对于每一个结点值,我们从其父结点的值开始深度搜索,从而确保了和数递增。递归终点就是和值为自然数 n 的值。剪枝就是和值超过了自然数 n 的值
- 时间复杂度:
< < O ( n n ) <<O(n^n)
1 | |
【dfs】Lake Counting S
https://www.luogu.com.cn/problem/P1596
- 题意:给定一个矩阵,计算其中连通块的数量
- 思路:直接逐个元素遍历即可,对于每一个元素,我们采用 dfs 或者 bfs 的方式进行打标签从而将整个连通块都标记出来即可
- 时间复杂度:
O ( n m ) O(nm)
dfs 代码
1 | |
bfs 代码
1 | |
【dfs】填涂颜色
https://www.luogu.com.cn/problem/P1162
- 题意:给定一个方阵,其中只有 0 和 1,其中的 1 将部分的 0 围成了一个圈,现在需要将被围住的 0 转为 2 后,将转化后的方阵输出
- 思路:题意很简单,思路也很显然,我们要做的就是区分开圈内与圈外的 0,如何区分呢?我们采用搜索打标记的方式将外圈的 0 全部打标记之后,遇到的没有打标记的 0 显然就是圈内的了。为了满足所有情况下圈内的 0,我们从方阵的四条边进行探测式打标签即可
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【bfs】马的遍历
https://www.luogu.com.cn/problem/P1443
- 题意:给定一个矩阵棋盘范围与一个马的位置坐标,现在问棋盘中每一个点的最小到达距离是多少
- 思路:很显然的一个 bfs 宽搜模型,我们只需要从该颗马的起始位置开始宽搜,对于每一个第一个搜索到的此前没有到达的点,计算此时到起点的步长距离就是最小到达距离
- 时间复杂度:
O ( n × m ) O(n \times m)
1 | |
【bfs】奇怪的电梯
https://www.luogu.com.cn/problem/P1135
- 题意:给定一个电梯,第
i层只能上升或者下降a[i]层,问从起点开始到终点最少需要乘坐几次电梯- 思路:很显然的一个宽搜,关键在于需要对打标记避免重复访问结点造成死循环
- 时间复杂度:
O ( n ) O(n)
1 | |
【dfs/状压dp】吃奶酪 ⭐
题意:给定一个平面直角坐标系与 n 个点的坐标,起点在坐标原点。问如何选择行进路线使得到达每一个点且总路程最短
思路一:爆搜。题中的
直接无脑爆搜,但是 TLE。爆搜的思路为:每次选择其中的一个点,接下来选择剩余的没有被选择过的点继续搜索,知道所有的点全部都搜到为止 n ≤ 15 n \le 15 时间复杂度:
O ( n ! ) O(n!) 思路二:状态压缩 DP。
时间复杂度:
O ( ) O()
爆搜代码
1 | |
状压 dp 代码
1 | |
【dfs】递归实现指数型枚举
https://www.acwing.com/problem/content/94/
- 题意:给定 n 个数,从其中选择 0-n 个数,将所有的选择方案打印出来,每一个方案中数字按照升序排列
- 思路:很显然的一个二叉树问题。每一个数只有两种状态,选择 or 不选择,于是可以采用二进制枚举 or 二叉树 dfs 的方法进行。为了满足升序,二进制枚举时从低位到高位判断是否为 1 即可;搜索时从低位开始搜索,通过一个动态数组存储搜索路径上的数字即可
- 时间复杂度:
O ( 2 n ) O(2^n)
二进制枚举
1 | |
dfs
1 | |
【dfs】递归实现排列型枚举
https://www.acwing.com/problem/content/96/
- 题意:按照字典序升序,打印 n 个数的所有全排列情况
- 思路:从第一位开始枚举每一位可以选择的数,显然每一位可选择数的数量逐渐减少,直到只有一种选择结束搜索
- 时间复杂度:
O ( n ! ) O(n!)
1 | |
【dfs/树形dp】树的直径 ⭐
树的路径问题,考虑回溯。如何更新值?如何返回值?
参考:https://www.bilibili.com/video/BV17o4y187h1/
【dfs】在带权树网络中统计可连接服务器对数目
题意:给定一棵带权无根树,定义「中转结点」为以当前结点为根,能够寻找到两个不同分支下的结点,使得这两个结点到当前结点的简单路径长度可以被给定值 k 整除,问树中每一个结点的「中转结点」的有效对数是多少
思路:dfs+乘法原理。
- 由于数据量是
,可以直接枚举每一个顶点,并且每一个顶点的操作可以是 n = 1 0 3 n=10^3 的,我们考虑遍历。对于每一个结点,对应的有效对数取决于每一个子树中的简单路径长度合法的结点数,通过深搜统计即可 O ( n ) O(n) - 统计出每一个子树的合法结点后还需要进行答案的计算,也就是有效对数的统计。对于每一个合法结点,都可以和非当前子树上的所有结点结合形成一个合法有效对,直接这样统计会导致结果重复计算一次,因此需要答案除以二。当然也可以利用乘法原理,一边统计每一个子树中有效的结点数,一边和已统计过的有效结点数进行计算
时间复杂度:
O ( n 2 ) O(n^2) 注:总结本题根本原因是提升对建图的理解以及针对
vector用法的总结
- 关于建图
- 一开始编码时,我设置了结点访问状态数组
vector<bool> vis和每一个结点到当前根结点的距离数组vector<int> d,但其实都可以规避,因为本题是「树」形图,可以通过在深搜时同时传递父结点来规避掉vis数组的使用- 同时由于只需要在遍历时计算路径是否合法从而计数,因此不需要存储每一个结点到当前根结点的路径值,可以通过再增加一个搜索状态参数来规避掉
d数组的使用- 关于
vector
- 一开始使用了全局
vis数组,因此每次都需要进行清空操作。我使用了.clear()方法试图重新初始化数组,但这导致了状态的错误记录,可能是 LeetCode 平台 C++ 语言特有的坑,还是少用全局变量.clear()方法会导致.size()为 0,但是仍然可以通过[]方法获得合法范围内的元素值,这是vector内存分配优化的结果
1 | |
1 | |
【dfs】将石头分散到网格图的最少移动次数
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/
标签:搜索、全排列、库函数
题意:给定一个
的矩阵 3 × 3 3\times 3 ,其中数字总和为 9 且 g g ,现在需要将其中 g [ i ] [ j ] ≥ 0 g[i][j] \ge 0 的数字逐个移动到值为 0 的位置上使得最终矩阵全为 1,问最少移动长度是多少。 > 1 >1 思路一:手写全排列
- 思路:可以将这道题抽象为求解「将 a 个大于 1 位置的数分配到 b 个 0 位置」的方案中的最小代价问题。容易联想到全排列选数的母问题:数字的位数对应这里的 b 个 0 位置,每个位置可以填的数对应这里的用哪个 a 来填。区别在于:0 的位置顺序不是固定的,用哪个 a 来填的顺序也不是固定的。这与全排列数中:被填的位置顺序是固定的,用哪个数来填不是固定的,有所区别。因此我们可以全排列枚举每一个位置,在此基础之上再全排列枚举每一个位置上可选的 a 进行填充。可以理解为全排列的嵌套。那么最终递归树的深度就是 0 的个数,递归时再用一个参数记录每一个选数分支对应的代价即可。
- 时间复杂度:
O ( 9 × 9 ! ) O(9\times 9!) 思路二:库函数全排列
- 思路:由于方阵的总和为 9,因此 >1 的位置上减去 1 剩下的数值之和一定等于方阵中 0 的个数。因此我们可以将前者展开为和 0 相同大小的向量,并全排列枚举任意一者进行两者的匹配计算,维护其中的最小代价即是答案。
- C++ 的全排列枚举库函数为
std::next_permutation(ItFirst, ItEnd)- Python 的全排列枚举库函数为
itertools.permutations(Iterable)- 时间复杂度:
O ( 9 × 9 ! ) O(9\times 9!)
1 | |
1 | |
1 | |
1 | |
数据结构由 数据 和 结构 两部分组成。我们主要讨论的是后者,即结构部分。
按照 逻辑结构 可以将其区分为 线性结构 和 非线性结构。
按照 物理结构 可以将其区分为 连续结构 和 分散结构。
【模板】双链表
https://www.acwing.com/problem/content/829/
思路:用两个空结点作为起始状态的边界,避免所有边界讨论。
时间复杂度:插入、删除结点均为
,遍历为 O ( 1 ) O(1) O ( n ) O(n)
1 | |
1 | |
【模板】单调栈
https://www.acwing.com/problem/content/832/
题意:对于一个序列中的每一个元素,寻找每一个元素左侧最近的比其小的元素。
思路一:暴力枚举
- 显然对于每一个元素
nums[i],我们可以枚举倒序[0, i-1]直到找到第一个nums[j] < nums[i]- 时间复杂度:
O ( n 2 ) O(n^2) 思路二:单调栈
可以发现时间开销主要在倒序枚举上,我们能少枚举一些元素吗?答案是可以的。我们定义「寻找
[i-1, 0]中比当前元素小的第一个元素」的行为叫做「寻找合法对象」。显然我们在枚举每一个元素时都需要 查询 和 维护 这样的合法对象线性序列,可以理解为记忆化从而加速查询。那么如何高效查询和维护这样的线性序列呢?不妨考虑每一个合法对象对曾经的合法对象的影响:
- 若当前元素
nums[i]可以成为后续[i+1, n-1]元素的合法对象。则从i-1开始一直往左,只要比当前大的元素,都不可能成为[i+1, n-1]的合法对象,肯定都被nums[i]“拦住了”。那么在「合法对象序列」中插入当前合法对象之前,需要不断尾弹出比当前大的元素- 若当前元素
nums[i]不能成为后续[i+1, n-1]元素的合法对象。表明当前元素过大,此时就不用将当前元素插入「合法对象序列」经过上述两个角度的讨论,很容易发现这样维护出来的的合法序列是严格单调递增的。于是,在查询操作时仅需要进行尾比较与尾弹出即可,在维护操作时,仅需要尾插入即可。满足这样的线性数据结构有很多,如栈、队列、数组、链表,我们就使用栈来演示,与标题遥相呼应
时间复杂度:
O ( n ) O(n)
1 | |
相似题:
【模板】单调队列
标签:双端队列、滑动窗口、单调队列
题意:给定一个含有 n 个元素的序列,求解其中每个长度为 k 的子数组中的最值。
思路:显然我们可以
暴力求解,有没有什么方法可以将「求解子数组中最值」的时间开销从 O ( n k ) O(nk) 降低为 O ( k ) O(k) 呢?有的!我们重新定义一个队列就好了。为了做到线性时间复杂度的优化,我们对队列做以下自定义,以「求解子数组最小值」为例: O ( 1 ) O(1)
- 插入元素到队尾:此时和单调栈的逻辑类似。如果当前元素可以作为当前子数组或后续子数组的最小值,则需要从当前队尾开始依次弹出比当前元素严格大的元素,最后再将当前元素入队。注意:当遇到和当前元素值相等的元素时不能出队,因为每一个元素都会经历入队和出队的操作,一旦此时出队了,后续进行出队判定时会提前弹出本不应该出队的与其等值的元素。
- 弹出队头元素:如果队头元素和子数组左端点
nums[i-k]的元素值相等,则弹出。- 获得队头元素:
的获取队头元素,即队列中的最小值。 O ( 1 ) O(1) 时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【模板】最近公共祖先
https://www.luogu.com.cn/problem/P3379
题意:寻找树中指定两个结点的最近公共祖先
。 (Lowest Common Ancestor, 简称 LCA) \text{(Lowest Common Ancestor, 简称 LCA)} 思路:对于每次查询,我们可以从指定的两个结点开始往上跳,第一个公共结点就是目标的 LCA,每一次询问的时间复杂度均为
,为了加速查询,我们可以采用倍增法,预处理出往上跳的结果,即 O ( n ) O(n) fa[i][j]数组,表示号点向上跳 i i 步后到达的结点。接下来在往上跳跃的过程中,利用二进制拼凑的思路,即可在 2 j 2^j 的时间内查询到 LCA。 O ( log n ) O(\log n) 预处理:可以发现,对于
fa[i][j],我们可以通过递推的方式获得,即fa[i][j] = fa[fa[i][j-1]][j-1],当前结点向上跳跃步可以拆分为先向上 2 j 2^j 步, 在此基础之上再向上 2 j − 1 2^{j-1} 步.于是我们可以采用宽搜 2 j − 1 2^{j-1} 深搜的顺序维护 o r or 数组。 f a fa 跳跃:我们首先需要将两个结点按照倍增的思路向上跳到同一个深度,接下来两个结点同时按照倍增的思路向上跳跃,为了确保求出最近的,我们需要确保在跳跃的步调一致的情况下,两者的祖先始终不相同,那么倍增结束后,两者的父结点就是最近公共祖先,即
fa[x][k]或fa[y][k]时间复杂度:
Θ ( n log n + m log n ) \Theta(n \log n + m \log n)
为预处理每一个结点向上跳跃抵达的情况 n log n n \log n 为 m log n m \log n 次询问的情况 m m
1 | |
【栈】验证栈序列
https://www.luogu.com.cn/problem/P4387
题意:给定入栈序列与出栈序列,问出栈序列是否合法
思路:思路很简单,就是对于当前出栈的数,和入栈序列中最后已出栈的数之间,如果还有数没有出,那么就是不合法的出栈序列,反之合法。这是从入栈的结果来看的,如果这么判断就需要扫描入栈序列 n 次,时间复杂度为
。我们按照入栈的顺序来看,对于当前待入栈的数,若与出栈序列的队头不等,则成功入栈等待后续出栈;若与出栈序列相等,则匹配成功直接出栈无需入栈,同时对已入栈的数与出栈序列队头不断匹配直到不相等。最后判断待入栈的数与出栈序列是否全部匹配掉了,如果全部匹配掉了说明该出栈序列合法,反之不合法 O ( n 2 ) O(n^2) 抽象总结上述思路:为了判断出栈序列是否合法,我们不妨思考:对于每一个出栈的数,出栈的时机是什么?可以发现出栈的时机无非两种:
- 一入栈就出栈(对应于枚举待入栈序列时发现待入栈的数与出栈序列队头相等)
- 紧跟着刚出栈的数继续出栈(对应于枚举待入栈序列时发现待入栈的数与出栈序列队头相等之后,继续判断出栈序列队头与已入栈的数是否相等,若相等则不断判断并出栈)
时间复杂度:
O ( n ) O(n)
1 | |
二叉搜索树 & 平衡树
如果我们想要在
关于平衡二叉搜索树,有非常多的变种与实现,不同的应用场景会选择不同的平衡树类型。Treap 更灵活,通过随机化优先级实现预期的平衡,但在最坏情况下可能退化。AVL 树 严格保持平衡,保证了 map 和 set)。一般来说,红黑树是一个较为通用的选择,而在需要严格平衡性时,AVL 树可能是更好的选择。
Treap
Treap 是二叉搜索树和堆的结合体。它通过维护两种性质来保持平衡:
- 二叉搜索树性质:每个节点的左子树的所有节点值小于该节点的值,右子树的所有节点值大于该节点的值。
- 堆性质:每个节点的优先级(通常随机生成)要大于或等于其子节点的优先级。
平衡机制:
- Treap 使用随机化优先级使得树的形状接近于理想的平衡树(期望树高为
)。 O ( log n ) O(\log n) - 通过旋转操作(左旋和右旋)在插入和删除时保持堆的性质。
优点:
- 实现相对简单。
- 由于随机化的优先级,在期望情况下,树的高度是
。 O ( log n ) O(\log n) - 灵活性高,可以根据需要调整优先级函数。
缺点:
- 最坏情况下,树的高度可能退化为
(例如所有优先级相同或顺序生成的优先级),尽管发生概率很低。 O ( n ) O(n)
AVL 树
AVL 树是最早发明的自平衡二叉搜索树之一,1962 年由 Adelson-Velsky 和 Landis 发明。
- 平衡因子:每个节点的左右子树高度差不能超过
,且需要记录每个节点的高度。 1 1 平衡机制:
- 插入或删除节点后,如果某个节点的平衡因子不再为
、 − 1 -1 或 0 0 ,就需要通过旋转(单旋转或双旋转)来恢复平衡。 1 1 - 旋转操作包括:左旋转、右旋转、左右双旋转和右左双旋转。
优点:
- 严格的平衡条件保证了树的高度始终为
,因此搜索、插入和删除操作的时间复杂度为 O ( log n ) O(\log n) 。 O ( log n ) O(\log n) 缺点:
- 由于平衡条件严格,每次插入和删除后可能需要较多的旋转操作,从而导致实现较复杂,插入和删除操作的常数时间开销较大。
红黑树
红黑树是一种较为宽松的自平衡二叉搜索树,由 Rudolf Bayer 于 1972 年发明。
- 颜色属性:每个节点都有红色或黑色两种颜色,通过这些颜色约束树的平衡性。
平衡机制:
- 通过遵循红黑树的五个性质来保持平衡:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 叶子节点(NIL 节点)是黑色。
- 如果一个节点是红色的,那么它的子节点必须是黑色(红节点不能连续出现)。
- 从任一节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。
- 插入和删除操作可能破坏红黑树的性质,需要通过重新着色和旋转来恢复平衡。
优点:
- 红黑树的高度最多是
,因此搜索、插入和删除操作的时间复杂度仍为 Θ ( 2 log n ) \Theta (2 \log n) 。 O ( log n ) O(\log n) - 由于平衡条件较为宽松,插入和删除操作需要的旋转操作通常比 AVL 树少,效率更高。
缺点:
- 实现较复杂,特别是插入和删除的平衡修复过程。
- 虽然红黑树的搜索效率与 AVL 树相似,但由于平衡条件较宽松,实际应用中的树高度通常略高于 AVL 树,因此搜索操作的效率稍低。
【二叉树】美国血统
https://www.luogu.com.cn/problem/P1827
题意:给定二叉树的中序和先序序列,输出后序序列
思路:经典二叉树的题目,主要用于巩固加强对于递归的理解。指针其实是没有必要的,为了得到后序序列,我们只需要有一个 dfs 序即可,为了得到 dfs 序,我们只需要根据给出的中序和前序序列即可得到 dfs 序
时间复杂度:
O ( n ) O(n)
指针做法
1 | |
构造出 dfs 序直接输出
1 | |
【二叉树】新二叉树
https://www.luogu.com.cn/problem/P1305
题意:给定一棵二叉树的 n 个结点信息,分别为当前结点的数据信息、左孩子结点信息和右结点信息,输出这棵二叉树的前序序列
思路:我们首先将这棵二叉树构建出来,接着遍历输出前序序列即可。关键在于如何构建二叉树?我们使用数组存储二叉树,对于每一个树上结点,我们将数组中元素的索引存储为树上结点信息,每一个结点再存储左孩子与右孩子的信息
时间复杂度:
O ( n ) O(n)
1 | |
【二叉树】遍历问题
https://www.luogu.com.cn/problem/P1229
题意:给定一棵二叉树的前序序列与后序序列,问中序序列的可能情况有多少种
思路:我们采用从最小结构单元的思路进行考虑,即假设当前二叉树只有一个根结点与两个叶子结点,而非两棵子树。然后将题意进行等价变换,即问对于已经固定的前序和后序二叉树,该二叉树有多少种不同的形状?对于当前的最小结构二叉树,形状就是 左右根 or 根左右,现在的根可以直接确定,那么就只能从左右孩子进行变形,很显然只能进行左右交换的变形,但是问题是一旦左右变换,前序 or 后序都会变掉,说明这种左右孩子都存在的前后序固定的二叉树是唯一的,那么如何才是不唯一的呢?我们考虑减少孩子数量。假设没有孩子,那么很显然也只有一个形状,就是一个根结点,故排除。于是答案就呼之欲出了,就是当根结点只有一个孩子时,这个孩子无论是在左边还是右边,前后序都是相同的,但是中序序列就不同了,于是就产生了两种中序序列。于是最终的结论是:对于前后序确定的二叉树来说,中序序列的情况是就是
个。现在的问题就转变为了在给定前后序的二叉树中求解单分支结点个数的问题。 2 单分支结点数 2^{\text{单分支结点数}} 如何寻找单分支结点呢?根据下面的递归图可以发现,无论是左单分支还是右单分支,如果 pre 的连续两个结点与 post 的连续两个结点对称相同,那么就一定有一个单分支结点,故只需要寻找前后序序列中连续两个字符对称相同的情况数 cnt 即可。最终的答案数就是
2 c n t 2^{cnt}
时间复杂度:
O ( n m ) O(nm)
1 | |
【二叉树】医院设置 🔥
https://www.luogu.com.cn/problem/P1364
题意:给定一棵二叉树,树中每一个结点存储了一个数值表示一个医院的人数,现在需要在所有的结点中将一个结点设置为医院使得其余结点中的所有人到达该医院走的路总和最小。路程为结点到医院的最短路,边权均为 1。给出最终的最短路径总和
思路一:暴力
显然的对于已经设置好医院的局面,需要求解的路径总和就直接将树遍历一边即可。每一个结点都可以作为医院进行枚举,每次遍历是
的 O ( n ) O(n) 时间复杂度:
O ( n 2 ) O(n^2) 思路二:带权树的重心
- TODO
- 时间复杂度:
O ( n ) O(n)
暴力代码
1 | |
优化代码
1 | |
【二叉树】二叉树深度
https://www.luogu.com.cn/problem/P4913
题意:给定一棵二叉树,求解这棵二叉树的深度
思路:有两个考点,一个是如何根据给定的信息(从根结点开始依次给出已存在树上结点的左右孩子的编号)构建二叉树,一个是如何求解已经构建好的二叉树的深度。对于构建二叉树,我们沿用 T5 数组模拟构建的思路,直接定义结点类型即可;对于求解深度,很显然的一个递归求解,即左右子树深度值 +1 即可
时间复杂度:
O ( n ) O(n)
1 | |
【完全二叉树】淘汰赛
https://www.luogu.com.cn/problem/P1364
题意:给定
支球队的编号与能力值,进行淘汰赛,能力值者晋级下一轮直到赛出冠军。输出亚军编号 2 n 2^n 思路:很显然的一个完全二叉树的题目。我们都不需要进行递归操作,直接利用完全二叉树的下标性质利用数组模拟循环计算即可。给出的信息就是完全二叉树的全部叶子结点的信息,分别为球队编号 id 与球队能力值 val,我们从第 n-1 个结点开始循环枚举到第 1 个结点计算每一轮的胜者信息,最终输出最后一场的能力值较小者球队编号即可
时间复杂度:
Θ ( 2 n ) \Theta(2n)
1 | |
【二叉树/LCA】二叉树问题
https://www.luogu.com.cn/problem/P3884
题意:给定一棵二叉树的结点关系信息,求出这棵二叉树的深度、宽度和两个指定结点之间的最短路径长度
思路:二叉树的构建直接采用有向图的构造方法。深度直接 dfs 即可,宽度直接在 dfs 遍历时哈希深度值即可。问题的关键在于如何求解两个给定结点之间的路径长度,很显然需要求解两个结点的 LCA,由于结点数
故直接采用暴力的方法,可以重定义结点,增加父结点域。也可以通过比对根结点到两个指定结点的路径信息得到 LCA 即最后一个相同的结点编号(本题采用),通过在 dfs 遍历树时存储路径即可得到根结点到两个指定结点的路径信息。之后直接根据题中新定义的路径长度输出即可,即 ≤ 100 \le 100
length = 2 × ( d x − d l c a ) + ( d y − d l c a ) \text{length} = 2 \times (d_x - d_{lca}) + (d_y - d_{lca}) 其中
表示:根结点到第 d i d_i 号点之间的路径长度,在 dfs 时通过传递深度值维护得到 i i 时间复杂度:
O ( n ) O(n)
1 | |
【set】营业额统计
https://www.luogu.com.cn/problem/P2234
题意:给定一个序列 a,需要计算
,即计算每一个数与序列中当前数之前的数的最小差值之和 a 1 + ∑ i = 2 , 1 ≤ j < i n min ∣ a i − a j ∣ a_1 + \displaystyle \sum_{i=2,1 \le j <i}^{n} \min {|a_i - a_j|} 思路:很显然的思路,对于每一个数,我们需要对之前的序列在短时间内找到一个数值最接近当前数的数。
- TLE:一开始的思路是每次对之前的序列进行排序,然后二分查找与当前值匹配的数,为了确保所有的情况都找到,就直接判断二分查到的数,查到的数之前的一个数,之后的一个数,但是时间复杂度极高(我居然没想到),是
O ( n 2 log n ) O(n^2 \log n) - AC:后来看了题解才知道
set的正确用法,就是一个 平衡树的 STL。我们对于之前的序列不断的插入平衡树中(默认升序排序),每次利用s.lower_bound(x)返回「集合s中第一个当前数的迭代器」,然后进行判断即可。 ≥ \ge lower_bound()的时间复杂度为。需要注意的是边界的判断,一开始的思路虽然会超时,但是二分后边界的判断很简单,使用 STL 后同样需要考虑边界的情况。分为三种(详情见代码) O ( log n ) O(\log n)
- 当前数比集合中所有的数都大,那么
lower_bound就会返回s.end()答案就是当前数与集合中最后一个数的差值- 当前数比集合中所有的数都小,那么
lower_bound就会返回s.bigin()答案就是集合中第一个数与当前数的差值- 当前数存在于集合中 or 集合中既有比当前数大的又有比当前数小的,那么就比较查到的数与查到的数前一个数和当前数的差值,取最小的差值即可
时间复杂度:
O ( n log n ) O(n \log n)
TLE 但逻辑清晰代码
1 | |
AC 的 set 代码
1 | |
【multiset】切蛋糕
https://www.acwing.com/problem/content/description/5581/
题意:给定一个矩形,由左下角和右上角的坐标确定。现在对这个矩形进行切割操作,要么竖着切,要么横着切。现在需要给出每次切割后最大子矩形的面积
思路:STL set。很容易想到,横纵坐标是相互独立的,最大子矩形面积一定产生于最大长度与最大宽度的乘积。因此我们只需要维护一个序列的最大值即可。对于二维可以直接当做一维来看,于是问题就变成了,需要在
的时间复杂度内,对一个序列完成下面三个操作: log n \log n
- 删除一个数
- 增加一个数(执行两次)
- 获取最大值
如何实现呢?我们需要有序记录每一个子线段的长度,并且子线段的长度可能重复,因此我们用
std::multiset来存储所有子线段的长度
- 使用
M.erase(M.find(value))实现:删除一个子线段长度值- 使用
M.insert(value)实现:增加子线段一个长度值- 使用
*M.rbegin()实现:获取当前所有子线段长度的最大值由于给的是切割的位置坐标
x,因此上述操作 1 不能直接实现,我们需要利用给定的切割坐标x计算出当前切割位置对应子线段的长度。如何实现呢?我们知道,对于当前切割的坐标x,对应的子线段的长度取决于当前切割坐标左右两个切割的位置rp, lp,因此我们只需要存储每一个切割的坐标即可。由于切割位置不会重复,并且需要在的时间复杂度内查询到,因此我们还是可以使用 log n \log n std::set来存储切割位置时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【并查集】Milk Visits S
https://www.luogu.com.cn/problem/P5836
题意:给定一棵树,结点被标记成两种,一种是 H,一种是 G,在每一次查询中,需要知道指定的两个结点之间是否含有某一种标记
思路:对于树上标记,我们可以将相同颜色的分支连成一个连通块
- 如果查询的两个结点在同一个连通块,则查询两个结点所在的颜色与所需的颜色是否匹配即可
- 如果查询的两个结点不在同一个连通块,两个结点之间的路径一定是覆盖了两种颜色的标记,则答案一定是 1
时间复杂度:
Θ ( n + m ) \Theta(n+m)
1 | |
【并查集】尽量减少恶意软件的传播
https://leetcode.cn/problems/minimize-malware-spread/description/
题意:给定一个由邻接矩阵存储的无向图,其中某些结点具备感染能力,可以感染相连的所有结点,问消除哪一个结点的感染能力可以使得最终不被感染的结点数量尽可能少,给出消除的有感染能力的最小结点编号
思路:很显然我们可以将当前无向图的多个连通分量,共三种感染情况:
如果一个连通分量中含有
个感染结点,则当前连通分量一定会被全部感染; ≥ 2 \ge 2 如果一个连通块中含有
个感染结点,则无需任何操作; 0 0 如果一个连通块中含有
个感染结点,则最佳实践就是移除该连通块中唯一的那个感染结点。 1 1 当然了,由于只能移走一个感染结点,我们需要从所有只含有
个感染结点的连通块中移走连通块结点最多的那个感染结点。因此我们需要统计每一个连通分量中感染结点的数量以及总结点数,采用并查集进行统计。需要注意的是题目中的“索引最小”指的是结点编号最小而非结点在序列 1 1 中的下标最小。算法流程见代码。 i n i t i a l initial 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【并查集】账户合并
https://leetcode.cn/problems/accounts-merge/
题意:给定 n 个账户,每一个账户含有一个用户名和最多 m 个绑定的邮箱。由于一个用户可能注册多个账户,因此我们需要对所有的账户进行合并使得一个用户对应一个账户。合并的规则是将所有「含有相同邮箱的账户」视作同一个用户注册的账户。返回合并后的账户列表。
思路:这道题的需求很显然,我们需要合并含有相同邮箱的账户。显然有一个暴力的做法,我们直接枚举每一个账户中所有的邮箱,接着枚举剩余账户中的邮箱进行匹配,匹配上就进行合并,但这样做显然会造成大量的冗余匹配和冗余合并,我们不妨将这两个过程进行拆分。我们需要解决两个问题:
- 哪些账户需要合并?很容易想到并查集这样的数据结构。我们使用哈希表存储每一个邮箱的账户编号,最后进行集合合并即可维护好每一个账号归属的集合编号。
O ( n m ) O(nm) - 如何合并指定账户?对于上述维护好的集合编号,我们需要合并所有含有相同“祖先”的账户。排序去重或使用有序列表均可实现。
O ( n log n ) O(n\log n) 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
1 | |
【树状数组】将元素分配到两个数组中 II
https://leetcode.cn/problems/distribute-elements-into-two-arrays-ii/description/
题意:给定
个数,现在需要将这些数按照某种规则分配到两个数组 n n 和 A A 中。初始化分配 B B nums[0]到中, A A nums[1]到中,接下来对于剩余的每个元素 B B nums[i],分配取决于和 A A 中比当前元素 B B nums[i]大的个数,最终返回两个分配好的数组思路:首先每一个元素都需要进行枚举,那么本题需要考虑的就是如何在
时间复杂度内统计出两数组中比当前元素大的元素个数。针对 C++ 和 Python 分别讨论 log \log
- C++
- 法一:
std::multiset<int>。可惜不行,因为统计比当前元素大的个数时,s.rbegin() - s.upper_bound(nums[i])是不合法的,因为std::multiset<int>的迭代器不是基于指针的,因此无法直接进行加减来计算地址差,遂作罢- 法二:树状数组。很容易想到利用前缀和统计比当前数大的数字个数,但是由于此处需要对前缀和进行单点修改,因此时间复杂度肯定会寄。有什么数据结构支持「单点修改,区间更新」呢?我们引入树状数组。我们将数组元素哈希到
[1, len(set(nums))]区间,定义哈希后的当前元素nums[i]为x,对于当前哈希后的x而言想要知道两个数组中有多少数比当前数严格大,只需要计算前缀和数组arr中arr[n] - arr[x]的结果即可- Python
SortedList。python 有一个sortedcontainers包其中有SortedList模块,可以实现std::multiset<int>所有操作并且可以进行随机下标访问,于是就可以进行下标访问 log \log 计算比当前数大的元素个数 O ( 1 ) O(1) - 题外话。LeetCode 可以进行第三方库导入的操作,某些比赛不允许,需要手搓
SortedList模块,当然可以用树状数组 or 线段树解决,板子链接:https://blog.dwj601.cn/Algorithm/a_template/#SortedList时间复杂度:
O ( n log n ) O(n \log n)
1 | |
1 | |
1 | |
【线段树/二分】以组为单位订音乐会的门票 🔥
https://leetcode.cn/problems/booking-concert-tickets-in-groups/
题意:给定一个长为
且初始值均为 n ≤ 5 × 1 0 4 n\le 5 \times 10^4 的数组 0 0 ,数组中的每个元素最多增加到 a a 。现在需要以这个数组为基础进行 m m 次询问,每次询问是以下两者之一: q ≤ 5 × 1 0 4 q\le 5 \times 10^4
- 给定一个
和 k k ,找到最小的 l i m lim 使得 i ∈ [ 0 , l i m ] i \in [0,lim] m − a i ≥ k m - a_i \ge k - 给定一个
和 k k ,找到最小的 l i m lim 使得 i ∈ [ 0 , l i m ] i \in [0,lim] m × ( i + 1 ) − ∑ j = 0 i a j ≥ k \displaystyle m\times (i+1) - \sum_{j=0}^i a_j \ge k 思路一:暴力。对于询问 1,我们直接顺序遍历 a 数组直到找到第一个符合条件的即可;对于询问 2,同样直接顺序遍历 a 数组直到找到第一个符合条件的即可。时间复杂度为
。 O ( q n ) O(qn) 思路二:线段树上二分。
暴力代码:
1 | |
线段树上二分代码:
1 | |
将大问题转化为等价小问题进行求解。
【分治】随机排列
https://www.acwing.com/problem/content/5469/
题意:给定一个 n 个数的全排列序列,并将其进行一定的对换,问是对换了 3n 次还是 7n+1 次
思路:可以发现对于两种情况,就对应对换次数的奇偶性。当 n 为奇数:3n 为奇数,7n+1 为偶数;当 n 为偶数:3n 为偶数,7n+1 为奇数。故我们只需要判断序列的逆序数即可。为了求解逆序数,我们可以采用归并排序的 combine 过程进行统计即可
时间复杂度:
O ( n log n ) O(n \log n)
1 | |
无论是深搜还是宽搜,都逃不掉图的思维。我们将搜索图建立起来之后,剩余的编码过程就会跃然纸上。
【dfs】机器人的运动范围
https://www.acwing.com/problem/content/22/
1 | |
【dfs】CCC单词搜索
https://www.acwing.com/problem/content/5168/
搜索逻辑:分为正十字与斜十字
更新答案逻辑:需要进行两个条件的约数,一个是是否匹配到了最后一个字母,一个是转弯次数不超过一次
转弯判断逻辑:
首先不能是起点开始的
对于正十字:如果next的行 & 列都与pre的行和列不相等,就算转弯
对于斜十字:如果next的行 | 列有和pre相等的,就算转弯
1 | |
【dfs/二进制枚举】数量
https://www.acwing.com/problem/content/5150/
题意:给定一个数n,问[1, n]中有多少个数只含有4或7
思路一:dfs
- 对于一个数,我们可以构造一个二叉搜数进行搜索,因为每一位只有两种可能,那么从最高位开始搜索。如果当前数超过了n就return,否则就算一个答案
- 时间复杂度:
Θ ( 2 1 + lg ( max ( a [ i ] ) ) ) \Theta(2^{1 + \lg{(\max(a[i])})}) 思路二:二进制枚举
- 按照数位进行计算。对于一个 x 位的数,1 到 x-1 位的情况下所有的数都符合条件,对于一个 t 位的数,满情况就是
种,所以 2 t 2^t [1,x-1]位就一共有种情况 。对于第 x 位,采取二进制枚举与原数进行比较,如果小于原数,则答案 +1,反之结束循环输出答案即可 2 1 + 2 2 + ⋯ + 2 x − 1 = 2 x − 2 2^1 + 2^2 + \cdots + 2^{x - 1} = 2^{x} - 2
dfs 代码:
1 | |
二进制枚举代码:
1 | |
【dfs】组合总和
https://leetcode.cn/problems/combination-sum/
题意:给定一个序列,其中的元素没有重复,问如何选取其中的元素,使得选出的数字总和为指定的数字target,选取的数字可以重复
思路:思路比较简答,很容易想到用dfs搜索出所有的组合情况,即对于每一个“结点”,我们直接遍历序列中的元素即可。但是由于题目的限制,即不允许合法的序列经过排序后相等。那么为了解决这个约束,我们可以将最终搜索到的序列排序后进行去重,但是这样的时间复杂度会很高,于是我们从搜索的过程切入。观看这一篇题解 防止出现重复序列的启蒙题解,我们提取其中最关键的一个图解
可见3,4和4,3的剩余选项(其中可能包含了答案序列)全部重复,因此我们直接减去这个枝即可。不难发现,我们根据上述优化思想,剪枝的操作可以为:让当前序列开始枚举的下标
idx从上一层开始的下标i开始,于是剪枝就可以实现了。时间复杂度:
Θ ( 2 n log n ) \Theta \left ( 2^{\frac{n}{\log n}}\right)
1 | |
【递归】扩展字符串
https://www.acwing.com/problem/content/5284/
题意:给定一种字符串的构造方式,问构造n次以后的字符串中的第k个字符是什么
思路:由于构造的方法是基于上一种情况的,很容易可以想到一个递归搜索树来解决。只是这道题有好几个坑,故记录一下。
- 首先说一下搜索的思路:对于当前的状态,我们想要知道第k个位置上的字符,很显然我们可以通过预处理每一种构造状态下的字符串长度得到下一个字符串的长度,于是我们可以在当前的字符串中,通过比对下标与五段字符串长度的大小,来确定是继续递归还是直接输出
- 特判:可以发现,对于
的情况,我们无法采用相同的结构进行计算,故进行特判,如果当前来到了最初始的字符串状态,我们直接输出相应位置上的字符即可 n = 0 n=0 - 最后说一下递归终点的设计:与搜索所有的答案情况不同,这道题的答案是唯一的,因此我们在搜索到答案后,可以通过一个
bool变量作为一个标记,表示已经找到答案了,只需要不断回溯直到回溯结束为止,就不需要再遍历其他的分支了- **坑:**这道题的坑说实话有点难崩。
- 首先是一个k的大小,是一定要开
long long的,我一开始直接全局宏定义int为long long了- 还有一个坑可能是只要我才会犯的,就是字符串按照下标输出字符的时候,是需要
-1的,闹心的是我有的加了,有的没加,还是debug的时候调出来的- 最后一个大坑,属于是引以为戒了。就是这句
len[i] = min(len[i], (int)2e18),因为我们可以发现,抛开那三个固定长度的字符串来说,每一次新构造出来的字符串长度都是上一个字符串长度倍,那么构造 2 2 次后的字符串长度就是 n n 长度的 s 0 s_0 倍,那么对于 2 n 2^n 的取值范围来说,直接存储长度肯定是不可取的。那么如何解决这个问题呢?方法是我们对 n n len[i]进行一个约束即可,见代码。最后进行递归比较长度就没问题了。- 时间复杂度:
- 由于每一个构造的状态我们都是常数级别的比较,因此相当于一个状态的搜索时间复杂度为 O ( n ) O(n) ,那么总合就是 O ( 1 ) O(1) O ( n ) O(n)
1 | |
【dfs】让我们异或吧
https://www.luogu.com.cn/problem/P2420
题意:给定一棵树,树上每一条边都有一个权值,现在有Q次询问,对于每次询问会给出两个结点编号u,v,需要输出结点u到结点v所经过的路径的所有边权的异或之和
思路:对于每次询问,我们当然可以遍历从根到两个结点的所有边权,然后全部异或计算结果,但是时间复杂度是
,显然不行,那么有什么优化策略吗?答案是有的。我们可以发现,对于两个结点之间的所有边权,其实就是根到两个结点的边权相异或得到的结果(异或的性质),我们只需要预处理出根结点到所有结点的边权已异或值,后续询问的时候直接 O ( n ) O(n) 计算即可 O ( 1 ) O(1) 时间复杂度:
Θ ( n + q ) \Theta(n+q)
1 | |
【记忆化搜索】Function
https://www.luogu.com.cn/problem/P1464
题意:
思路一:直接dfs
- 直接按照题意进行dfs代码的编写,但是很显然时间复杂极高
- 时间复杂度:
O ( T × 情况数 ) O(T \times \text{情况数}) 思路二:记忆化dfs
- 记忆化逻辑:
- 如果当前的状态没有记忆过,就记忆一下
- 如果当前的状态已经记忆过了,就不需要继续递归搜索了,直接使用之前已经记忆过的答案即可
- 上述起始状态需要和搜到答案的状态做一个区别。我们知道,对于一组合法的输入,答案一定是
- 注意点:
- 输入终止条件不是
a != -1 && b != -1 && c != -1,而是要三者都不是-1才行- 对于每一组输入,我们不需要
memset记忆数组,因为每一组的记忆依赖是相同的- 由于答案一定是
的,因此是否记忆过只需要看当前状态的答案是否 > 0 >0 即可 > 0 >0 - 时间复杂度:
< O ( T × n 3 ) <O(T \times n^3)
直接dfs代码:
1 | |
记忆化dfs代码:
1 | |
【递归】外星密码
https://www.luogu.com.cn/problem/P1928
线性递归
题意:给定一个压缩后的密码串,需要解压为原来的形式。压缩形式距离
AC[3FUN]→ \to ACFUNFUNFUNAB[2[2GH]]OP→ \to ABGHGHGHGHOP思路:
我们采用递归的策略
我们知道,对于每一个字符,一共有4种情况,分别是:“字母”、“数字”、“[”、“]”。如果是字母。我们分情况考虑
- “字母”:
- 直接加入答案字符串即可
- “[”:
- 获取左括号后面的整体 - 采用递归策略获取后面的整体
- 加入答案字符串
- “数字”:
- 获取完整的数 - 循环小trick
- 获取数字后面的整体 - 采用递归策略获取后面的整体
- 加入答案字符串 - 循环尾加入即可
- 返回当前的答案字符串
- “]”:
- 返回当前的答案字符串 - 与上述 “[” 对应
代码设计分析:
我们将压缩后的字符串看成由下面两种单元组成:
- 最外层中括号组成的单元:如
[2[2AB]]就算一个最外层中括号组成的单元- 连续的字母单元:如
OPQ就算一个连续的字母单元解决各单元连接问题:
为了在递归处理完第一种单元后还能继续处理后续的第二种单元,我们直接按照压缩字符串的长度进行遍历,即
while (i < s.size())操作解决两种单元内部问题:
- 最外层中括号组成的单元:递归处理
- 连续的字母单元:直接加入当前答案字符串即可
手玩样例:
- 显然按照定义,上述压缩字符串一共有五个单元
- 我们用红色表示进入递归,蓝色表示驱动递归结束并回溯。可以发现
时间复杂度:
Θ ( res.length() ) \Theta(\text{res.length()})
1 | |
【dfs+剪枝/二进制枚举】选数
https://www.luogu.com.cn/problem/P1036
题意:给定n个数,从中选出k个数,问一共有多少种方案可以使得选出来的k个数之和为质数
思路一:dfs+剪枝
- 按照数据量可以直接暴搜,搜索依据是每一个数有两种状态,即选和不选,于是搜索树就是一棵二叉树
- 搜索状态定义为:对于当前第idx个数,已经选择了cnt个数,已经选择的数之和为sum
- 搜索终止条件为:idx越界
- 剪枝:已经选择了k个数就直接返回,不用再选剩下的数了
- 时间复杂度:
- 剪枝后一定是小于这个复杂度的 O ( 2 n ) O(2^n) 思路二:二进制枚举
- 直接枚举
,按照其中含有的 0 → 2 n − 1 0\to 2^n-1 的个数,来进行选数判断 1 1 - 时间复杂度:
- 一定会跑满的 O ( 2 n ) O(2^n)
dfs+剪枝
1 | |
二进制枚举
1 | |
【dfs/bfs】01迷宫
https://www.luogu.com.cn/problem/P1141
题意:给定一个01矩阵,行走规则为“可以走到相邻的数字不同的位置”,现在给定m次询问
(u,v),输出从(u,v)开始最多可以走多少个位置?思路:我们可以将此问题转化为一个求解连通块的问题。对于矩阵中的一个连通块,我们定义为:在其中任意一个位置开始行走,都可以走过整个连通块每一个位置。那么在询问时,只需要输出所在连通块元素的个数即可。现在将问题转化为了
如何遍历每一个连通块?按照标记数组的情况,如果一个位置没有被标记,就从这个位置出发开始打标记并统计
如何统计每一个连通块中元素的个数?按照题目中给定的迷宫行走规则,可以通过bfs或者dfs实现遍历
bfs代码
1 | |
dfs代码
1 | |
【dfs/二进制枚举】kkksc03考前临时抱佛脚
https://www.luogu.com.cn/problem/P2392
题意:给定四组数据,每组数据由 n 个数字组成,对于每一组数字需要分为两组使得两组之和相差尽可能小,问最终四组数据分组后,每一组之和的最大值之和是多少
思路一:二进制枚举
可以发现,我们可以只设计处理一组数据的算法,其余组数的数据调用该算法即可。对于一个序列,想要将其划分为 2 组使得 2 组之和的差值最小,我们可以发现,对于序列中的一个数而言,有两个状态,要么分到第一组,要么就分到第二组,因此我们可以采用二进制枚举的方式,将所有的分组情况全部枚举出来,每一个状态计算一下和的差值,最后取最小差值时,两组中和的最大值即可
时间复杂度:
O ( 4 × 2 n ) O(4 \times 2^n) 思路二:dfs
从上面的二进制枚举得到启发,一定可以进行二叉树搜索。很显然就直接左结点让当前数分到左组,右结点让当前数分到右组即可。本题无法剪枝,因为两组之和的差值没有规律
时间复杂度:
O ( 4 × 2 n ) O(4 \times 2^n)
二进制枚举代码
1 | |
dfs代码
1 | |
【dfs/二进制枚举】PERKET
https://www.luogu.com.cn/problem/P2036
题意:给定一个二元组序列,每一个二元组中,一个表示酸度,一个表示苦度,现在在至少需要选择一个二元组的情况下,希望酸度之积与苦度之和的差值最小
思路一:二进制枚举
很显然的一个二进制枚举。每一个二元组都只有两个状态,即被选择 or 不被选择,故可采用二进制枚举,对于每一个状态统计酸度之积与苦度之和即可
时间复杂度:
O ( 2 n ) O(2^n) 思路二:dfs
按照上述二进制枚举的思路进行模拟即可,本题无法剪枝,因为酸度与苦度之差没有规律
时间复杂度:
O ( 2 n ) O(2^n)
二进制枚举代码
1 | |
dfs代码
1 | |
【dfs】迷宫
https://www.luogu.com.cn/problem/P1605
题意:矩阵寻路,有障碍物,每一个点只能走一次,找到起点到终点可达路径数
思路:其实就是一个四叉树的题目,只需要进行四个方向的遍历搜索即可找到路径,由于会进行:越界、障碍物、以及不可重复遍历的剪枝,故遍历的数量会很少
时间复杂度:
< < O ( 4 n m ) << O(4^{nm})
1 | |
【dfs】单词方阵
https://www.luogu.com.cn/problem/P1101
- 题意:给定一个字符串方阵,问对于其中的 8 个方向,是否存在一个指定的字符串
- 思路:很显然的暴力枚举,只不过采用 dfs 进行优化,我们可以发现搜索的逻辑非常的简单,只需要在约束方向的情况下每次遍历八个方向即可。本题的关键在于如何快速正确的编码。对于八个角度判断是否与原始方向一致,我们采用增量的思路,只需要通过传递父结点的位置坐标即可唯一确定,因为两点确定一条了一条射线,方向也就确定了。其次就是如何构造答案矩阵,思路与两点确定射线的逻辑类似,我们在抵达搜索的终点时,只需要通过当前点的坐标与父结点的坐标唯一确定来的路径的方向,进行构造即可
- 时间复杂度:难以计算,但是 dfs 一定可行
1 | |
【dfs】自然数的拆分问题
https://www.luogu.com.cn/problem/P2404
- 题意:给定一个自然数 n,问有多少种拆分方法能将该数拆分为一定数量的升序自然数之和
- 思路:树形搜索的例题。我们采用递增凑数的思路,对于每一个结点值,我们从其父结点的值开始深度搜索,从而确保了和数递增。递归终点就是和值为自然数 n 的值。剪枝就是和值超过了自然数 n 的值
- 时间复杂度:
< < O ( n n ) <<O(n^n)
1 | |
【dfs】Lake Counting S
https://www.luogu.com.cn/problem/P1596
- 题意:给定一个矩阵,计算其中连通块的数量
- 思路:直接逐个元素遍历即可,对于每一个元素,我们采用 dfs 或者 bfs 的方式进行打标签从而将整个连通块都标记出来即可
- 时间复杂度:
O ( n m ) O(nm)
dfs 代码
1 | |
bfs 代码
1 | |
【dfs】填涂颜色
https://www.luogu.com.cn/problem/P1162
- 题意:给定一个方阵,其中只有 0 和 1,其中的 1 将部分的 0 围成了一个圈,现在需要将被围住的 0 转为 2 后,将转化后的方阵输出
- 思路:题意很简单,思路也很显然,我们要做的就是区分开圈内与圈外的 0,如何区分呢?我们采用搜索打标记的方式将外圈的 0 全部打标记之后,遇到的没有打标记的 0 显然就是圈内的了。为了满足所有情况下圈内的 0,我们从方阵的四条边进行探测式打标签即可
- 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【bfs】马的遍历
https://www.luogu.com.cn/problem/P1443
- 题意:给定一个矩阵棋盘范围与一个马的位置坐标,现在问棋盘中每一个点的最小到达距离是多少
- 思路:很显然的一个 bfs 宽搜模型,我们只需要从该颗马的起始位置开始宽搜,对于每一个第一个搜索到的此前没有到达的点,计算此时到起点的步长距离就是最小到达距离
- 时间复杂度:
O ( n × m ) O(n \times m)
1 | |
【bfs】奇怪的电梯
https://www.luogu.com.cn/problem/P1135
- 题意:给定一个电梯,第
i层只能上升或者下降a[i]层,问从起点开始到终点最少需要乘坐几次电梯- 思路:很显然的一个宽搜,关键在于需要对打标记避免重复访问结点造成死循环
- 时间复杂度:
O ( n ) O(n)
1 | |
【dfs/状压dp】吃奶酪 ⭐
题意:给定一个平面直角坐标系与 n 个点的坐标,起点在坐标原点。问如何选择行进路线使得到达每一个点且总路程最短
思路一:爆搜。题中的
直接无脑爆搜,但是 TLE。爆搜的思路为:每次选择其中的一个点,接下来选择剩余的没有被选择过的点继续搜索,知道所有的点全部都搜到为止 n ≤ 15 n \le 15 时间复杂度:
O ( n ! ) O(n!) 思路二:状态压缩 DP。
时间复杂度:
O ( ) O()
爆搜代码
1 | |
状压 dp 代码
1 | |
【dfs】递归实现指数型枚举
https://www.acwing.com/problem/content/94/
- 题意:给定 n 个数,从其中选择 0-n 个数,将所有的选择方案打印出来,每一个方案中数字按照升序排列
- 思路:很显然的一个二叉树问题。每一个数只有两种状态,选择 or 不选择,于是可以采用二进制枚举 or 二叉树 dfs 的方法进行。为了满足升序,二进制枚举时从低位到高位判断是否为 1 即可;搜索时从低位开始搜索,通过一个动态数组存储搜索路径上的数字即可
- 时间复杂度:
O ( 2 n ) O(2^n)
二进制枚举
1 | |
dfs
1 | |
【dfs】递归实现排列型枚举
https://www.acwing.com/problem/content/96/
- 题意:按照字典序升序,打印 n 个数的所有全排列情况
- 思路:从第一位开始枚举每一位可以选择的数,显然每一位可选择数的数量逐渐减少,直到只有一种选择结束搜索
- 时间复杂度:
O ( n ! ) O(n!)
1 | |
【dfs/树形dp】树的直径 ⭐
树的路径问题,考虑回溯。如何更新值?如何返回值?
参考:https://www.bilibili.com/video/BV17o4y187h1/
【dfs】在带权树网络中统计可连接服务器对数目
题意:给定一棵带权无根树,定义「中转结点」为以当前结点为根,能够寻找到两个不同分支下的结点,使得这两个结点到当前结点的简单路径长度可以被给定值 k 整除,问树中每一个结点的「中转结点」的有效对数是多少
思路:dfs+乘法原理。
- 由于数据量是
,可以直接枚举每一个顶点,并且每一个顶点的操作可以是 n = 1 0 3 n=10^3 的,我们考虑遍历。对于每一个结点,对应的有效对数取决于每一个子树中的简单路径长度合法的结点数,通过深搜统计即可 O ( n ) O(n) - 统计出每一个子树的合法结点后还需要进行答案的计算,也就是有效对数的统计。对于每一个合法结点,都可以和非当前子树上的所有结点结合形成一个合法有效对,直接这样统计会导致结果重复计算一次,因此需要答案除以二。当然也可以利用乘法原理,一边统计每一个子树中有效的结点数,一边和已统计过的有效结点数进行计算
时间复杂度:
O ( n 2 ) O(n^2) 注:总结本题根本原因是提升对建图的理解以及针对
vector用法的总结
- 关于建图
- 一开始编码时,我设置了结点访问状态数组
vector<bool> vis和每一个结点到当前根结点的距离数组vector<int> d,但其实都可以规避,因为本题是「树」形图,可以通过在深搜时同时传递父结点来规避掉vis数组的使用- 同时由于只需要在遍历时计算路径是否合法从而计数,因此不需要存储每一个结点到当前根结点的路径值,可以通过再增加一个搜索状态参数来规避掉
d数组的使用- 关于
vector
- 一开始使用了全局
vis数组,因此每次都需要进行清空操作。我使用了.clear()方法试图重新初始化数组,但这导致了状态的错误记录,可能是 LeetCode 平台 C++ 语言特有的坑,还是少用全局变量.clear()方法会导致.size()为 0,但是仍然可以通过[]方法获得合法范围内的元素值,这是vector内存分配优化的结果
1 | |
1 | |
【dfs】将石头分散到网格图的最少移动次数
https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/
标签:搜索、全排列、库函数
题意:给定一个
的矩阵 3 × 3 3\times 3 ,其中数字总和为 9 且 g g ,现在需要将其中 g [ i ] [ j ] ≥ 0 g[i][j] \ge 0 的数字逐个移动到值为 0 的位置上使得最终矩阵全为 1,问最少移动长度是多少。 > 1 >1 思路一:手写全排列
- 思路:可以将这道题抽象为求解「将 a 个大于 1 位置的数分配到 b 个 0 位置」的方案中的最小代价问题。容易联想到全排列选数的母问题:数字的位数对应这里的 b 个 0 位置,每个位置可以填的数对应这里的用哪个 a 来填。区别在于:0 的位置顺序不是固定的,用哪个 a 来填的顺序也不是固定的。这与全排列数中:被填的位置顺序是固定的,用哪个数来填不是固定的,有所区别。因此我们可以全排列枚举每一个位置,在此基础之上再全排列枚举每一个位置上可选的 a 进行填充。可以理解为全排列的嵌套。那么最终递归树的深度就是 0 的个数,递归时再用一个参数记录每一个选数分支对应的代价即可。
- 时间复杂度:
O ( 9 × 9 ! ) O(9\times 9!) 思路二:库函数全排列
- 思路:由于方阵的总和为 9,因此 >1 的位置上减去 1 剩下的数值之和一定等于方阵中 0 的个数。因此我们可以将前者展开为和 0 相同大小的向量,并全排列枚举任意一者进行两者的匹配计算,维护其中的最小代价即是答案。
- C++ 的全排列枚举库函数为
std::next_permutation(ItFirst, ItEnd)- Python 的全排列枚举库函数为
itertools.permutations(Iterable)- 时间复杂度:
O ( 9 × 9 ! ) O(9\times 9!)
1 | |
1 | |
1 | |
1 | |
动态规划分为被动转移和主动转移,而其根本在于状态表示和状态转移。如何完整表示所有状态?如何不重不漏划分子集从而进行状态转移?

【递推】反转字符串
https://www.acwing.com/problem/content/5574/
题意:给定 n 个字符串,每一个字符串对应一个代价
,现在需要对这 n 个字符串进行可能的翻转操作使得最终的 n 个字符串呈现字典序上升的状态,给出最小翻转代价。 w i w_i 思路:很显然每一个字符串都有两种状态,我们可以进行二叉搜索或者二进制枚举。那么我们可以进行 dp 吗?答案是可以的。我们可以发现,对于第 i 个字符串,是否需要翻转仅仅取决于第 i-1 个字符串的大小,无后效性,可以进行递推。我们定义状态数组
f[i][j]进行状态标识。其中
f[i][0]表示第 i 个字符串不需要翻转时的最小代价f[i][1]表示第 i 个字符串需要翻转时的最小代价状态转移就是当前一个字符串比当前字符串的字典序小时进行转移,即当前最小代价是前一个状态的最小代价加上当前翻转状态的代价。至于什么时候可以进行状态转移,一共有 4 种情况,即:
s[i-1]不翻转,s[i]不翻转。此时f[i][0] = min(f[i][0], f[i-1][0])s[i-1]翻转,s[i]不翻转。此时f[i][0] = min(f[i][0], f[i-1][1])s[i-1]不翻转,s[i]翻转。此时f[i][1] = min(f[i][1], f[i-1][0] + w[i])s[i-1]翻转,s[i]翻转。此时f[i][1] = min(f[i][1], f[i-1][1] + w[i])最终答案就在
f[n][0]和f[n][1]中取min即可时间复杂度:
O ( n ) O(n)
1 | |
【递推】最大化子数组的总成本
https://leetcode.cn/problems/maximize-total-cost-of-alternating-subarrays/
题意:给定长度为 n 的序列,现在需要将其分割为子数组,并定义每一个子数组的价值为「奇数位置为原数值,偶数位置为相反数」,返回最大分割价值
思路:~~一开始还在想着如何贪心,即仅考虑连续的负数区间,但是显然的贪不出全局最优解。~~于是转而考虑暴力 dp。思路和朴素 01 背包有相似之处。
状态定义。首先我们一定需要按照元素进行枚举,因此第一维度我们就定义为序列长度,但是仅仅这样定义就能表示全部的状态了吗?显然不行。根据题目的奇偶价值约束,我们在判定每一个负数是否可以「取相反数」价值时,是取决于上一个负数是否取了相反数价值。为了统一化,我们将正负数一起考虑前一个数是否取了相反价值的情况,因此我们需要再增加「前一个数是否取了相反价值」的状态表示,而这仅仅是一个二值逻辑,直接开两个空间即可。于是状态定义呼之欲出:
f[i][0]表示第i个数取原始价值的情况下,序列[0, i-1]的最大价值f[i][1]表示第i个数取相反价值的情况下,序列[0, i-1]的最大价值状态转移。显然对于上述状态定义,仅仅需要对「连续负数区间」进行考虑,因此对于
nums[i] >= 0的情况是没有选择约束的,原始价值和相反价值都是可行的方案那么为了最大化最终收益显然选择原始正价值,并且可以从上一个情况的任意状态转移过来那么同样为了最大化最终受益显然选择最大的基状态,于是可得:
f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]f[i][1] = max(f[i-1][0], f[i-1][1]) - nums[i]而对于
nunms[i] < 0的情况,能否选择相反数取决于前一个数的正负性。当前一个数nums[i-1] >= 0时,显然当前负数原始价值和相反价值都可以取到;当前一个数nums[i-1] < 0时,则当前负数仅有在前一个负数取原始价值的情况下才能取相反价值,于是可得:
if nums[i-1] >= 0
f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]f[i][1] = max(f[i-1][0], f[i-1][1] - nums[i])
if nums[i-1] < 0
f[i][0] = max(f[i-1][0], f[i-1][1] + nums[i])f[i][1] = f[i-1][0] - nums[i]答案表示。
max(f[n-1][0], f[n-1][1])时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【递推】费解的开关
https://www.acwing.com/problem/content/97/
题意:给定 n 个
5*5的矩阵,代表当前局面。矩阵中每一个元素要么是 0 要么是 1,现在需要计算从当前状态操作到全 1 状态最少需要几次操作?操作描述为改变当前状态为相反状态后,四周的四个元素也需要改变为相反的状态思路:我们采用递推的思路。为了尽可能少的进行按灯操作,我们从第二行开始考虑,若前一行的某一元素为 0,则下一行的同一列位置就需要按一下,以此类推将
行全部按完。现在考虑两点,当前按下状态是否合法?当前按下状态是是否最优? 2 → 5 2 \to 5
- 对于第一个问题:从上述思路可以看出,
行一定全部都是 1 的状态,但是第 1 → n − 1 1 \to n-1 行不一定全 1,因此不合法状态就是第 n − 1 n-1 行不全为 1 n − 1 n-1 - 对于第二个问题:可以发现,上述算法思路中,对于第一行是没有任何操作的(可以将第一行看做递推的初始化条件),第一行的状态影响全局的总操作数,我们不能确定不对第一行进行任何操作得到的总操作数就是最优的,故我们需要对第一行 5 个灯进行枚举按下。我们采用 5 位二进制的方法对第一行的 5 个灯进行枚举按下操作,然后对于当前第一行的按下局面(递推初始化状态)进行
行的按下递推操作。对于每一种合法状态更新最小的操作数即可 2 → n 2 \to n 时间复杂度:
O ( T × 2 5 × 25 × 5 ) O(T \times 2^5 \times 25 \times 5)
1 | |
【递推/线性dp/哈希】Decode
https://codeforces.com/contest/1996/problem/E
题意:给定一个01字符串,问所有区间中01数量相等的子串总共有多少个。
思路:
- 我们可以最直接的想到
的暴力做法,即 O ( n 5 ) O(n^5) 枚举区间的左右端点, O ( n 2 ) O(n^2) 枚举区间中子串的左右端点,最后 O ( n 2 ) O(n^2) 进行检查计数。当然可以用前缀和优化掉 O ( n ) O(n) 的检查计数。但这样做显然无法通过 O ( n ) O(n) 的数据量。考虑别的思路。 1 0 5 10^5 - 容易想到动态规划的思路。我们定义
dp[i]表示右端点是s[i]的所有区间中,合法01子串的数量,那么显然dp[0] = s[i] == '1'。现在考虑dp[i]如何转移。不难发现以s[i]为右端点的所有区间一定包含以s[i - 1]为右端点的所有区间,多出来的合法子串进存在于以s[i]结尾的子串中,我们假设以s[i]结尾的合法子串数量为t,则状态转移方程为:dp[i] = dp[i - 1] + t。显然我们可以用一个滚动变量来代替 dp 数组,记作now,每次维护完 now 以后,将其累加到答案即可。现在我们将枚举区间从通过递推的思路优化到了 O ( n 2 ) O(n^2) 。那么如何求解递推式中的 O ( n ) O(n) t呢?- 通过一个小 trick 求解「以
s[i]结尾的合法子串」的数量。显然可以通过前缀和枚举统计使得 j ∈ [ 1 , i ] j \in [1,i] i - j + 1 == 2 * (pre[i] - pre[j - 1])的数量。但是这样就是的了,仍然无法通过本题。引入 trick:我们稍微修改一下前缀和的维护逻辑,即当 O ( n 2 ) O(n^2) s[i] == '0'时,将其记作-1,当s[i] == '1'时,保持不变仍然记作1。这样我们在向前枚举j寻找合法区间时,本质上就是在寻找pre[i] - pre[j - 1] == 0,即pre[j - 1] == pre[i]的个数。假设下标从 0 开始,则每找到一个合法的j,都会对答案贡献j + 1。因此我们只需要哈希存储每一个前缀和对应的下标累计值即可。时间复杂度:
O ( n ) O(n)
1 | |
【递推/数学】Squaring
https://codeforces.com/contest/1995/problem/C
题意:给定一个序列,可以对其中任何一个数进行任意次平方操作,即
,问最少需要执行多少次操作可以使得序列不减。 a i → a i 2 a_i \to a_i^2 思路:
首先显然的我们不希望第一个数
变大,因此我们应该从第二个数开始和前一个数进行比较,从而进行可能的平方操作并计数。但是由于数字可能会很大,使用高精度显然会超时,而这些数字本身的意义是用来和前一个数进行大小比较的,并且变化的形式也仅仅是平方操作。我们不妨维护其指数,这样既可以进行大小比较,也不用存储数字本身而造成溢出。当然变为使用指数存储以后如何进行大小比较以及如何维护指数序列有所不同,我们先从一般的角度出发,进而从表达式本身的数学角度讨论特殊情况的处理。 a 0 a_0 对于当前数字
和前一个数字 a i a_i 及其指数 a i − 1 a_{i-1} ,如果想要当前数字经过可能的 k 次平方操作后不小于前一个数,即 z i − 1 z_{i-1} ,则易得下面的表达式: a i − 1 2 z i − 1 ≤ a i 2 k \displaystyle a_{i-1}^{2^{z_{i-1}}}\le a_i^{2^{k}}
k : = z i − 1 + ⌈ log 2 ( log 2 a i − 1 log 2 a i ) ⌉ k:= z_{i-1}+ \left\lceil \log_2(\frac{\log_2 {a_{i-1}}}{\log_2{a_i}}) \right \rceil 由于
,因此我们有必要: a j ∈ [ 1 , 1 0 6 ] , z j ≥ 0 , k ≥ 0 a_j \in [1, 10^6],z_j\ge 0,k \ge 0
- 讨论
和 a i a_i 和 a i − 1 a_{i-1} 的大小关系。因为它们的对数计算结果在真数部分。 1 1 - 讨论
和 k k 的大小关系。因为一旦 0 0 ,则有可能出现计算结果为负的情况,这种情况表明需要对当前数 a i − 1 < a i a_{i-1} < a_i 进行开根的操作。又由于 a i a_i ,因此开根操作就表明减小当前的数,也就表明当前数在不进行平方操作的情况下就已经满足不减的条件了,也就不需要操作了。此时对应的指数 a i ≥ 1 a_i\ge1 就是 z i z_i ,对于答案的贡献也是 0 0 。 0 0 时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【递推/dfs】牛的语言学
https://www.acwing.com/problem/content/description/5559/
题意:已知一个字符串由前段的一个词根和后段的多个词缀组成。词根的要求是长度至少为 5,词缀的要求是长度要么是 2, 要么是 3,以及不允许连续的相同词缀组成后段。现在给定最终的字符串,问一共有多少种词缀?按照字典序输出所有可能的词缀
思路一:搜索。很显然我们应该从字符串的最后开始枚举词缀进行搜索,因为词缀前面的所有字符全部都可以作为词根合法存在,我们只需要考虑当前划分出来的词缀是否合法即可。约束只有一个,不能与后面划分出来的词缀相同即可,由于我们是从后往前搜索,因此我们在搜索时保留后一个词缀即可。如果当前词缀和上一个词缀相同则返回,反之如果合法则加入 set 自动进行字典序排序。
时间复杂度:
O ( 2 n 2 ) O(2^{\frac{n}{2}}) 思路二:动态规划(递推)。动规其实就是 dfs 的逆过程,我们从已知结果判断当前局面是否合法。很显然词根是包罗万象的,只要长度合法,不管什么样的都是可行的,故我们在判断当前局面是否合法时,只需要判断当前词缀是否合法即可。于是便可知当前状态是从后面的字符串转移过来的。我们定义状态转移记忆数组
f[i]表示字符串s[1,i]是否可以组成词根。如果f[i]为真,则表示s[1,i]为一个合法的词根,s[i+1,n]为一个合法的词缀串,那么词根后面紧跟着的一定是一个长度为 2 或 3 的合法词缀。
我们以紧跟着长度为 2 的合法词缀为例。如果
s[i+1,i+2]为一个合法的词缀,则必须要满足以下两个条件之一
s[i+1,i+2]与s[i+3,i+4]不相等,即后面的后面是一个长度也为 2 且合法的词缀s[1,i+5]是一个合法的词根,即f[i+5]标记为真,即后面的后面是一个长度为 3 且合法的词缀以紧跟着长度为 3 的哈法词缀同理。如果
s[i+1,i+3]为一个合法的词缀,则必须要满足以下两个条件之一
s[i+1,i+3]与s[i+4,i+6]不相等,即后面的后面是一个长度也为 3 且合法的词缀s[1,i+5]是一个合法的词根,即f[i+5]标记为真,即后面的后面是一个长度为 2 且合法的词缀时间复杂度:
- O ( n log n ) O(n \log n) dp的过程是线性的,主要时间开销在set的自动排序上
dfs 代码
1 | |
dp 代码
1 | |
【线性dp】最小化网络并发线程分配
https://vijos.org/d/nnu_contest/p/1492
题意:现在有一个线性网络需要分配并发线程,每一个网络有一个权重,现在有一个线程分配规则。对于当前网络,如果权重比相邻的网络大,则线程就必须比相邻的网络大。
思路:我们从答案角度来看,对于一个网络,我们想知道它的相邻的左边线程数和右边线程数,如果当前网络比左边和右边的权重都大,则就是左右线程数的最大值+1,当然这些的前提是左右线程数已经是最优的状态,因此我们要先求“左右线程”。分析可知,左线程只取决于左边的权重与线程数,右线程同样只取决于右边的权重和线程数,因此我们可以双向扫描一遍即可求得“左右线程”。最后根据“左右线程”即可求得每一个点的最优状态。
1 | |
【线性dp】Block Sequence
https://codeforces.com/contest/1881/problem/E
题意:给定一个长为
的数组 a,问最少可以删除其中的几个元素,使得最终的数组可以被划分为连续的子数组且每一个子数组的元素个数均为「子数组首元素数值 n ≤ 2 × 1 0 5 n\le 2\times 10^5 」的形式。 − 1 -1 思路:
- 首先可以看出,序列的首元素一定是对应子数组剩余元素的个数。我们不妨倒序枚举每一个元素并定义
f[i]表示使数组a[i:]符合定义的最小删除次数,这样每次枚举到的元素都一定是所在子数组的首元素。- 接下来考虑状态转移。对于当前枚举到的元素
a[i],如果不删除,则f[i]将从f[i+a[i]+1]转移过来;如果删除,则f[i]将从f[i+1]转移过来。两者取最小值即可。时间复杂度
O ( n ) O(n)
1 | |
【线性dp】覆盖墙壁
https://www.luogu.com.cn/problem/P1990
题意:给定两种砖块,分别为日字型与L型,问铺满
的地板一共有多少种铺法 2 ∗ n 2*n 思路:
- 我们采用递推的思路
d e f i n e : define: f[i]表示铺满前个地板的方案数, 2 ∗ i 2*i g[i]表示铺满前块地板的方案数 2 ∗ i + 1 2*i+1 b a s e : base: f[0] = 1, f[1] = 1, g[0] = 0, g[1] = 1d p : dp: f[i] = f[i-1] + f[i-2] + g[i-1]∣ ∣ || g[i] = f[i-1] + g[i-1]r e s u l t : result: f[n]手绘:
1 | |
【线性dp】施咒的最大总伤害
https://leetcode.cn/problems/maximum-total-damage-with-spell-casting/
标签:线性 dp
题意:给定一个数组,选择一个子序列使得总和最大。约束为:如果选择了值为
的元素,则不允许选择值为 x x 的元素 x − 2 , x − 1 , x + 1 , x + 2 x-2,x-1,x+1,x+2 思路:
- 哈希计数。首先很显然的我们需要进行哈希计数,便于按数值升序枚举元素。我们定义哈希后的序列为
v,大小为m,存储每一种数的数值val: int和个数cnt: int- 状态定义。我们定义状态
f[i]表示哈希序列[1,i]中子序列总和的最大值,则最终答案就是f[m]- 状态转移。对于每一个哈希元素,都有选择和不选两种状态。假设当前枚举到的哈希元素为
i,
- 不选当前元素。就相当于没有当前元素,则
f[i] = f[i-1]- 选择当前元素。我们就需要从哈希序列
[1,i-1]中,比当前哈希元素v[i].val小 2 且对应子序列之和最大的那个状态f[j]转移过来。显然我们可以直接枚举哈希序列[1,i-1],但是这样就是必然超时,考虑优化。不难发现 O ( n 2 ) O(n^2) f[]数组是单调递增的并且哈希序列的元素数值v[].val也是单调递增的。也就是说对于当前状态f[i],在枚举哈希序列[1,i-1]时,其实并不需要从1开始枚举,可以从上一个状态枚举到的状态(记作j)开始枚举(因为上一个状态对应的f[j]是上一个状态可转移的方案中最大的并且v[j].val一定比当前方案的哈希数值v[i].val小 2)。于是状态转移的时间开销就从优化到 O ( n ) O(n) ,可以通过此题 O ( 1 ) O(1) 时间复杂度:
O ( n ) O(n) 空间复杂度:
O ( n ) O(n)
1 | |
1 | |
【线性dp】奇怪的汉诺塔
https://www.acwing.com/problem/content/98/
题意:四塔汉诺塔问题。求在给定
个圆盘的情况下的最少移动方案数。 n n 思路:
我们定义「最小完成单元」为:在满足游戏规则的情况下,将一座塔的所有圆盘移动到另一座塔所需的最少塔数。那么显然的最小完成单元为 3 座塔。定义
d[i]表示三塔模式下个盘的最少移动次数, i i f[i]表示四塔模式下个盘的最少移动次数。 i i 对于 4 座塔的情况,相当于最小完成单元又多了 1 座塔。那么显然多出来的这座塔有两个处置方案:
如果我们不利用这座塔。那么还剩 3 座塔,也就是最小完成单元,此时的最少移动次数是唯一的,也就是
f[i] = d[i]如果我们要利用这座塔。那么我们只能在这一座塔上按规则放圆盘。因为要确保最小完成单元来让剩余的圆盘移动到另一座塔。如果还在别的塔上放置了圆盘,那么将不符合最小完成单元的定义,游戏无法结束。当然我们不能将所有的圆盘都先放到这座塔上,因为这种情况下是不可能成立的,我们不可能让一个「我们正在求解的问题」作为我们的答案。也就是说
j < i j<i 至此四塔模式下
个圆盘游戏方案的组成集合已全部确定,如下图所示,即:在四塔模式下移动 i i 个圆盘到其中一座空塔上,方案数为 j ∈ [ 0 , i − 1 ] j \in [0,i-1] ;剩余的 f [ j ] f[j] 个圆盘处于最小完成单元的局面,方案数是唯一的 i − j i-j ;最后再将一开始移动的 d [ i − j ] d[i-j] 个圆盘在四塔模式下移动到刚才剩余圆盘移动到的塔上,方案数为 j j 。 f [ j ] f[j]
于是最终的状态转移方程为:
f i = min { f j + d i − j + f j } , i ∈ [ 1 , n ] , j ∈ [ 0 , i − 1 ] f_i = \min{ \{ f_j+d_{i-j}+f_j \} },\quad i \in [1,n],\quad j \in [0,i-1] 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【线性dp/dfs】数的计算
https://www.luogu.com.cn/problem/P1028
题意:给定一个数和一种构造方法,即对于当前的数,可以在其后面添加一个最大为当前一半大的数,以此类推构造成一个数列。问一共可以构造出多少个这种数列
思路一:dfs
- 非常显然的一个搜索树,答案就是结点数
- 时间复杂度:
O ( 方案数 ) O(\text{方案数}) 思路二:dp
非常显然的一个dp,我们定义一个dp记忆数组。其中
dp[i]表示数字i的构造方案总数,那么状态转移方程就是
d p [ i ] = ∑ j = 1 ⌊ i / 2 ⌋ d p [ j ] + 1 dp[i]=\sum_{j=1}^{\left\lfloor i/2 \right\rfloor}dp[j]+1 时间复杂度:
O ( n 2 ) O(n^2)
dfs代码
1 | |
dp代码
1 | |
【线性dp/二分答案】规划兼职工作
https://leetcode.cn/problems/maximum-profit-in-job-scheduling/description/
题意:给定 n 份工作的起始时间、终止时间、收益值,现在需要不重叠时间的选择工作使得收益最大
思路:动态规划、二分答案。为了不重不漏的枚举每一份工作,我们将工作按照结束时间进行排序,然后就可以枚举每一份工作了。接下来要解决的问题是,如何根据起始时间和终止时间进行工作的选择。显然的,每一份工作有选与不选两种状态,是否选择取决于收益是否更优,我们考虑动态规划。我们定义状态表
f[i]表示在前 i 个工作中选择的最大工作收益,返回值就是f[n],先看图
- 选择第 i 个工作:
f[i] = f[r] + profit[i](其中 r 表示[1,i-1]份工作中,结束时间早于当前工作起始时间的最右边的工作,在[1,i-1]中二分查找即可)- 不选第 i 个工作:
f[i] = f[i - 1]选择最大属性进行状态转移即可:
f[i] = max(f[i - 1], f[r] + profit[i])时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【线性dp/二分查找】最长上升子序列
https://www.luogu.com.cn/problem/B3637
题意:给定序列,求解其中最长上升子序列 (Longest Increasing Subsequence, 简称 LIS) 的长度。
思路:我们采用动态规划。
状态定义:定义状态数组
f[i]表示以元素a[i]结尾的最长上升子序列的长度,显然的初始状态全都是1状态转移:
暴力枚举。首先很显然的
f[i]一定是从[0,i-1]中比当前元素值小的状态转移过来,于是可以很轻松的写出双重循环的代码,时间复杂度。 O ( n 2 ) O(n^2) 贪心+二分优化。
回顾朴素。优化需要在理解转移本质的基础上展开,因此我们先来回顾一下朴素版的转移方案:从
[0,i-1]中比当前元素小的元素a[j]对应的最长上升子序列长度f[j]转移过来。我们枚举了[0,i-1]所有的状态确保了不重不漏。对于i = 6来说,如下图所示。其中✔表示进入了if的判断逻辑。最终我们选择从j = 5对应的f[j] = 3转移而来。这里的判断准则为:对于每一个元素,需要找前面的元素中比当前元素小的元素。
转换视角。同样对于每一个元素
a[i],我们不再按顺序枚举前面已经计算出来的f[1:i-1],而是预先按照长度存储所有的f[1:i-1]从而枚举长度j,显然可以贪心的从最大长度mxa_len开始枚举。一旦遇到比a[i]小的元素,那么f[i]就等于当前枚举的长度+1,即f[i] = j + 1。对于i = 6来说,如下图所示。这样也可以做到不重不漏的枚举所有状态。但是显然的,这种方法只是变相地枚举了所有的元素,仍然是,并且和枚举元素相比还多了一点思维量和代码量。 O ( n 2 ) O(n^2)
优化诞生。在枚举元素时,并没有额外有价值的信息,比如元素并非单调排列,
f[]数组也并非单调。但转换到枚举长度,让我们有机会进行优化!不难发现,对于每一个元素a[i],我们在按长度[1,max_len]枚举可能的尾元素f[1:i-1]时,由于max_len每一次更新时的增量都是 1,因此[1,max_len]的每一个取值都一定会有对应的元素存在!贪心的,对于同一个长度下所有子序列的尾元素,我们只关心其中值最小的那一个尾元素,因此我们定义一个mi[]数组来存储每一个长度下子序列尾元素的最小值,其中mi[i]表示长度为i的最长上升子序列中,最小的尾元素值。这样在枚举长度[1,max_len]时,就不再需要枚举每一个长度下所有的尾元素,仅需枚举每一个长度下唯一的那个最小尾元素。但如果每一个长度都刚好只有一个元素,那岂不是还是需要线性枚举?更进一步的,我们可以发现,此时每一个长度对应的唯一元素组成的序列是严格单调递增的(反证法易证)!有了这样单调的性质我们就可以利用二分加速枚举,这样可以将枚举的时间复杂度严格控制在。显然的,我们希望当前的元素可以拼接在尽可能长的子序列后面,因此此处的二分使用的是寻找右边界的板子。 O ( log n ) O(\log n)
代码实现。枚举每一个元素肯定是少不了的,我们使用
mi[j]表示最长上升子序列长度为j的序列尾元素的最小值。初始状态显然就是mi[1] = a[0]。在每一个元素二分查询「最大的比当前元素小的元素」时,如果查出来的元素mi[r]确实比当前元素小,则需要更新mi[r+1]的值;反之如果查出来的元素mi[r]比当前元素还小,则表明二分到了左边界,此时r一定是 1,直接用当前元素覆盖mi[1]即可。答案表示。最终答案就是
max_len时间复杂度:
O ( n log n ) O(n \log n)
暴力枚举元素
1 | |
暴力枚举长度
1 | |
贪心二分优化
1 | |
【网格图dp/dfs】过河卒
https://www.luogu.com.cn/problem/P1002
题意:给定一个矩阵,现在需要从左上角走到右下角,问一共有多少种走法?有一个特殊限制是,对于图中的9个点是无法通过的。
思路一:dfs
我们可以采用深搜的方法。但是会超时,我们可以这样估算时间复杂度:对于每一个点,我们都需要计算当前点的右下角的矩阵中的每一个点,那么总运算次数就近似为阶乘级别。当然实际的时间复杂度不会这么大,但是这种做法
一旦超过100就很容易tle n ∗ m n*m 时间复杂度:
O ( n m ! ) O(nm!) 思路二:dp
我们可以考虑,对于当前的点,可以从哪些点走过来,很显然就是上面一个点和左边一个点,而对于走到当前这个点的路线就是走到上面的点和左边的点的路线之和,base状态就是
dp[1][1] = 1,即起点的路线数为1时间复杂度:
O ( n m ) O(nm)
dfs代码
1 | |
dp代码
1 | |
【网格图dp】摘樱桃 II
https://leetcode.cn/problems/cherry-pickup-ii/
题意:给定一个
行 n n 列的网格图,每个格子拥有一个价值。现在有两个人分别从左上角和右上角开始移动,移动方式为「左下、下、右下」三个方向,问两人最终最多一共可以获得多少价值?如果两人同时经过一个位置,则只能算一次价值。 m m 思路:
状态定义。最终状态一定是两人都在最后一行的任意两列,我们如何定义状态可以不重不漏的表示两人的运动状态呢?可以发现两人始终在同一行,但是列数不一定相同,我们定义状态
表示两人走到第 f [ i ] [ j ] [ k ] f[i][j][k] 行时,一人在第 i i 列,另一人在第 j j 列时的总价值。则答案就是: k k
max ( f [ n − 1 ] [ j ] [ k ] ) , j , k ∈ [ 0 , m ] \max{(f[n-1][j][k])},j,k\in[0,m] 状态转移。本题难点在于状态定义,一旦定义好了以后状态转移就不困难了。对于当前状态
,根据乘法原理,两人均有 3 种走法,因此当前状态可以从 f [ i ] [ j ] [ k ] f[i][j][k] 种合法状态转移过来。取最大值即可。 3 × 3 = 9 3\times 3=9 时间复杂度:
O ( n m 2 ) O(nm^2)
1 | |
【网格图dp】摘樱桃
弱化版
强化版
题意:给定一个 n 行 n 列的网格图,问从左上走到右下,再从右下走到左上最多可以获得多少价值?一个单元格只能被计算一次价值。
注:弱化版中 -1 表示不可达,强化版没有不可达的约束。强化版 AC 代码
思路一:暴力dp
- 首先对于来回问题可以转化为两次去的问题,即问题等价于求解「两个人从左上角走到右下角」的最大收益。
- 显然我们可以定义四维的状态,其中
表示第一个人走到 f [ i ] [ j ] [ p ] [ q ] f[i][j][p][q] 且第二个人走到 ( i , j ) (i,j) 时的最大收益。直接枚举这四个维度,然后从 4 个合法的子问题转移过来即可。 ( p , q ) (p,q) - 时间复杂度:
O ( n 4 ) O(n^4) 思路二:优化dp
- 注意到问题可以进一步等价于「两个人同时从左上角走到右下角」的最大收益。也就是两个人到起点
的曼哈顿距离应该是一样的,即 ( 0 , 0 ) (0,0) ,也就是说如果其中一个人 i + j = p + q i+j=p+q 的位置确定了,则另一个人只需要枚举一个下标,另一个下标就可以 ( i , j ) (i,j) 的确定了。可以将时间复杂度降低一个维度。 O ( 1 ) O(1) - 状态定义。我们定义
表示第一个人走到 f [ k ] [ i 1 ] [ i 2 ] f[k][i_1][i_2] 且第二个人走到 ( i 1 , k − i 1 ) (i_1,k-i_1) 时的最大收益。则最终答案就是 ( i 2 , k − i 2 ) (i_2,k-i_2) 。状态转移同理,从 4 个合法子问题转移过来即可。 f [ 2 n − 2 ] [ n − 1 ] [ n − 1 ] f[2n-2][n-1][n-1] - 时间复杂度:
O ( n 3 ) O(n^3)
暴力dp:
1 | |
优化dp:
1 | |
【树形dp】最大社交深度和
https://vijos.org/d/nnu_contest/p/1534
算法:树形dp、BFS
题意:给定一棵树,现在需要选择其中的一个结点为根节点,使得深度和最大。深度的定义是以每个结点到树根所经历的结点数
思路一:暴力
显然可以直接遍历每一个结点,计算每个结点的深度和,然后取最大值即可
时间复杂度:
O ( n 2 ) O(n^2) 思路二:树形dp
我们可以发现,对于当前的根结点
fa,我们选择其中的一个子结点ch,将ch作为新的根结点(如右图)。那么对于当前的ch的深度和,我们可以借助fa的深度和进行求解。我们假设以ch为子树的结点总数为x,那么这x个结点在换根之后,相对于ch的深度和,贡献了-x的深度;而对于fa的剩下来的n-x个结点,相对于ch的深度和,贡献了n-x的深度。于是ch的深度和就是fa的深度和-x+n-x,即:
d e p [ c h ] = d e p [ f a ] − x + n − x = d e p [ f a ] + n − 2 × x dep[ch] = dep[fa]-x+n-x = dep[fa]+n-2\times x 于是我们很快就能想到利用前后层的递推关系,
的计算出所有子结点的深度和。 O ( 1 ) O(1) 代码实现:我们可以先计算出
base的情况,即任选一个结点作为根结点,然后基于此进行迭代计算。在迭代计算的时候需要注意的点就是在一遍dfs计算某个结点的深度和dep[root]时,如果希望同时计算出每一个结点作为子树时,子树的结点数,显然需要分治计算一波。关于分治的计算我熟练度不够高,特此标注一下debug了3h的点:即在递归到最底层,进行回溯计算的时候,需要注意不能统计父结点的结点值(因为建的是双向图,所以一定会有从父结点回溯的情况),那么为了避开这个点,就需要在的时间复杂度内获得当前结点的父结点的编号,从而进行特判,采用的方式就是增加递归参数 O ( 1 ) O(1) fa。没有考虑从父结点回溯的情况的dfs代码
2
3
4
5
6
7
8
9
10void dfs(int now, int depth) {
if (!st[now]) {
st[now] = true;
dep[root] += depth;
for (auto& ch: G[now]) {
dfs(ch, depth + 1);
cnt[now] += cnt[ch];
}
}
}考虑了从父结点回溯的情况的dfs代码
2
3
4
5
6
7
8
9
10
11
12void dfs(int now, int fa, int depth) {
if (!st[now]) {
st[now] = true;
dep[root] += depth;
for (auto& ch: G[now]) {
dfs(ch, now, depth + 1);
if (ch != fa) {
cnt[now] += cnt[ch];
}
}
}
}时间复杂度:
Θ ( 2 n ) \Theta(2n)
暴力代码:
1 | |
优化代码:
1 | |
【高维dp/dfs】栈
https://www.luogu.com.cn/problem/P1044
题意:n个数依次进栈,随机出栈,问一共有多少种出栈序列?
思路一:dfs
- 我们可以这么构造搜索树:已知对于当前的栈,一共有两种状态
- 入栈 - 如果当前还有数没有入栈
- 出栈 - 如果当前栈内还有元素
- 搜索参数:
i,j表示入栈数为i出栈数为j的状态- 搜索终止条件
- 入栈数 < 出栈数 -
i < j i<j - 入栈数 > 总数
- n n i = n i = n - 答案状态:入栈数为n,出栈数也为n
- 时间复杂度:
O ( 方案数 ) O(\text{方案数}) 思路二:dp
采用上述dfs时的状态表示方法,
i,j表示入栈数为i出栈数为j的状态。我们在搜索的时候,考虑的是接下来可以搜索的状态
即出栈一个数的状态 -
i+1,j和入栈一个数的状态 -
i,j+1如图:
而我们在dp的时候,需要考虑的是子结构的解来得出当前状态的答案,就需要考虑之前的状态。即当前状态是从之前的哪些状态转移过来的。和上述dfs思路是相反的。我们需要考虑的是
- 上一个状态入栈一个数到当前状态 -
i-1,j→ \to i,j- 上一个状态出栈一个数到当前状态 -
i,j-1→ \to i,j
- 特例:
时,只能是上述第二种状态转移而来,因为要始终保证入栈数大于等于出栈数,即 i = j i=j i ≥ j i \ge j 如图:
我们知道,入栈数一定是大于等于出栈数的,即
。于是我们在枚举 i ≥ j i\ge j 的时候,枚举的范围是 j j [ 1 , i ] [1,i]
状态的构建取决于 b a s e base 时的所有状态,我们知道没有任何数出栈也是一种状态,于是 j = 0 j=0
d p [ i ] [ 0 ] = 0 , ( i = 1 , 2 , 3 , . . . , n ) dp[i][0]=0,(i=1,2,3,...,n) 时间复杂度:
O ( n 2 ) O(n^2)
dfs代码
1 | |
dp代码
1 | |
【高维dp】找出所有稳定的二进制数组 II
https://leetcode.cn/problems/find-all-possible-stable-binary-arrays-ii/
题意:构造一个仅含有
个 n n , 0 0 个 m m 的数组,且长度超过 1 1 的子数组必须同时含有 k k 和 0 0 。给出构造的总方案数对 1 1 取余后的结果。 1 0 9 + 7 10^9+7 思路:
定义状态表。我们从左到右确定每一位的数字时,需要确定这么三个信息:当前是哪一位?还剩几个
和 0 0 ?这一位填 1 1 还是 0 0 ?对于这三个信息,我们可以定义状态数组 1 1 表示当前已经选了 f [ i ] [ j ] [ k ] f[i][j][k] 个 i i , 0 0 个 j j ,且第 1 1 位填 i + j i+j 时的方案数。这样最终答案就是 k k 。 f [ n ] [ m ] [ 0 ] + f [ n ] [ m ] [ 1 ] f[n][m][0]+f[n][m][1] 定义子问题。以当前第
位填 i + j i+j 为例,填 0 0 同理,即当前需要维护的是 1 1 。显然的如果前一位是和当前位不同,即 f [ i ] [ j ] [ 0 ] f[i][j][0] 时,可以直接转移过来;如果前一位和当前位相同,即 1 1 时,有可能会出现长度超过 0 0 的连续 k k 子数组,即前段数组刚好是以「一个 0 0 和 1 1 个 k k 结尾的」合法数组,此时再拼接一个 0 0 就不合法了。 0 0 状态转移方程。综上所述,可以得到以下两个状态转移方程:
f [ i ] [ j ] [ 0 ] = f [ i − 1 ] [ j ] [ 1 ] + f [ i − 1 ] [ j ] [ 0 ] − f [ i − k − 1 ] [ j ] [ 1 ] f [ i ] [ j ] [ 1 ] = f [ i ] [ j − 1 ] [ 0 ] + f [ i ] [ j − 1 ] [ 1 ] − f [ i ] [ j − k − 1 ] [ 0 ] \begin{aligned}f[i][j][0] = f[i - 1][j][1] + f[i - 1][j][0] - f[i - k - 1][j][1] \\f[i][j][1] = f[i][j - 1][0] + f[i][j - 1][1] - f[i][j - k - 1][0]\end{aligned} 时间复杂度:
O ( n m ) O(nm)
1 | |
【高维dp】学生出勤记录 II
https://leetcode.cn/problems/student-attendance-record-ii/description/
题意:构造一个仅含有
三种字符的字符串,使得 P , A , L P,A,L 最多出现 A A 次,同时 1 1 最多连续出现 L L 次。问一共有多少种构造方案?对 2 2 取模。 1 0 9 + 7 10^9+7 思路:
- 模拟分析问题。我们从前往后构造。对于当前第
个字符 i i ,有 s [ i ] s[i] 种可能的选项,其中 3 3 是一定合法的选项, P P 是否合法取决于 A A 中的 s [ 0 : i − 1 ] s[0:i-1] 的数量, A A 是否合法取决于 L L 的末尾连续 s [ 0 : i − 1 ] s[0:i-1] 的数量。因此我们可以通过被动转移的动态规划求解。 L L - 状态定义。从上述分析不难发现需要
种状态来表示所有情况,因此我们定义 3 3 表示构造第 f [ i ] [ j ] [ k ] f[i][j][k] 位时, i i 中含有 s [ 0 : i ] s[0:i] 个 j j 且末尾含有连续 A A 个 k k 时的方案数。 L L - 初始化。每一位填什么取决于前缀
的情况,因此我们需要初始化 s [ 0 : i − 1 ] s[0:i-1] 即第 f [ 0 ] [ ] [ ] f[0][][] 位的情况。显然的第 0 0 位 0 0 三种都可以填,对应的就是 P , A , L P,A,L ,其余初始化为 f [ 0 ] [ 0 ] [ 0 ] = f [ 0 ] [ 1 ] [ 0 ] = f [ 0 ] [ 0 ] [ 1 ] = 1 f[0][0][0] = f[0][1][0] = f[0][0][1] = 1 即可。 0 0 - 状态转移。考虑第
位的三种情况: i i
- 填
:可以用前缀的所有状态来更新 P P f [ i ] [ j ] [ 0 ] f[i][j][0] - 填
:可以用前缀中不含 A A 的所有状态来更新 A A f [ i ] [ 1 ] [ 0 ] f[i][1][0] - 填
:可以用前缀中末尾不超过 L L 位 1 1 的所有状态来更新 L L f [ i ] [ j ] [ k ] f[i][j][k] - 最终答案。为
。 ∑ j = 0 1 ∑ k = 0 2 f [ n − 1 ] [ j ] [ k ] \displaystyle \sum_{j=0}^{1}\sum_{k=0}^{2}f[n-1][j][k] 时间复杂度:
Θ ( 6 n ) \Theta (6n)
1 | |
1 | |
【区间dp】对称山脉
https://www.acwing.com/problem/content/5169/
模拟,时间复杂度
1 | |
dp优化,时间复杂度
1 | |
【状压dp】Avoid K Palindrome 🔥
https://atcoder.jp/contests/abc359/tasks/abc359_d
题意:给定一个长度为
的字符串 n ≤ 1000 n\le 1000 和一个整数 s s ,其中含有若干个 k ≤ 10 k\le10 'A','B'和'?'。其中'?'可以转化为'A'或'B',假设有和 q q '?',则一共可以转化出个不同的 2 q 2^q 。问所有转化出的 s s 中,有多少是不含有长度为 s s 的回文子串的。 k k 思路:最暴力的做法就是 2^q 枚举所有可能的字符串,然后再 O(n) 的检查,这样时间复杂度为
,只能通过 20 以内的数据。一般字符串回文问题可以考虑 dp。 O ( n 2 n ) O(n2^n) 时间复杂度:
1 | |
动态规划分为被动转移和主动转移,而其根本在于状态表示和状态转移。如何完整表示所有状态?如何不重不漏划分子集从而进行状态转移?

【递推】反转字符串
https://www.acwing.com/problem/content/5574/
题意:给定 n 个字符串,每一个字符串对应一个代价
,现在需要对这 n 个字符串进行可能的翻转操作使得最终的 n 个字符串呈现字典序上升的状态,给出最小翻转代价。 w i w_i 思路:很显然每一个字符串都有两种状态,我们可以进行二叉搜索或者二进制枚举。那么我们可以进行 dp 吗?答案是可以的。我们可以发现,对于第 i 个字符串,是否需要翻转仅仅取决于第 i-1 个字符串的大小,无后效性,可以进行递推。我们定义状态数组
f[i][j]进行状态标识。其中
f[i][0]表示第 i 个字符串不需要翻转时的最小代价f[i][1]表示第 i 个字符串需要翻转时的最小代价状态转移就是当前一个字符串比当前字符串的字典序小时进行转移,即当前最小代价是前一个状态的最小代价加上当前翻转状态的代价。至于什么时候可以进行状态转移,一共有 4 种情况,即:
s[i-1]不翻转,s[i]不翻转。此时f[i][0] = min(f[i][0], f[i-1][0])s[i-1]翻转,s[i]不翻转。此时f[i][0] = min(f[i][0], f[i-1][1])s[i-1]不翻转,s[i]翻转。此时f[i][1] = min(f[i][1], f[i-1][0] + w[i])s[i-1]翻转,s[i]翻转。此时f[i][1] = min(f[i][1], f[i-1][1] + w[i])最终答案就在
f[n][0]和f[n][1]中取min即可时间复杂度:
O ( n ) O(n)
1 | |
【递推】最大化子数组的总成本
https://leetcode.cn/problems/maximize-total-cost-of-alternating-subarrays/
题意:给定长度为 n 的序列,现在需要将其分割为子数组,并定义每一个子数组的价值为「奇数位置为原数值,偶数位置为相反数」,返回最大分割价值
思路:~~一开始还在想着如何贪心,即仅考虑连续的负数区间,但是显然的贪不出全局最优解。~~于是转而考虑暴力 dp。思路和朴素 01 背包有相似之处。
状态定义。首先我们一定需要按照元素进行枚举,因此第一维度我们就定义为序列长度,但是仅仅这样定义就能表示全部的状态了吗?显然不行。根据题目的奇偶价值约束,我们在判定每一个负数是否可以「取相反数」价值时,是取决于上一个负数是否取了相反数价值。为了统一化,我们将正负数一起考虑前一个数是否取了相反价值的情况,因此我们需要再增加「前一个数是否取了相反价值」的状态表示,而这仅仅是一个二值逻辑,直接开两个空间即可。于是状态定义呼之欲出:
f[i][0]表示第i个数取原始价值的情况下,序列[0, i-1]的最大价值f[i][1]表示第i个数取相反价值的情况下,序列[0, i-1]的最大价值状态转移。显然对于上述状态定义,仅仅需要对「连续负数区间」进行考虑,因此对于
nums[i] >= 0的情况是没有选择约束的,原始价值和相反价值都是可行的方案那么为了最大化最终收益显然选择原始正价值,并且可以从上一个情况的任意状态转移过来那么同样为了最大化最终受益显然选择最大的基状态,于是可得:
f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]f[i][1] = max(f[i-1][0], f[i-1][1]) - nums[i]而对于
nunms[i] < 0的情况,能否选择相反数取决于前一个数的正负性。当前一个数nums[i-1] >= 0时,显然当前负数原始价值和相反价值都可以取到;当前一个数nums[i-1] < 0时,则当前负数仅有在前一个负数取原始价值的情况下才能取相反价值,于是可得:
if nums[i-1] >= 0
f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]f[i][1] = max(f[i-1][0], f[i-1][1] - nums[i])
if nums[i-1] < 0
f[i][0] = max(f[i-1][0], f[i-1][1] + nums[i])f[i][1] = f[i-1][0] - nums[i]答案表示。
max(f[n-1][0], f[n-1][1])时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【递推】费解的开关
https://www.acwing.com/problem/content/97/
题意:给定 n 个
5*5的矩阵,代表当前局面。矩阵中每一个元素要么是 0 要么是 1,现在需要计算从当前状态操作到全 1 状态最少需要几次操作?操作描述为改变当前状态为相反状态后,四周的四个元素也需要改变为相反的状态思路:我们采用递推的思路。为了尽可能少的进行按灯操作,我们从第二行开始考虑,若前一行的某一元素为 0,则下一行的同一列位置就需要按一下,以此类推将
行全部按完。现在考虑两点,当前按下状态是否合法?当前按下状态是是否最优? 2 → 5 2 \to 5
- 对于第一个问题:从上述思路可以看出,
行一定全部都是 1 的状态,但是第 1 → n − 1 1 \to n-1 行不一定全 1,因此不合法状态就是第 n − 1 n-1 行不全为 1 n − 1 n-1 - 对于第二个问题:可以发现,上述算法思路中,对于第一行是没有任何操作的(可以将第一行看做递推的初始化条件),第一行的状态影响全局的总操作数,我们不能确定不对第一行进行任何操作得到的总操作数就是最优的,故我们需要对第一行 5 个灯进行枚举按下。我们采用 5 位二进制的方法对第一行的 5 个灯进行枚举按下操作,然后对于当前第一行的按下局面(递推初始化状态)进行
行的按下递推操作。对于每一种合法状态更新最小的操作数即可 2 → n 2 \to n 时间复杂度:
O ( T × 2 5 × 25 × 5 ) O(T \times 2^5 \times 25 \times 5)
1 | |
【递推/线性dp/哈希】Decode
https://codeforces.com/contest/1996/problem/E
题意:给定一个01字符串,问所有区间中01数量相等的子串总共有多少个。
思路:
- 我们可以最直接的想到
的暴力做法,即 O ( n 5 ) O(n^5) 枚举区间的左右端点, O ( n 2 ) O(n^2) 枚举区间中子串的左右端点,最后 O ( n 2 ) O(n^2) 进行检查计数。当然可以用前缀和优化掉 O ( n ) O(n) 的检查计数。但这样做显然无法通过 O ( n ) O(n) 的数据量。考虑别的思路。 1 0 5 10^5 - 容易想到动态规划的思路。我们定义
dp[i]表示右端点是s[i]的所有区间中,合法01子串的数量,那么显然dp[0] = s[i] == '1'。现在考虑dp[i]如何转移。不难发现以s[i]为右端点的所有区间一定包含以s[i - 1]为右端点的所有区间,多出来的合法子串进存在于以s[i]结尾的子串中,我们假设以s[i]结尾的合法子串数量为t,则状态转移方程为:dp[i] = dp[i - 1] + t。显然我们可以用一个滚动变量来代替 dp 数组,记作now,每次维护完 now 以后,将其累加到答案即可。现在我们将枚举区间从通过递推的思路优化到了 O ( n 2 ) O(n^2) 。那么如何求解递推式中的 O ( n ) O(n) t呢?- 通过一个小 trick 求解「以
s[i]结尾的合法子串」的数量。显然可以通过前缀和枚举统计使得 j ∈ [ 1 , i ] j \in [1,i] i - j + 1 == 2 * (pre[i] - pre[j - 1])的数量。但是这样就是的了,仍然无法通过本题。引入 trick:我们稍微修改一下前缀和的维护逻辑,即当 O ( n 2 ) O(n^2) s[i] == '0'时,将其记作-1,当s[i] == '1'时,保持不变仍然记作1。这样我们在向前枚举j寻找合法区间时,本质上就是在寻找pre[i] - pre[j - 1] == 0,即pre[j - 1] == pre[i]的个数。假设下标从 0 开始,则每找到一个合法的j,都会对答案贡献j + 1。因此我们只需要哈希存储每一个前缀和对应的下标累计值即可。时间复杂度:
O ( n ) O(n)
1 | |
【递推/数学】Squaring
https://codeforces.com/contest/1995/problem/C
题意:给定一个序列,可以对其中任何一个数进行任意次平方操作,即
,问最少需要执行多少次操作可以使得序列不减。 a i → a i 2 a_i \to a_i^2 思路:
首先显然的我们不希望第一个数
变大,因此我们应该从第二个数开始和前一个数进行比较,从而进行可能的平方操作并计数。但是由于数字可能会很大,使用高精度显然会超时,而这些数字本身的意义是用来和前一个数进行大小比较的,并且变化的形式也仅仅是平方操作。我们不妨维护其指数,这样既可以进行大小比较,也不用存储数字本身而造成溢出。当然变为使用指数存储以后如何进行大小比较以及如何维护指数序列有所不同,我们先从一般的角度出发,进而从表达式本身的数学角度讨论特殊情况的处理。 a 0 a_0 对于当前数字
和前一个数字 a i a_i 及其指数 a i − 1 a_{i-1} ,如果想要当前数字经过可能的 k 次平方操作后不小于前一个数,即 z i − 1 z_{i-1} ,则易得下面的表达式: a i − 1 2 z i − 1 ≤ a i 2 k \displaystyle a_{i-1}^{2^{z_{i-1}}}\le a_i^{2^{k}}
k : = z i − 1 + ⌈ log 2 ( log 2 a i − 1 log 2 a i ) ⌉ k:= z_{i-1}+ \left\lceil \log_2(\frac{\log_2 {a_{i-1}}}{\log_2{a_i}}) \right \rceil 由于
,因此我们有必要: a j ∈ [ 1 , 1 0 6 ] , z j ≥ 0 , k ≥ 0 a_j \in [1, 10^6],z_j\ge 0,k \ge 0
- 讨论
和 a i a_i 和 a i − 1 a_{i-1} 的大小关系。因为它们的对数计算结果在真数部分。 1 1 - 讨论
和 k k 的大小关系。因为一旦 0 0 ,则有可能出现计算结果为负的情况,这种情况表明需要对当前数 a i − 1 < a i a_{i-1} < a_i 进行开根的操作。又由于 a i a_i ,因此开根操作就表明减小当前的数,也就表明当前数在不进行平方操作的情况下就已经满足不减的条件了,也就不需要操作了。此时对应的指数 a i ≥ 1 a_i\ge1 就是 z i z_i ,对于答案的贡献也是 0 0 。 0 0 时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【递推/dfs】牛的语言学
https://www.acwing.com/problem/content/description/5559/
题意:已知一个字符串由前段的一个词根和后段的多个词缀组成。词根的要求是长度至少为 5,词缀的要求是长度要么是 2, 要么是 3,以及不允许连续的相同词缀组成后段。现在给定最终的字符串,问一共有多少种词缀?按照字典序输出所有可能的词缀
思路一:搜索。很显然我们应该从字符串的最后开始枚举词缀进行搜索,因为词缀前面的所有字符全部都可以作为词根合法存在,我们只需要考虑当前划分出来的词缀是否合法即可。约束只有一个,不能与后面划分出来的词缀相同即可,由于我们是从后往前搜索,因此我们在搜索时保留后一个词缀即可。如果当前词缀和上一个词缀相同则返回,反之如果合法则加入 set 自动进行字典序排序。
时间复杂度:
O ( 2 n 2 ) O(2^{\frac{n}{2}}) 思路二:动态规划(递推)。动规其实就是 dfs 的逆过程,我们从已知结果判断当前局面是否合法。很显然词根是包罗万象的,只要长度合法,不管什么样的都是可行的,故我们在判断当前局面是否合法时,只需要判断当前词缀是否合法即可。于是便可知当前状态是从后面的字符串转移过来的。我们定义状态转移记忆数组
f[i]表示字符串s[1,i]是否可以组成词根。如果f[i]为真,则表示s[1,i]为一个合法的词根,s[i+1,n]为一个合法的词缀串,那么词根后面紧跟着的一定是一个长度为 2 或 3 的合法词缀。
我们以紧跟着长度为 2 的合法词缀为例。如果
s[i+1,i+2]为一个合法的词缀,则必须要满足以下两个条件之一
s[i+1,i+2]与s[i+3,i+4]不相等,即后面的后面是一个长度也为 2 且合法的词缀s[1,i+5]是一个合法的词根,即f[i+5]标记为真,即后面的后面是一个长度为 3 且合法的词缀以紧跟着长度为 3 的哈法词缀同理。如果
s[i+1,i+3]为一个合法的词缀,则必须要满足以下两个条件之一
s[i+1,i+3]与s[i+4,i+6]不相等,即后面的后面是一个长度也为 3 且合法的词缀s[1,i+5]是一个合法的词根,即f[i+5]标记为真,即后面的后面是一个长度为 2 且合法的词缀时间复杂度:
- O ( n log n ) O(n \log n) dp的过程是线性的,主要时间开销在set的自动排序上
dfs 代码
1 | |
dp 代码
1 | |
【线性dp】最小化网络并发线程分配
https://vijos.org/d/nnu_contest/p/1492
题意:现在有一个线性网络需要分配并发线程,每一个网络有一个权重,现在有一个线程分配规则。对于当前网络,如果权重比相邻的网络大,则线程就必须比相邻的网络大。
思路:我们从答案角度来看,对于一个网络,我们想知道它的相邻的左边线程数和右边线程数,如果当前网络比左边和右边的权重都大,则就是左右线程数的最大值+1,当然这些的前提是左右线程数已经是最优的状态,因此我们要先求“左右线程”。分析可知,左线程只取决于左边的权重与线程数,右线程同样只取决于右边的权重和线程数,因此我们可以双向扫描一遍即可求得“左右线程”。最后根据“左右线程”即可求得每一个点的最优状态。
1 | |
【线性dp】Block Sequence
https://codeforces.com/contest/1881/problem/E
题意:给定一个长为
的数组 a,问最少可以删除其中的几个元素,使得最终的数组可以被划分为连续的子数组且每一个子数组的元素个数均为「子数组首元素数值 n ≤ 2 × 1 0 5 n\le 2\times 10^5 」的形式。 − 1 -1 思路:
- 首先可以看出,序列的首元素一定是对应子数组剩余元素的个数。我们不妨倒序枚举每一个元素并定义
f[i]表示使数组a[i:]符合定义的最小删除次数,这样每次枚举到的元素都一定是所在子数组的首元素。- 接下来考虑状态转移。对于当前枚举到的元素
a[i],如果不删除,则f[i]将从f[i+a[i]+1]转移过来;如果删除,则f[i]将从f[i+1]转移过来。两者取最小值即可。时间复杂度
O ( n ) O(n)
1 | |
【线性dp】覆盖墙壁
https://www.luogu.com.cn/problem/P1990
题意:给定两种砖块,分别为日字型与L型,问铺满
的地板一共有多少种铺法 2 ∗ n 2*n 思路:
- 我们采用递推的思路
d e f i n e : define: f[i]表示铺满前个地板的方案数, 2 ∗ i 2*i g[i]表示铺满前块地板的方案数 2 ∗ i + 1 2*i+1 b a s e : base: f[0] = 1, f[1] = 1, g[0] = 0, g[1] = 1d p : dp: f[i] = f[i-1] + f[i-2] + g[i-1]∣ ∣ || g[i] = f[i-1] + g[i-1]r e s u l t : result: f[n]手绘:
1 | |
【线性dp】施咒的最大总伤害
https://leetcode.cn/problems/maximum-total-damage-with-spell-casting/
标签:线性 dp
题意:给定一个数组,选择一个子序列使得总和最大。约束为:如果选择了值为
的元素,则不允许选择值为 x x 的元素 x − 2 , x − 1 , x + 1 , x + 2 x-2,x-1,x+1,x+2 思路:
- 哈希计数。首先很显然的我们需要进行哈希计数,便于按数值升序枚举元素。我们定义哈希后的序列为
v,大小为m,存储每一种数的数值val: int和个数cnt: int- 状态定义。我们定义状态
f[i]表示哈希序列[1,i]中子序列总和的最大值,则最终答案就是f[m]- 状态转移。对于每一个哈希元素,都有选择和不选两种状态。假设当前枚举到的哈希元素为
i,
- 不选当前元素。就相当于没有当前元素,则
f[i] = f[i-1]- 选择当前元素。我们就需要从哈希序列
[1,i-1]中,比当前哈希元素v[i].val小 2 且对应子序列之和最大的那个状态f[j]转移过来。显然我们可以直接枚举哈希序列[1,i-1],但是这样就是必然超时,考虑优化。不难发现 O ( n 2 ) O(n^2) f[]数组是单调递增的并且哈希序列的元素数值v[].val也是单调递增的。也就是说对于当前状态f[i],在枚举哈希序列[1,i-1]时,其实并不需要从1开始枚举,可以从上一个状态枚举到的状态(记作j)开始枚举(因为上一个状态对应的f[j]是上一个状态可转移的方案中最大的并且v[j].val一定比当前方案的哈希数值v[i].val小 2)。于是状态转移的时间开销就从优化到 O ( n ) O(n) ,可以通过此题 O ( 1 ) O(1) 时间复杂度:
O ( n ) O(n) 空间复杂度:
O ( n ) O(n)
1 | |
1 | |
【线性dp】奇怪的汉诺塔
https://www.acwing.com/problem/content/98/
题意:四塔汉诺塔问题。求在给定
个圆盘的情况下的最少移动方案数。 n n 思路:
我们定义「最小完成单元」为:在满足游戏规则的情况下,将一座塔的所有圆盘移动到另一座塔所需的最少塔数。那么显然的最小完成单元为 3 座塔。定义
d[i]表示三塔模式下个盘的最少移动次数, i i f[i]表示四塔模式下个盘的最少移动次数。 i i 对于 4 座塔的情况,相当于最小完成单元又多了 1 座塔。那么显然多出来的这座塔有两个处置方案:
如果我们不利用这座塔。那么还剩 3 座塔,也就是最小完成单元,此时的最少移动次数是唯一的,也就是
f[i] = d[i]如果我们要利用这座塔。那么我们只能在这一座塔上按规则放圆盘。因为要确保最小完成单元来让剩余的圆盘移动到另一座塔。如果还在别的塔上放置了圆盘,那么将不符合最小完成单元的定义,游戏无法结束。当然我们不能将所有的圆盘都先放到这座塔上,因为这种情况下是不可能成立的,我们不可能让一个「我们正在求解的问题」作为我们的答案。也就是说
j < i j<i 至此四塔模式下
个圆盘游戏方案的组成集合已全部确定,如下图所示,即:在四塔模式下移动 i i 个圆盘到其中一座空塔上,方案数为 j ∈ [ 0 , i − 1 ] j \in [0,i-1] ;剩余的 f [ j ] f[j] 个圆盘处于最小完成单元的局面,方案数是唯一的 i − j i-j ;最后再将一开始移动的 d [ i − j ] d[i-j] 个圆盘在四塔模式下移动到刚才剩余圆盘移动到的塔上,方案数为 j j 。 f [ j ] f[j]
于是最终的状态转移方程为:
f i = min { f j + d i − j + f j } , i ∈ [ 1 , n ] , j ∈ [ 0 , i − 1 ] f_i = \min{ \{ f_j+d_{i-j}+f_j \} },\quad i \in [1,n],\quad j \in [0,i-1] 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【线性dp/dfs】数的计算
https://www.luogu.com.cn/problem/P1028
题意:给定一个数和一种构造方法,即对于当前的数,可以在其后面添加一个最大为当前一半大的数,以此类推构造成一个数列。问一共可以构造出多少个这种数列
思路一:dfs
- 非常显然的一个搜索树,答案就是结点数
- 时间复杂度:
O ( 方案数 ) O(\text{方案数}) 思路二:dp
非常显然的一个dp,我们定义一个dp记忆数组。其中
dp[i]表示数字i的构造方案总数,那么状态转移方程就是
d p [ i ] = ∑ j = 1 ⌊ i / 2 ⌋ d p [ j ] + 1 dp[i]=\sum_{j=1}^{\left\lfloor i/2 \right\rfloor}dp[j]+1 时间复杂度:
O ( n 2 ) O(n^2)
dfs代码
1 | |
dp代码
1 | |
【线性dp/二分答案】规划兼职工作
https://leetcode.cn/problems/maximum-profit-in-job-scheduling/description/
题意:给定 n 份工作的起始时间、终止时间、收益值,现在需要不重叠时间的选择工作使得收益最大
思路:动态规划、二分答案。为了不重不漏的枚举每一份工作,我们将工作按照结束时间进行排序,然后就可以枚举每一份工作了。接下来要解决的问题是,如何根据起始时间和终止时间进行工作的选择。显然的,每一份工作有选与不选两种状态,是否选择取决于收益是否更优,我们考虑动态规划。我们定义状态表
f[i]表示在前 i 个工作中选择的最大工作收益,返回值就是f[n],先看图
- 选择第 i 个工作:
f[i] = f[r] + profit[i](其中 r 表示[1,i-1]份工作中,结束时间早于当前工作起始时间的最右边的工作,在[1,i-1]中二分查找即可)- 不选第 i 个工作:
f[i] = f[i - 1]选择最大属性进行状态转移即可:
f[i] = max(f[i - 1], f[r] + profit[i])时间复杂度:
O ( n log n ) O(n\log n)
1 | |
【线性dp/二分查找】最长上升子序列
https://www.luogu.com.cn/problem/B3637
题意:给定序列,求解其中最长上升子序列 (Longest Increasing Subsequence, 简称 LIS) 的长度。
思路:我们采用动态规划。
状态定义:定义状态数组
f[i]表示以元素a[i]结尾的最长上升子序列的长度,显然的初始状态全都是1状态转移:
暴力枚举。首先很显然的
f[i]一定是从[0,i-1]中比当前元素值小的状态转移过来,于是可以很轻松的写出双重循环的代码,时间复杂度。 O ( n 2 ) O(n^2) 贪心+二分优化。
回顾朴素。优化需要在理解转移本质的基础上展开,因此我们先来回顾一下朴素版的转移方案:从
[0,i-1]中比当前元素小的元素a[j]对应的最长上升子序列长度f[j]转移过来。我们枚举了[0,i-1]所有的状态确保了不重不漏。对于i = 6来说,如下图所示。其中✔表示进入了if的判断逻辑。最终我们选择从j = 5对应的f[j] = 3转移而来。这里的判断准则为:对于每一个元素,需要找前面的元素中比当前元素小的元素。
转换视角。同样对于每一个元素
a[i],我们不再按顺序枚举前面已经计算出来的f[1:i-1],而是预先按照长度存储所有的f[1:i-1]从而枚举长度j,显然可以贪心的从最大长度mxa_len开始枚举。一旦遇到比a[i]小的元素,那么f[i]就等于当前枚举的长度+1,即f[i] = j + 1。对于i = 6来说,如下图所示。这样也可以做到不重不漏的枚举所有状态。但是显然的,这种方法只是变相地枚举了所有的元素,仍然是,并且和枚举元素相比还多了一点思维量和代码量。 O ( n 2 ) O(n^2)
优化诞生。在枚举元素时,并没有额外有价值的信息,比如元素并非单调排列,
f[]数组也并非单调。但转换到枚举长度,让我们有机会进行优化!不难发现,对于每一个元素a[i],我们在按长度[1,max_len]枚举可能的尾元素f[1:i-1]时,由于max_len每一次更新时的增量都是 1,因此[1,max_len]的每一个取值都一定会有对应的元素存在!贪心的,对于同一个长度下所有子序列的尾元素,我们只关心其中值最小的那一个尾元素,因此我们定义一个mi[]数组来存储每一个长度下子序列尾元素的最小值,其中mi[i]表示长度为i的最长上升子序列中,最小的尾元素值。这样在枚举长度[1,max_len]时,就不再需要枚举每一个长度下所有的尾元素,仅需枚举每一个长度下唯一的那个最小尾元素。但如果每一个长度都刚好只有一个元素,那岂不是还是需要线性枚举?更进一步的,我们可以发现,此时每一个长度对应的唯一元素组成的序列是严格单调递增的(反证法易证)!有了这样单调的性质我们就可以利用二分加速枚举,这样可以将枚举的时间复杂度严格控制在。显然的,我们希望当前的元素可以拼接在尽可能长的子序列后面,因此此处的二分使用的是寻找右边界的板子。 O ( log n ) O(\log n)
代码实现。枚举每一个元素肯定是少不了的,我们使用
mi[j]表示最长上升子序列长度为j的序列尾元素的最小值。初始状态显然就是mi[1] = a[0]。在每一个元素二分查询「最大的比当前元素小的元素」时,如果查出来的元素mi[r]确实比当前元素小,则需要更新mi[r+1]的值;反之如果查出来的元素mi[r]比当前元素还小,则表明二分到了左边界,此时r一定是 1,直接用当前元素覆盖mi[1]即可。答案表示。最终答案就是
max_len时间复杂度:
O ( n log n ) O(n \log n)
暴力枚举元素
1 | |
暴力枚举长度
1 | |
贪心二分优化
1 | |
【网格图dp/dfs】过河卒
https://www.luogu.com.cn/problem/P1002
题意:给定一个矩阵,现在需要从左上角走到右下角,问一共有多少种走法?有一个特殊限制是,对于图中的9个点是无法通过的。
思路一:dfs
我们可以采用深搜的方法。但是会超时,我们可以这样估算时间复杂度:对于每一个点,我们都需要计算当前点的右下角的矩阵中的每一个点,那么总运算次数就近似为阶乘级别。当然实际的时间复杂度不会这么大,但是这种做法
一旦超过100就很容易tle n ∗ m n*m 时间复杂度:
O ( n m ! ) O(nm!) 思路二:dp
我们可以考虑,对于当前的点,可以从哪些点走过来,很显然就是上面一个点和左边一个点,而对于走到当前这个点的路线就是走到上面的点和左边的点的路线之和,base状态就是
dp[1][1] = 1,即起点的路线数为1时间复杂度:
O ( n m ) O(nm)
dfs代码
1 | |
dp代码
1 | |
【网格图dp】摘樱桃 II
https://leetcode.cn/problems/cherry-pickup-ii/
题意:给定一个
行 n n 列的网格图,每个格子拥有一个价值。现在有两个人分别从左上角和右上角开始移动,移动方式为「左下、下、右下」三个方向,问两人最终最多一共可以获得多少价值?如果两人同时经过一个位置,则只能算一次价值。 m m 思路:
状态定义。最终状态一定是两人都在最后一行的任意两列,我们如何定义状态可以不重不漏的表示两人的运动状态呢?可以发现两人始终在同一行,但是列数不一定相同,我们定义状态
表示两人走到第 f [ i ] [ j ] [ k ] f[i][j][k] 行时,一人在第 i i 列,另一人在第 j j 列时的总价值。则答案就是: k k
max ( f [ n − 1 ] [ j ] [ k ] ) , j , k ∈ [ 0 , m ] \max{(f[n-1][j][k])},j,k\in[0,m] 状态转移。本题难点在于状态定义,一旦定义好了以后状态转移就不困难了。对于当前状态
,根据乘法原理,两人均有 3 种走法,因此当前状态可以从 f [ i ] [ j ] [ k ] f[i][j][k] 种合法状态转移过来。取最大值即可。 3 × 3 = 9 3\times 3=9 时间复杂度:
O ( n m 2 ) O(nm^2)
1 | |
【网格图dp】摘樱桃
弱化版
强化版
题意:给定一个 n 行 n 列的网格图,问从左上走到右下,再从右下走到左上最多可以获得多少价值?一个单元格只能被计算一次价值。
注:弱化版中 -1 表示不可达,强化版没有不可达的约束。强化版 AC 代码
思路一:暴力dp
- 首先对于来回问题可以转化为两次去的问题,即问题等价于求解「两个人从左上角走到右下角」的最大收益。
- 显然我们可以定义四维的状态,其中
表示第一个人走到 f [ i ] [ j ] [ p ] [ q ] f[i][j][p][q] 且第二个人走到 ( i , j ) (i,j) 时的最大收益。直接枚举这四个维度,然后从 4 个合法的子问题转移过来即可。 ( p , q ) (p,q) - 时间复杂度:
O ( n 4 ) O(n^4) 思路二:优化dp
- 注意到问题可以进一步等价于「两个人同时从左上角走到右下角」的最大收益。也就是两个人到起点
的曼哈顿距离应该是一样的,即 ( 0 , 0 ) (0,0) ,也就是说如果其中一个人 i + j = p + q i+j=p+q 的位置确定了,则另一个人只需要枚举一个下标,另一个下标就可以 ( i , j ) (i,j) 的确定了。可以将时间复杂度降低一个维度。 O ( 1 ) O(1) - 状态定义。我们定义
表示第一个人走到 f [ k ] [ i 1 ] [ i 2 ] f[k][i_1][i_2] 且第二个人走到 ( i 1 , k − i 1 ) (i_1,k-i_1) 时的最大收益。则最终答案就是 ( i 2 , k − i 2 ) (i_2,k-i_2) 。状态转移同理,从 4 个合法子问题转移过来即可。 f [ 2 n − 2 ] [ n − 1 ] [ n − 1 ] f[2n-2][n-1][n-1] - 时间复杂度:
O ( n 3 ) O(n^3)
暴力dp:
1 | |
优化dp:
1 | |
【树形dp】最大社交深度和
https://vijos.org/d/nnu_contest/p/1534
算法:树形dp、BFS
题意:给定一棵树,现在需要选择其中的一个结点为根节点,使得深度和最大。深度的定义是以每个结点到树根所经历的结点数
思路一:暴力
显然可以直接遍历每一个结点,计算每个结点的深度和,然后取最大值即可
时间复杂度:
O ( n 2 ) O(n^2) 思路二:树形dp
我们可以发现,对于当前的根结点
fa,我们选择其中的一个子结点ch,将ch作为新的根结点(如右图)。那么对于当前的ch的深度和,我们可以借助fa的深度和进行求解。我们假设以ch为子树的结点总数为x,那么这x个结点在换根之后,相对于ch的深度和,贡献了-x的深度;而对于fa的剩下来的n-x个结点,相对于ch的深度和,贡献了n-x的深度。于是ch的深度和就是fa的深度和-x+n-x,即:
d e p [ c h ] = d e p [ f a ] − x + n − x = d e p [ f a ] + n − 2 × x dep[ch] = dep[fa]-x+n-x = dep[fa]+n-2\times x 于是我们很快就能想到利用前后层的递推关系,
的计算出所有子结点的深度和。 O ( 1 ) O(1) 代码实现:我们可以先计算出
base的情况,即任选一个结点作为根结点,然后基于此进行迭代计算。在迭代计算的时候需要注意的点就是在一遍dfs计算某个结点的深度和dep[root]时,如果希望同时计算出每一个结点作为子树时,子树的结点数,显然需要分治计算一波。关于分治的计算我熟练度不够高,特此标注一下debug了3h的点:即在递归到最底层,进行回溯计算的时候,需要注意不能统计父结点的结点值(因为建的是双向图,所以一定会有从父结点回溯的情况),那么为了避开这个点,就需要在的时间复杂度内获得当前结点的父结点的编号,从而进行特判,采用的方式就是增加递归参数 O ( 1 ) O(1) fa。没有考虑从父结点回溯的情况的dfs代码
2
3
4
5
6
7
8
9
10void dfs(int now, int depth) {
if (!st[now]) {
st[now] = true;
dep[root] += depth;
for (auto& ch: G[now]) {
dfs(ch, depth + 1);
cnt[now] += cnt[ch];
}
}
}考虑了从父结点回溯的情况的dfs代码
2
3
4
5
6
7
8
9
10
11
12void dfs(int now, int fa, int depth) {
if (!st[now]) {
st[now] = true;
dep[root] += depth;
for (auto& ch: G[now]) {
dfs(ch, now, depth + 1);
if (ch != fa) {
cnt[now] += cnt[ch];
}
}
}
}时间复杂度:
Θ ( 2 n ) \Theta(2n)
暴力代码:
1 | |
优化代码:
1 | |
【高维dp/dfs】栈
https://www.luogu.com.cn/problem/P1044
题意:n个数依次进栈,随机出栈,问一共有多少种出栈序列?
思路一:dfs
- 我们可以这么构造搜索树:已知对于当前的栈,一共有两种状态
- 入栈 - 如果当前还有数没有入栈
- 出栈 - 如果当前栈内还有元素
- 搜索参数:
i,j表示入栈数为i出栈数为j的状态- 搜索终止条件
- 入栈数 < 出栈数 -
i < j i<j - 入栈数 > 总数
- n n i = n i = n - 答案状态:入栈数为n,出栈数也为n
- 时间复杂度:
O ( 方案数 ) O(\text{方案数}) 思路二:dp
采用上述dfs时的状态表示方法,
i,j表示入栈数为i出栈数为j的状态。我们在搜索的时候,考虑的是接下来可以搜索的状态
即出栈一个数的状态 -
i+1,j和入栈一个数的状态 -
i,j+1如图:
而我们在dp的时候,需要考虑的是子结构的解来得出当前状态的答案,就需要考虑之前的状态。即当前状态是从之前的哪些状态转移过来的。和上述dfs思路是相反的。我们需要考虑的是
- 上一个状态入栈一个数到当前状态 -
i-1,j→ \to i,j- 上一个状态出栈一个数到当前状态 -
i,j-1→ \to i,j
- 特例:
时,只能是上述第二种状态转移而来,因为要始终保证入栈数大于等于出栈数,即 i = j i=j i ≥ j i \ge j 如图:
我们知道,入栈数一定是大于等于出栈数的,即
。于是我们在枚举 i ≥ j i\ge j 的时候,枚举的范围是 j j [ 1 , i ] [1,i]
状态的构建取决于 b a s e base 时的所有状态,我们知道没有任何数出栈也是一种状态,于是 j = 0 j=0
d p [ i ] [ 0 ] = 0 , ( i = 1 , 2 , 3 , . . . , n ) dp[i][0]=0,(i=1,2,3,...,n) 时间复杂度:
O ( n 2 ) O(n^2)
dfs代码
1 | |
dp代码
1 | |
【高维dp】找出所有稳定的二进制数组 II
https://leetcode.cn/problems/find-all-possible-stable-binary-arrays-ii/
题意:构造一个仅含有
个 n n , 0 0 个 m m 的数组,且长度超过 1 1 的子数组必须同时含有 k k 和 0 0 。给出构造的总方案数对 1 1 取余后的结果。 1 0 9 + 7 10^9+7 思路:
定义状态表。我们从左到右确定每一位的数字时,需要确定这么三个信息:当前是哪一位?还剩几个
和 0 0 ?这一位填 1 1 还是 0 0 ?对于这三个信息,我们可以定义状态数组 1 1 表示当前已经选了 f [ i ] [ j ] [ k ] f[i][j][k] 个 i i , 0 0 个 j j ,且第 1 1 位填 i + j i+j 时的方案数。这样最终答案就是 k k 。 f [ n ] [ m ] [ 0 ] + f [ n ] [ m ] [ 1 ] f[n][m][0]+f[n][m][1] 定义子问题。以当前第
位填 i + j i+j 为例,填 0 0 同理,即当前需要维护的是 1 1 。显然的如果前一位是和当前位不同,即 f [ i ] [ j ] [ 0 ] f[i][j][0] 时,可以直接转移过来;如果前一位和当前位相同,即 1 1 时,有可能会出现长度超过 0 0 的连续 k k 子数组,即前段数组刚好是以「一个 0 0 和 1 1 个 k k 结尾的」合法数组,此时再拼接一个 0 0 就不合法了。 0 0 状态转移方程。综上所述,可以得到以下两个状态转移方程:
f [ i ] [ j ] [ 0 ] = f [ i − 1 ] [ j ] [ 1 ] + f [ i − 1 ] [ j ] [ 0 ] − f [ i − k − 1 ] [ j ] [ 1 ] f [ i ] [ j ] [ 1 ] = f [ i ] [ j − 1 ] [ 0 ] + f [ i ] [ j − 1 ] [ 1 ] − f [ i ] [ j − k − 1 ] [ 0 ] \begin{aligned}f[i][j][0] = f[i - 1][j][1] + f[i - 1][j][0] - f[i - k - 1][j][1] \\f[i][j][1] = f[i][j - 1][0] + f[i][j - 1][1] - f[i][j - k - 1][0]\end{aligned} 时间复杂度:
O ( n m ) O(nm)
1 | |
【高维dp】学生出勤记录 II
https://leetcode.cn/problems/student-attendance-record-ii/description/
题意:构造一个仅含有
三种字符的字符串,使得 P , A , L P,A,L 最多出现 A A 次,同时 1 1 最多连续出现 L L 次。问一共有多少种构造方案?对 2 2 取模。 1 0 9 + 7 10^9+7 思路:
- 模拟分析问题。我们从前往后构造。对于当前第
个字符 i i ,有 s [ i ] s[i] 种可能的选项,其中 3 3 是一定合法的选项, P P 是否合法取决于 A A 中的 s [ 0 : i − 1 ] s[0:i-1] 的数量, A A 是否合法取决于 L L 的末尾连续 s [ 0 : i − 1 ] s[0:i-1] 的数量。因此我们可以通过被动转移的动态规划求解。 L L - 状态定义。从上述分析不难发现需要
种状态来表示所有情况,因此我们定义 3 3 表示构造第 f [ i ] [ j ] [ k ] f[i][j][k] 位时, i i 中含有 s [ 0 : i ] s[0:i] 个 j j 且末尾含有连续 A A 个 k k 时的方案数。 L L - 初始化。每一位填什么取决于前缀
的情况,因此我们需要初始化 s [ 0 : i − 1 ] s[0:i-1] 即第 f [ 0 ] [ ] [ ] f[0][][] 位的情况。显然的第 0 0 位 0 0 三种都可以填,对应的就是 P , A , L P,A,L ,其余初始化为 f [ 0 ] [ 0 ] [ 0 ] = f [ 0 ] [ 1 ] [ 0 ] = f [ 0 ] [ 0 ] [ 1 ] = 1 f[0][0][0] = f[0][1][0] = f[0][0][1] = 1 即可。 0 0 - 状态转移。考虑第
位的三种情况: i i
- 填
:可以用前缀的所有状态来更新 P P f [ i ] [ j ] [ 0 ] f[i][j][0] - 填
:可以用前缀中不含 A A 的所有状态来更新 A A f [ i ] [ 1 ] [ 0 ] f[i][1][0] - 填
:可以用前缀中末尾不超过 L L 位 1 1 的所有状态来更新 L L f [ i ] [ j ] [ k ] f[i][j][k] - 最终答案。为
。 ∑ j = 0 1 ∑ k = 0 2 f [ n − 1 ] [ j ] [ k ] \displaystyle \sum_{j=0}^{1}\sum_{k=0}^{2}f[n-1][j][k] 时间复杂度:
Θ ( 6 n ) \Theta (6n)
1 | |
1 | |
【区间dp】对称山脉
https://www.acwing.com/problem/content/5169/
模拟,时间复杂度
1 | |
dp优化,时间复杂度
1 | |
【状压dp】Avoid K Palindrome 🔥
https://atcoder.jp/contests/abc359/tasks/abc359_d
题意:给定一个长度为
的字符串 n ≤ 1000 n\le 1000 和一个整数 s s ,其中含有若干个 k ≤ 10 k\le10 'A','B'和'?'。其中'?'可以转化为'A'或'B',假设有和 q q '?',则一共可以转化出个不同的 2 q 2^q 。问所有转化出的 s s 中,有多少是不含有长度为 s s 的回文子串的。 k k 思路:最暴力的做法就是 2^q 枚举所有可能的字符串,然后再 O(n) 的检查,这样时间复杂度为
,只能通过 20 以内的数据。一般字符串回文问题可以考虑 dp。 O ( n 2 n ) O(n2^n) 时间复杂度:
1 | |
数据结构由 数据 和 结构 两部分组成。我们主要讨论的是后者,即结构部分。
按照 逻辑结构 可以将其区分为 线性结构 和 非线性结构。

按照 物理结构 可以将其区分为 连续结构 和 分散结构。

【模板】双链表
https://www.acwing.com/problem/content/829/
思路:用两个空结点作为起始状态的边界,避免所有边界讨论。
时间复杂度:插入、删除结点均为
,遍历为 O ( 1 ) O(1) O ( n ) O(n)
1 | |
1 | |
【模板】单调栈
https://www.acwing.com/problem/content/832/
题意:对于一个序列中的每一个元素,寻找每一个元素左侧最近的比其小的元素。
思路一:暴力枚举
- 显然对于每一个元素
nums[i],我们可以枚举倒序[0, i-1]直到找到第一个nums[j] < nums[i]- 时间复杂度:
O ( n 2 ) O(n^2) 思路二:单调栈
可以发现时间开销主要在倒序枚举上,我们能少枚举一些元素吗?答案是可以的。我们定义「寻找
[i-1, 0]中比当前元素小的第一个元素」的行为叫做「寻找合法对象」。显然我们在枚举每一个元素时都需要 查询 和 维护 这样的合法对象线性序列,可以理解为记忆化从而加速查询。那么如何高效查询和维护这样的线性序列呢?不妨考虑每一个合法对象对曾经的合法对象的影响:
- 若当前元素
nums[i]可以成为后续[i+1, n-1]元素的合法对象。则从i-1开始一直往左,只要比当前大的元素,都不可能成为[i+1, n-1]的合法对象,肯定都被nums[i]“拦住了”。那么在「合法对象序列」中插入当前合法对象之前,需要不断尾弹出比当前大的元素- 若当前元素
nums[i]不能成为后续[i+1, n-1]元素的合法对象。表明当前元素过大,此时就不用将当前元素插入「合法对象序列」经过上述两个角度的讨论,很容易发现这样维护出来的的合法序列是严格单调递增的。于是,在查询操作时仅需要进行尾比较与尾弹出即可,在维护操作时,仅需要尾插入即可。满足这样的线性数据结构有很多,如栈、队列、数组、链表,我们就使用栈来演示,与标题遥相呼应
时间复杂度:
O ( n ) O(n)
1 | |
相似题:
【模板】单调队列
标签:双端队列、滑动窗口、单调队列
题意:给定一个含有 n 个元素的序列,求解其中每个长度为 k 的子数组中的最值。
思路:显然我们可以
暴力求解,有没有什么方法可以将「求解子数组中最值」的时间开销从 O ( n k ) O(nk) 降低为 O ( k ) O(k) 呢?有的!我们重新定义一个队列就好了。为了做到线性时间复杂度的优化,我们对队列做以下自定义,以「求解子数组最小值」为例: O ( 1 ) O(1)
- 插入元素到队尾:此时和单调栈的逻辑类似。如果当前元素可以作为当前子数组或后续子数组的最小值,则需要从当前队尾开始依次弹出比当前元素严格大的元素,最后再将当前元素入队。注意:当遇到和当前元素值相等的元素时不能出队,因为每一个元素都会经历入队和出队的操作,一旦此时出队了,后续进行出队判定时会提前弹出本不应该出队的与其等值的元素。
- 弹出队头元素:如果队头元素和子数组左端点
nums[i-k]的元素值相等,则弹出。- 获得队头元素:
的获取队头元素,即队列中的最小值。 O ( 1 ) O(1) 时间复杂度:
O ( n ) O(n)
1 | |
1 | |
【模板】最近公共祖先
https://www.luogu.com.cn/problem/P3379
题意:寻找树中指定两个结点的最近公共祖先
。 (Lowest Common Ancestor, 简称 LCA) \text{(Lowest Common Ancestor, 简称 LCA)} 思路:对于每次查询,我们可以从指定的两个结点开始往上跳,第一个公共结点就是目标的 LCA,每一次询问的时间复杂度均为
,为了加速查询,我们可以采用倍增法,预处理出往上跳的结果,即 O ( n ) O(n) fa[i][j]数组,表示号点向上跳 i i 步后到达的结点。接下来在往上跳跃的过程中,利用二进制拼凑的思路,即可在 2 j 2^j 的时间内查询到 LCA。 O ( log n ) O(\log n) 预处理:可以发现,对于
fa[i][j],我们可以通过递推的方式获得,即fa[i][j] = fa[fa[i][j-1]][j-1],当前结点向上跳跃步可以拆分为先向上 2 j 2^j 步, 在此基础之上再向上 2 j − 1 2^{j-1} 步.于是我们可以采用宽搜 2 j − 1 2^{j-1} 深搜的顺序维护 o r or 数组。 f a fa 跳跃:我们首先需要将两个结点按照倍增的思路向上跳到同一个深度,接下来两个结点同时按照倍增的思路向上跳跃,为了确保求出最近的,我们需要确保在跳跃的步调一致的情况下,两者的祖先始终不相同,那么倍增结束后,两者的父结点就是最近公共祖先,即
fa[x][k]或fa[y][k]时间复杂度:
Θ ( n log n + m log n ) \Theta(n \log n + m \log n)
为预处理每一个结点向上跳跃抵达的情况 n log n n \log n 为 m log n m \log n 次询问的情况 m m
1 | |
【栈】验证栈序列
https://www.luogu.com.cn/problem/P4387
题意:给定入栈序列与出栈序列,问出栈序列是否合法
思路:思路很简单,就是对于当前出栈的数,和入栈序列中最后已出栈的数之间,如果还有数没有出,那么就是不合法的出栈序列,反之合法。这是从入栈的结果来看的,如果这么判断就需要扫描入栈序列 n 次,时间复杂度为
。我们按照入栈的顺序来看,对于当前待入栈的数,若与出栈序列的队头不等,则成功入栈等待后续出栈;若与出栈序列相等,则匹配成功直接出栈无需入栈,同时对已入栈的数与出栈序列队头不断匹配直到不相等。最后判断待入栈的数与出栈序列是否全部匹配掉了,如果全部匹配掉了说明该出栈序列合法,反之不合法 O ( n 2 ) O(n^2) 抽象总结上述思路:为了判断出栈序列是否合法,我们不妨思考:对于每一个出栈的数,出栈的时机是什么?可以发现出栈的时机无非两种:
- 一入栈就出栈(对应于枚举待入栈序列时发现待入栈的数与出栈序列队头相等)
- 紧跟着刚出栈的数继续出栈(对应于枚举待入栈序列时发现待入栈的数与出栈序列队头相等之后,继续判断出栈序列队头与已入栈的数是否相等,若相等则不断判断并出栈)
时间复杂度:
O ( n ) O(n)
1 | |
二叉搜索树 & 平衡树
如果我们想要在
关于平衡二叉搜索树,有非常多的变种与实现,不同的应用场景会选择不同的平衡树类型。Treap 更灵活,通过随机化优先级实现预期的平衡,但在最坏情况下可能退化。AVL 树 严格保持平衡,保证了 map 和 set)。一般来说,红黑树是一个较为通用的选择,而在需要严格平衡性时,AVL 树可能是更好的选择。
Treap
Treap 是二叉搜索树和堆的结合体。它通过维护两种性质来保持平衡:
- 二叉搜索树性质:每个节点的左子树的所有节点值小于该节点的值,右子树的所有节点值大于该节点的值。
- 堆性质:每个节点的优先级(通常随机生成)要大于或等于其子节点的优先级。
平衡机制:
- Treap 使用随机化优先级使得树的形状接近于理想的平衡树(期望树高为
)。 O ( log n ) O(\log n) - 通过旋转操作(左旋和右旋)在插入和删除时保持堆的性质。
优点:
- 实现相对简单。
- 由于随机化的优先级,在期望情况下,树的高度是
。 O ( log n ) O(\log n) - 灵活性高,可以根据需要调整优先级函数。
缺点:
- 最坏情况下,树的高度可能退化为
(例如所有优先级相同或顺序生成的优先级),尽管发生概率很低。 O ( n ) O(n)
AVL 树
AVL 树是最早发明的自平衡二叉搜索树之一,1962 年由 Adelson-Velsky 和 Landis 发明。
- 平衡因子:每个节点的左右子树高度差不能超过
,且需要记录每个节点的高度。 1 1 平衡机制:
- 插入或删除节点后,如果某个节点的平衡因子不再为
、 − 1 -1 或 0 0 ,就需要通过旋转(单旋转或双旋转)来恢复平衡。 1 1 - 旋转操作包括:左旋转、右旋转、左右双旋转和右左双旋转。
优点:
- 严格的平衡条件保证了树的高度始终为
,因此搜索、插入和删除操作的时间复杂度为 O ( log n ) O(\log n) 。 O ( log n ) O(\log n) 缺点:
- 由于平衡条件严格,每次插入和删除后可能需要较多的旋转操作,从而导致实现较复杂,插入和删除操作的常数时间开销较大。
红黑树
红黑树是一种较为宽松的自平衡二叉搜索树,由 Rudolf Bayer 于 1972 年发明。
- 颜色属性:每个节点都有红色或黑色两种颜色,通过这些颜色约束树的平衡性。
平衡机制:
- 通过遵循红黑树的五个性质来保持平衡:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 叶子节点(NIL 节点)是黑色。
- 如果一个节点是红色的,那么它的子节点必须是黑色(红节点不能连续出现)。
- 从任一节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。
- 插入和删除操作可能破坏红黑树的性质,需要通过重新着色和旋转来恢复平衡。
优点:
- 红黑树的高度最多是
,因此搜索、插入和删除操作的时间复杂度仍为 Θ ( 2 log n ) \Theta (2 \log n) 。 O ( log n ) O(\log n) - 由于平衡条件较为宽松,插入和删除操作需要的旋转操作通常比 AVL 树少,效率更高。
缺点:
- 实现较复杂,特别是插入和删除的平衡修复过程。
- 虽然红黑树的搜索效率与 AVL 树相似,但由于平衡条件较宽松,实际应用中的树高度通常略高于 AVL 树,因此搜索操作的效率稍低。
【二叉树】美国血统
https://www.luogu.com.cn/problem/P1827
题意:给定二叉树的中序和先序序列,输出后序序列
思路:经典二叉树的题目,主要用于巩固加强对于递归的理解。指针其实是没有必要的,为了得到后序序列,我们只需要有一个 dfs 序即可,为了得到 dfs 序,我们只需要根据给出的中序和前序序列即可得到 dfs 序
时间复杂度:
O ( n ) O(n)
指针做法
1 | |
构造出 dfs 序直接输出
1 | |
【二叉树】新二叉树
https://www.luogu.com.cn/problem/P1305
题意:给定一棵二叉树的 n 个结点信息,分别为当前结点的数据信息、左孩子结点信息和右结点信息,输出这棵二叉树的前序序列
思路:我们首先将这棵二叉树构建出来,接着遍历输出前序序列即可。关键在于如何构建二叉树?我们使用数组存储二叉树,对于每一个树上结点,我们将数组中元素的索引存储为树上结点信息,每一个结点再存储左孩子与右孩子的信息
时间复杂度:
O ( n ) O(n)
1 | |
【二叉树】遍历问题
https://www.luogu.com.cn/problem/P1229
题意:给定一棵二叉树的前序序列与后序序列,问中序序列的可能情况有多少种
思路:我们采用从最小结构单元的思路进行考虑,即假设当前二叉树只有一个根结点与两个叶子结点,而非两棵子树。然后将题意进行等价变换,即问对于已经固定的前序和后序二叉树,该二叉树有多少种不同的形状?对于当前的最小结构二叉树,形状就是 左右根 or 根左右,现在的根可以直接确定,那么就只能从左右孩子进行变形,很显然只能进行左右交换的变形,但是问题是一旦左右变换,前序 or 后序都会变掉,说明这种左右孩子都存在的前后序固定的二叉树是唯一的,那么如何才是不唯一的呢?我们考虑减少孩子数量。假设没有孩子,那么很显然也只有一个形状,就是一个根结点,故排除。于是答案就呼之欲出了,就是当根结点只有一个孩子时,这个孩子无论是在左边还是右边,前后序都是相同的,但是中序序列就不同了,于是就产生了两种中序序列。于是最终的结论是:对于前后序确定的二叉树来说,中序序列的情况是就是
个。现在的问题就转变为了在给定前后序的二叉树中求解单分支结点个数的问题。 2 单分支结点数 2^{\text{单分支结点数}} 如何寻找单分支结点呢?根据下面的递归图可以发现,无论是左单分支还是右单分支,如果 pre 的连续两个结点与 post 的连续两个结点对称相同,那么就一定有一个单分支结点,故只需要寻找前后序序列中连续两个字符对称相同的情况数 cnt 即可。最终的答案数就是
2 c n t 2^{cnt}
时间复杂度:
O ( n m ) O(nm)
1 | |
【二叉树】医院设置 🔥
https://www.luogu.com.cn/problem/P1364
题意:给定一棵二叉树,树中每一个结点存储了一个数值表示一个医院的人数,现在需要在所有的结点中将一个结点设置为医院使得其余结点中的所有人到达该医院走的路总和最小。路程为结点到医院的最短路,边权均为 1。给出最终的最短路径总和
思路一:暴力
显然的对于已经设置好医院的局面,需要求解的路径总和就直接将树遍历一边即可。每一个结点都可以作为医院进行枚举,每次遍历是
的 O ( n ) O(n) 时间复杂度:
O ( n 2 ) O(n^2) 思路二:带权树的重心
- TODO
- 时间复杂度:
O ( n ) O(n)
暴力代码
1 | |
优化代码
1 | |
【二叉树】二叉树深度
https://www.luogu.com.cn/problem/P4913
题意:给定一棵二叉树,求解这棵二叉树的深度
思路:有两个考点,一个是如何根据给定的信息(从根结点开始依次给出已存在树上结点的左右孩子的编号)构建二叉树,一个是如何求解已经构建好的二叉树的深度。对于构建二叉树,我们沿用 T5 数组模拟构建的思路,直接定义结点类型即可;对于求解深度,很显然的一个递归求解,即左右子树深度值 +1 即可
时间复杂度:
O ( n ) O(n)
1 | |
【完全二叉树】淘汰赛
https://www.luogu.com.cn/problem/P1364
题意:给定
支球队的编号与能力值,进行淘汰赛,能力值者晋级下一轮直到赛出冠军。输出亚军编号 2 n 2^n 思路:很显然的一个完全二叉树的题目。我们都不需要进行递归操作,直接利用完全二叉树的下标性质利用数组模拟循环计算即可。给出的信息就是完全二叉树的全部叶子结点的信息,分别为球队编号 id 与球队能力值 val,我们从第 n-1 个结点开始循环枚举到第 1 个结点计算每一轮的胜者信息,最终输出最后一场的能力值较小者球队编号即可
时间复杂度:
Θ ( 2 n ) \Theta(2n)
1 | |
【二叉树/LCA】二叉树问题
https://www.luogu.com.cn/problem/P3884
题意:给定一棵二叉树的结点关系信息,求出这棵二叉树的深度、宽度和两个指定结点之间的最短路径长度
思路:二叉树的构建直接采用有向图的构造方法。深度直接 dfs 即可,宽度直接在 dfs 遍历时哈希深度值即可。问题的关键在于如何求解两个给定结点之间的路径长度,很显然需要求解两个结点的 LCA,由于结点数
故直接采用暴力的方法,可以重定义结点,增加父结点域。也可以通过比对根结点到两个指定结点的路径信息得到 LCA 即最后一个相同的结点编号(本题采用),通过在 dfs 遍历树时存储路径即可得到根结点到两个指定结点的路径信息。之后直接根据题中新定义的路径长度输出即可,即 ≤ 100 \le 100
length = 2 × ( d x − d l c a ) + ( d y − d l c a ) \text{length} = 2 \times (d_x - d_{lca}) + (d_y - d_{lca}) 其中
表示:根结点到第 d i d_i 号点之间的路径长度,在 dfs 时通过传递深度值维护得到 i i 时间复杂度:
O ( n ) O(n)
1 | |
【set】营业额统计
https://www.luogu.com.cn/problem/P2234
题意:给定一个序列 a,需要计算
,即计算每一个数与序列中当前数之前的数的最小差值之和 a 1 + ∑ i = 2 , 1 ≤ j < i n min ∣ a i − a j ∣ a_1 + \displaystyle \sum_{i=2,1 \le j <i}^{n} \min {|a_i - a_j|} 思路:很显然的思路,对于每一个数,我们需要对之前的序列在短时间内找到一个数值最接近当前数的数。
- TLE:一开始的思路是每次对之前的序列进行排序,然后二分查找与当前值匹配的数,为了确保所有的情况都找到,就直接判断二分查到的数,查到的数之前的一个数,之后的一个数,但是时间复杂度极高(我居然没想到),是
O ( n 2 log n ) O(n^2 \log n) - AC:后来看了题解才知道
set的正确用法,就是一个 平衡树的 STL。我们对于之前的序列不断的插入平衡树中(默认升序排序),每次利用s.lower_bound(x)返回「集合s中第一个当前数的迭代器」,然后进行判断即可。 ≥ \ge lower_bound()的时间复杂度为。需要注意的是边界的判断,一开始的思路虽然会超时,但是二分后边界的判断很简单,使用 STL 后同样需要考虑边界的情况。分为三种(详情见代码) O ( log n ) O(\log n)
- 当前数比集合中所有的数都大,那么
lower_bound就会返回s.end()答案就是当前数与集合中最后一个数的差值- 当前数比集合中所有的数都小,那么
lower_bound就会返回s.bigin()答案就是集合中第一个数与当前数的差值- 当前数存在于集合中 or 集合中既有比当前数大的又有比当前数小的,那么就比较查到的数与查到的数前一个数和当前数的差值,取最小的差值即可
时间复杂度:
O ( n log n ) O(n \log n)
TLE 但逻辑清晰代码
1 | |
AC 的 set 代码
1 | |
【multiset】切蛋糕
https://www.acwing.com/problem/content/description/5581/
题意:给定一个矩形,由左下角和右上角的坐标确定。现在对这个矩形进行切割操作,要么竖着切,要么横着切。现在需要给出每次切割后最大子矩形的面积
思路:STL set。很容易想到,横纵坐标是相互独立的,最大子矩形面积一定产生于最大长度与最大宽度的乘积。因此我们只需要维护一个序列的最大值即可。对于二维可以直接当做一维来看,于是问题就变成了,需要在
的时间复杂度内,对一个序列完成下面三个操作: log n \log n
- 删除一个数
- 增加一个数(执行两次)
- 获取最大值
如何实现呢?我们需要有序记录每一个子线段的长度,并且子线段的长度可能重复,因此我们用
std::multiset来存储所有子线段的长度
- 使用
M.erase(M.find(value))实现:删除一个子线段长度值- 使用
M.insert(value)实现:增加子线段一个长度值- 使用
*M.rbegin()实现:获取当前所有子线段长度的最大值由于给的是切割的位置坐标
x,因此上述操作 1 不能直接实现,我们需要利用给定的切割坐标x计算出当前切割位置对应子线段的长度。如何实现呢?我们知道,对于当前切割的坐标x,对应的子线段的长度取决于当前切割坐标左右两个切割的位置rp, lp,因此我们只需要存储每一个切割的坐标即可。由于切割位置不会重复,并且需要在的时间复杂度内查询到,因此我们还是可以使用 log n \log n std::set来存储切割位置时间复杂度:
O ( n log n ) O(n \log n)
1 | |
【并查集】Milk Visits S
https://www.luogu.com.cn/problem/P5836
题意:给定一棵树,结点被标记成两种,一种是 H,一种是 G,在每一次查询中,需要知道指定的两个结点之间是否含有某一种标记
思路:对于树上标记,我们可以将相同颜色的分支连成一个连通块
- 如果查询的两个结点在同一个连通块,则查询两个结点所在的颜色与所需的颜色是否匹配即可
- 如果查询的两个结点不在同一个连通块,两个结点之间的路径一定是覆盖了两种颜色的标记,则答案一定是 1
时间复杂度:
Θ ( n + m ) \Theta(n+m)
1 | |
【并查集】尽量减少恶意软件的传播
https://leetcode.cn/problems/minimize-malware-spread/description/
题意:给定一个由邻接矩阵存储的无向图,其中某些结点具备感染能力,可以感染相连的所有结点,问消除哪一个结点的感染能力可以使得最终不被感染的结点数量尽可能少,给出消除的有感染能力的最小结点编号
思路:很显然我们可以将当前无向图的多个连通分量,共三种感染情况:
如果一个连通分量中含有
个感染结点,则当前连通分量一定会被全部感染; ≥ 2 \ge 2 如果一个连通块中含有
个感染结点,则无需任何操作; 0 0 如果一个连通块中含有
个感染结点,则最佳实践就是移除该连通块中唯一的那个感染结点。 1 1 当然了,由于只能移走一个感染结点,我们需要从所有只含有
个感染结点的连通块中移走连通块结点最多的那个感染结点。因此我们需要统计每一个连通分量中感染结点的数量以及总结点数,采用并查集进行统计。需要注意的是题目中的“索引最小”指的是结点编号最小而非结点在序列 1 1 中的下标最小。算法流程见代码。 i n i t i a l initial 时间复杂度:
O ( n 2 ) O(n^2)
1 | |
【并查集】账户合并
https://leetcode.cn/problems/accounts-merge/
题意:给定 n 个账户,每一个账户含有一个用户名和最多 m 个绑定的邮箱。由于一个用户可能注册多个账户,因此我们需要对所有的账户进行合并使得一个用户对应一个账户。合并的规则是将所有「含有相同邮箱的账户」视作同一个用户注册的账户。返回合并后的账户列表。
思路:这道题的需求很显然,我们需要合并含有相同邮箱的账户。显然有一个暴力的做法,我们直接枚举每一个账户中所有的邮箱,接着枚举剩余账户中的邮箱进行匹配,匹配上就进行合并,但这样做显然会造成大量的冗余匹配和冗余合并,我们不妨将这两个过程进行拆分。我们需要解决两个问题:
- 哪些账户需要合并?很容易想到并查集这样的数据结构。我们使用哈希表存储每一个邮箱的账户编号,最后进行集合合并即可维护好每一个账号归属的集合编号。
O ( n m ) O(nm) - 如何合并指定账户?对于上述维护好的集合编号,我们需要合并所有含有相同“祖先”的账户。排序去重或使用有序列表均可实现。
O ( n log n ) O(n\log n) 时间复杂度:
O ( n log n ) O(n\log n)
1 | |
1 | |
【树状数组】将元素分配到两个数组中 II
https://leetcode.cn/problems/distribute-elements-into-two-arrays-ii/description/
题意:给定
个数,现在需要将这些数按照某种规则分配到两个数组 n n 和 A A 中。初始化分配 B B nums[0]到中, A A nums[1]到中,接下来对于剩余的每个元素 B B nums[i],分配取决于和 A A 中比当前元素 B B nums[i]大的个数,最终返回两个分配好的数组思路:首先每一个元素都需要进行枚举,那么本题需要考虑的就是如何在
时间复杂度内统计出两数组中比当前元素大的元素个数。针对 C++ 和 Python 分别讨论 log \log
- C++
- 法一:
std::multiset<int>。可惜不行,因为统计比当前元素大的个数时,s.rbegin() - s.upper_bound(nums[i])是不合法的,因为std::multiset<int>的迭代器不是基于指针的,因此无法直接进行加减来计算地址差,遂作罢- 法二:树状数组。很容易想到利用前缀和统计比当前数大的数字个数,但是由于此处需要对前缀和进行单点修改,因此时间复杂度肯定会寄。有什么数据结构支持「单点修改,区间更新」呢?我们引入树状数组。我们将数组元素哈希到
[1, len(set(nums))]区间,定义哈希后的当前元素nums[i]为x,对于当前哈希后的x而言想要知道两个数组中有多少数比当前数严格大,只需要计算前缀和数组arr中arr[n] - arr[x]的结果即可- Python
SortedList。python 有一个sortedcontainers包其中有SortedList模块,可以实现std::multiset<int>所有操作并且可以进行随机下标访问,于是就可以进行下标访问 log \log 计算比当前数大的元素个数 O ( 1 ) O(1) - 题外话。LeetCode 可以进行第三方库导入的操作,某些比赛不允许,需要手搓
SortedList模块,当然可以用树状数组 or 线段树解决,板子链接:https://blog.dwj601.cn/Algorithm/a_template/#SortedList时间复杂度:
O ( n log n ) O(n \log n)
1 | |
1 | |
1 | |
【线段树/二分】以组为单位订音乐会的门票 🔥
https://leetcode.cn/problems/booking-concert-tickets-in-groups/
题意:给定一个长为
且初始值均为 n ≤ 5 × 1 0 4 n\le 5 \times 10^4 的数组 0 0 ,数组中的每个元素最多增加到 a a 。现在需要以这个数组为基础进行 m m 次询问,每次询问是以下两者之一: q ≤ 5 × 1 0 4 q\le 5 \times 10^4
- 给定一个
和 k k ,找到最小的 l i m lim 使得 i ∈ [ 0 , l i m ] i \in [0,lim] m − a i ≥ k m - a_i \ge k - 给定一个
和 k k ,找到最小的 l i m lim 使得 i ∈ [ 0 , l i m ] i \in [0,lim] m × ( i + 1 ) − ∑ j = 0 i a j ≥ k \displaystyle m\times (i+1) - \sum_{j=0}^i a_j \ge k 思路一:暴力。对于询问 1,我们直接顺序遍历 a 数组直到找到第一个符合条件的即可;对于询问 2,同样直接顺序遍历 a 数组直到找到第一个符合条件的即可。时间复杂度为
。 O ( q n ) O(qn) 思路二:线段树上二分。
暴力代码:
1 | |
线段树上二分代码:
1 | |
网瘾青年


技术栈
编程语言
开发工具
每当独自听着歌,或者看到一些人、一些场景时,脑海中总会有小人在低语,有时倒也能让自己受到启发。但很多想法转瞬即逝,故借此处将一些内容及时记录下来,权当留念。
网瘾青年


技术栈
编程语言
开发工具
每当独自听着歌,或者看到一些人、一些场景时,脑海中总会有小人在低语,有时倒也能让自己受到启发。但很多想法转瞬即逝,故借此处将一些内容及时记录下来,权当留念。