i127.topological_sort.md

拓扑排序 Topological Sorting

入度（In-degree）： 有向图（Directed Graph）中指向当前节点的点的个数（或指向当前节点的边的条数）

算法描述：

1. 统计每个点的入度

2. 将每个入度为 0 的点放入队列（Queue）中作为起始节点

3. 不断从队列中拿出一个点，去掉这个点的所有连边（指向其他点的边），其他点的相应的入度 - 1

4. 一旦发现新的入度为 0 的点，丢回队列中

拓扑排序并不是传统的排序算法 一个图可能存在多个拓扑序（Topological Order），也可能不存在任何拓扑序

拓扑排序的四种不同问法

• 1. 求任意一个拓扑序
• 2. 问是否存在拓扑序
  • 1中答案如果 长度等于所有节点个数 则存在，否则不存在。
• 3. 求是否存在且仅存在一个拓扑序
  • 如果过程中queue只有一个元素则只有一个拓扑序（因为只有一个选择。如果queue.size > 1 则不唯一
• 4. 求字典序最小的拓扑排序

---

i127 · Topological Sorting

Medium

https://www.lintcode.com/problem/127/

Description

Given an directed graph, a topological order of the graph nodes is defined as follow:

For each directed edge A -> B in graph, A must before B in the order list.
The first node in the order can be any node in the graph with no nodes direct to it.

Find any topological order for the given graph.

You can assume that there is at least one topological order in the graph.

The number of graph nodes <= 5000

Example

Example 1:

Input:

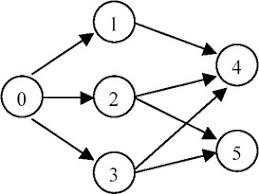
graph = {0,1,2,3#1,4#2,4,5#3,4,5#4#5}
Output:

[0, 1, 2, 3, 4, 5]
Explanation:

For graph as follow:

图片

he topological order can be:
[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]
...
You only need to return any topological order for the given graph.

Challenge

Can you do it in both BFS and DFS?

Tags

• Topological Sort
• Breadth First Search/BFS

Related Problems

• 815 Course Schedule IV Hard
• 615 Course Schedule Medium
• 616 Course Schedule II Medium
• 605 Sequence Reconstruction Medium

"""
class DirectedGraphNode:
     def __init__(self, x):
         self.label = x
         self.neighbors = []
"""

class Solution:
    """
    @param graph: A list of Directed graph node
    @return: Any topological order for the given graph.
    """
    def topSort(self, graph):
        # write your code here
        node2indegreeDict = self.get_indegree(graph)

        # bfs
        topoorder = []
        # start with 0-indegree nodes
        startnodes = [node for node in graph if node2indegreeDict[node] == 0]
        queue = collections.deque(startnodes)
        while queue:
            currnode = queue.popleft()
            topoorder.append(currnode)
            for neighbor in currnode.neighbors:
                node2indegreeDict[neighbor] -= 1
                if node2indegreeDict[neighbor] == 0:
                    queue.append(neighbor)
        return topoorder

    def get_indegree(self, graph):
        # initialize the dict containing all nodes
        node2indegreeDict = {node:0 for node in graph}
        # count indegree for each node
        for node in graph:
            for neighbor in node.neighbors:
                node2indegreeDict[neighbor] += 1
        return  node2indegreeDict