'Computer Science' is fundamentally problem solving.
Problem solving can be thought as the process of taking some input (a problem we want to solve) and generate some output (the solution to our problem).
To begin doing that, we'll need a way to represent inputs and outputs, so we can store and work with information in a standardized way.
Unary - the system where each digit represents a single value.
Decimal - the system which uses ten digits (0 to 9) to count to higher numbers.
Binary - the system computers use. It has only two digits (0 & 1).
-
to represent 0 in binary:
0 0 0 -
to represent 1 in binary:
0 0 1 -
to represent 2 in binary, we'll need to change another digit:
0 1 0 -
to represent 3, we'll add 1:
0 1 1 -
to represent 4:
1 0 0 -
to represent 5:
1 0 1 -
to represent 6:
1 1 0 -
to represent 7:
1 1 1
Each binary digit is also called a bit. Since computers run on electricity, which can be turned on or off, we can simply represent a bit by turning some switch on or off to represent a 0 or a 1.
Inside modern computers, there a billions of tiny switches called transistors that can be turned on and off to represent different values.
The pattern to count in binary with multiple bits is the same as the pattern in decimal with multiple digits. For example, we know the following number in decimal represents one hundred and twenty-three.
1 2 3
The 3 is in the ones place, the 2 is in the tens place, and the 1 is in the hundreds place.
So 123 is 100×1 + 10×2 + 1×3 = 100 + 20 + 3 = 123.
To count higher than 7, we would need another bit to the left to represent the number 8. Most computers use 8 bits at a time, like 00000011 for the number 3.
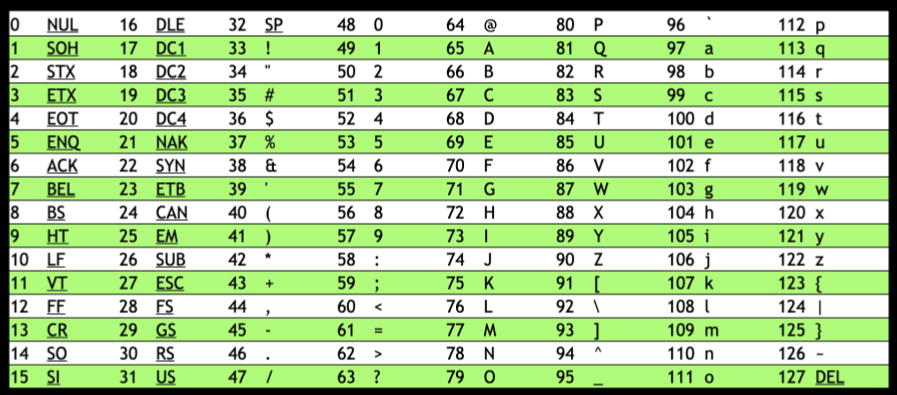
There's a standard mapping of numbers to letters called ASCII (American Standard Code for Information Interchange), which also includes lowercase letters and punctuations.
Expanded map of ASCII values:
- to represent "A", the number is 65, and in binary:
0 1 0 0 0 0 0 1
- to represent "B", the number is 66, and in binary:
0 1 0 0 0 0 1 0
- and so on.
Other characters, such as letters with accent marks, symbols, are part of a standard called Unicode, which uses more than 8 bits for each character, that ASCII uses.
When we receive an emoji, our computer is actually reveiving a number in binary that it then maps to the image of the emoji based on the Unicode standard. Also worth noting, companies that create software for their devices will have slightly different images that represent each emoji, because only the descriptions were standardized.
With bits, we can map numbers to colors as well. There are many different systems to represent colors, but a common one is RGB, which represents colors by indicating the amount of red, green and blue within each color.
-
The little squares on screens are called pixels, which combined make images.
-
Videos are sequences of images, changing multiple times a second to give us the appearance of motion.
-
Music can be represented by bits too. MIDI is one such format which represents music with numbers for each of the notes and their duration & volume.
All of these ideas are just zeroes and ones, interpreted and used by software we've written to interpret them in the ways that we want.